Computational complexity of mathematical operations

From HandWiki
Short description: Algorithmic runtime requirements for common math procedures
Graphs of functions commonly used in the analysis of algorithms, showing the number of operations [math]\displaystyle{ N }[/math] versus input size [math]\displaystyle{ n }[/math] for each function

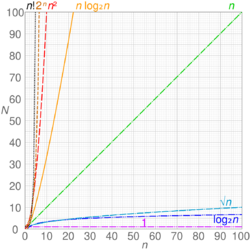
The following tables list the computational complexity of various algorithms for common mathematical operations.

Here, complexity refers to the time complexity of performing computations on a multitape Turing machine.[1] See big O notation for an explanation of the notation used.

Note: Due to the variety of multiplication algorithms, [math]\displaystyle{ M(n) }[/math] below stands in for the complexity of the chosen multiplication algorithm.

Arithmetic functions

This table lists the complexity of mathematical operations on integers.

Operation Input Output Algorithm Complexity
Addition Two [math]\displaystyle{ n }[/math]-digit numbers One [math]\displaystyle{ n+1 }[/math]-digit number Schoolbook addition with carry [math]\displaystyle{ \Theta(n) }[/math]
Subtraction Two [math]\displaystyle{ n }[/math]-digit numbers One [math]\displaystyle{ n+1 }[/math]-digit number Schoolbook subtraction with borrow [math]\displaystyle{ \Theta(n) }[/math]
Multiplication Two [math]\displaystyle{ n }[/math]-digit numbers
 One [math]\displaystyle{ 2n }[/math]-digit number Schoolbook long multiplication [math]\displaystyle{ O\mathord\left(n^{2}\right) }[/math]
Karatsuba algorithm [math]\displaystyle{ O\mathord\left(n^{1.585}\right) }[/math]
3-way Toom–Cook multiplication [math]\displaystyle{ O\mathord\left(n^{1.465}\right) }[/math]
[math]\displaystyle{ k }[/math]-way Toom–Cook multiplication [math]\displaystyle{ O\mathord\left(n^{\frac{\log(2k - 1)}{\log k}}\right) }[/math]
Mixed-level Toom–Cook (Knuth 4.3.3-T)[2] [math]\displaystyle{ O\mathord\left(n \, 2^{\sqrt{2 \log n}} \, \log n\right) }[/math]
Schönhage–Strassen algorithm [math]\displaystyle{ O\mathord\left(n \log n \log \log n\right) }[/math]
Harvey-Hoeven algorithm[3][4] [math]\displaystyle{ O(n \log n) }[/math]
Division Two [math]\displaystyle{ n }[/math]-digit numbers One [math]\displaystyle{ n }[/math]-digit number Schoolbook long division [math]\displaystyle{ O\mathord\left(n^{2}\right) }[/math]
Burnikel–Ziegler Divide-and-Conquer Division[5] [math]\displaystyle{ O(M(n) \log n) }[/math]
Newton–Raphson division [math]\displaystyle{ O(M(n)) }[/math]
Square root One [math]\displaystyle{ n }[/math]-digit number One [math]\displaystyle{ n }[/math]-digit number Newton's method [math]\displaystyle{ O(M(n)) }[/math]
Modular exponentiation Two [math]\displaystyle{ n }[/math]-digit integers and a [math]\displaystyle{ k }[/math]-bit exponent One [math]\displaystyle{ n }[/math]-digit integer Repeated multiplication and reduction [math]\displaystyle{ O\mathord\left(M(n) \, 2^{k}\right) }[/math]
Exponentiation by squaring [math]\displaystyle{ O(M(n) \, k) }[/math]
Exponentiation with Montgomery reduction [math]\displaystyle{ O(M(n) \, k) }[/math]

On stronger computational models, specifically a pointer machine and consequently also a unit-cost random-access machine it is possible to multiply two n-bit numbers in time O(n).[6]

Algebraic functions

Here we consider operations over polynomials and n denotes their degree; for the coefficients we use a unit-cost model, ignoring the number of bits in a number. In practice this means that we assume them to be machine integers.

Operation Input Output Algorithm Complexity
Polynomial evaluation One polynomial of degree [math]\displaystyle{ n }[/math] with integer coefficients One number Direct evaluation [math]\displaystyle{ \Theta(n) }[/math]
Horner's method [math]\displaystyle{ \Theta(n) }[/math]
Polynomial gcd (over [math]\displaystyle{ \mathbb{Z}[x] }[/math] or [math]\displaystyle{ F[x] }[/math]) Two polynomials of degree [math]\displaystyle{ n }[/math] with integer coefficients One polynomial of degree at most [math]\displaystyle{ n }[/math] Euclidean algorithm [math]\displaystyle{ O\mathord\left(n^{2}\right) }[/math]
Fast Euclidean algorithm (Lehmer)[citation needed] [math]\displaystyle{ O(M(n) \log n) }[/math]

Special functions

Many of the methods in this section are given in Borwein & Borwein.[7]

Elementary functions

The elementary functions are constructed by composing arithmetic operations, the exponential function ([math]\displaystyle{ \exp }[/math]), the natural logarithm ([math]\displaystyle{ \log }[/math]), trigonometric functions ([math]\displaystyle{ \sin, \cos }[/math]), and their inverses. The complexity of an elementary function is equivalent to that of its inverse, since all elementary functions are analytic and hence invertible by means of Newton's method. In particular, if either [math]\displaystyle{ \exp }[/math] or [math]\displaystyle{ \log }[/math] in the complex domain can be computed with some complexity, then that complexity is attainable for all other elementary functions.

Below, the size [math]\displaystyle{ n }[/math] refers to the number of digits of precision at which the function is to be evaluated.

Algorithm Applicability Complexity
Taylor series; repeated argument reduction (e.g. [math]\displaystyle{ \exp(2x) = [\exp(x)]^2 }[/math]) and direct summation [math]\displaystyle{ \exp, \log, \sin, \cos, \arctan }[/math] [math]\displaystyle{ O\mathord\left(M(n) n^{1/2}\right) }[/math]
Taylor series; FFT-based acceleration [math]\displaystyle{ \exp, \log, \sin, \cos, \arctan }[/math] [math]\displaystyle{ O\mathord\left(M(n) n^{1/3} (\log n)^2\right) }[/math]
Taylor series; binary splitting + bit-burst algorithm[8] [math]\displaystyle{ \exp, \log, \sin, \cos, \arctan }[/math] [math]\displaystyle{ O\mathord\left(M(n) (\log n)^2\right) }[/math]
Arithmetic–geometric mean iteration[9] [math]\displaystyle{ \exp, \log, \sin, \cos, \arctan }[/math] [math]\displaystyle{ O(M(n) \log n) }[/math]

It is not known whether [math]\displaystyle{ O(M(n) \log n) }[/math] is the optimal complexity for elementary functions. The best known lower bound is the trivial bound [math]\displaystyle{ \Omega }[/math][math]\displaystyle{ (M(n)) }[/math].

Non-elementary functions

Function Input Algorithm Complexity
Gamma function [math]\displaystyle{ n }[/math]-digit number Series approximation of the incomplete gamma function [math]\displaystyle{ O\mathord\left(M(n) n^{1/2} (\log n)^2\right) }[/math]
Fixed rational number Hypergeometric series [math]\displaystyle{ O\mathord\left(M(n) (\log n)^2\right) }[/math]
[math]\displaystyle{ m/24 }[/math], for [math]\displaystyle{ m }[/math] integer. Arithmetic-geometric mean iteration [math]\displaystyle{ O(M(n) \log n) }[/math]
Hypergeometric function [math]\displaystyle{ {}_p\!F_q }[/math] [math]\displaystyle{ n }[/math]-digit number (As described in Borwein & Borwein) [math]\displaystyle{ O\mathord\left(M(n) n^{1/2} (\log n)^2\right) }[/math]
Fixed rational number Hypergeometric series [math]\displaystyle{ O\mathord\left(M(n) (\log n)^2\right) }[/math]

Mathematical constants

This table gives the complexity of computing approximations to the given constants to [math]\displaystyle{ n }[/math] correct digits.

Constant Algorithm Complexity
Golden ratio, [math]\displaystyle{ \phi }[/math] Newton's method [math]\displaystyle{ O(M(n)) }[/math]
Square root of 2, [math]\displaystyle{ \sqrt{2} }[/math] Newton's method [math]\displaystyle{ O(M(n)) }[/math]
Euler's number, [math]\displaystyle{ e }[/math] Binary splitting of the Taylor series for the exponential function [math]\displaystyle{ O(M(n) \log n) }[/math]
Newton inversion of the natural logarithm [math]\displaystyle{ O(M(n) \log n) }[/math]
Pi, [math]\displaystyle{ \pi }[/math] Binary splitting of the arctan series in Machin's formula [math]\displaystyle{ O\mathord\left(M(n) (\log n)^2\right) }[/math][10]
Gauss–Legendre algorithm [math]\displaystyle{ O(M(n) \log n) }[/math][10]
Euler's constant, [math]\displaystyle{ \gamma }[/math] Sweeney's method (approximation in terms of the exponential integral) [math]\displaystyle{ O\mathord\left(M(n) (\log n)^2\right) }[/math]

Number theory

Algorithms for number theoretical calculations are studied in computational number theory.

Operation Input Output Algorithm Complexity
Greatest common divisor Two [math]\displaystyle{ n }[/math]-digit integers One integer with at most [math]\displaystyle{ n }[/math] digits Euclidean algorithm [math]\displaystyle{ O\mathord\left(n^{2}\right) }[/math]
Binary GCD algorithm [math]\displaystyle{ O\mathord\left(n^2\right) }[/math]
Left/right k-ary binary GCD algorithm[11] [math]\displaystyle{ O\mathord\left(\frac{n^{2}}{\log n}\right) }[/math]
Stehlé–Zimmermann algorithm[12] [math]\displaystyle{ O(M(n) \log n) }[/math]
Schönhage controlled Euclidean descent algorithm[13] [math]\displaystyle{ O(M(n) \log n) }[/math]
Jacobi symbol Two [math]\displaystyle{ n }[/math]-digit integers [math]\displaystyle{ 0 }[/math], [math]\displaystyle{ -1 }[/math] or [math]\displaystyle{ 1 }[/math] Schönhage controlled Euclidean descent algorithm[14] [math]\displaystyle{ O(M(n) \log n) }[/math]
Stehlé–Zimmermann algorithm[15] [math]\displaystyle{ O(M(n) \log n) }[/math]
Factorial A positive integer less than [math]\displaystyle{ m }[/math] One [math]\displaystyle{ O(m \log m) }[/math]-digit integer Bottom-up multiplication [math]\displaystyle{ O\mathord\left(M\left(m^2\right) \log m\right) }[/math]
Binary splitting [math]\displaystyle{ O(M(m \log m) \log m) }[/math]
Exponentiation of the prime factors of [math]\displaystyle{ m }[/math] [math]\displaystyle{ O(M(m \log m) \log \log m) }[/math],[16]
[math]\displaystyle{ O(M(m \log m)) }[/math][1]
Primality test A [math]\displaystyle{ n }[/math]-digit integer True or false AKS primality test
Elliptic curve primality proving [math]\displaystyle{ O\mathord\left(n^{4+\varepsilon}\right) }[/math] heuristically[17]
Baillie–PSW primality test
Miller–Rabin primality test [math]\displaystyle{ O\mathord\left(kn^{2+\varepsilon}\right) }[/math][18]
Solovay–Strassen primality test [math]\displaystyle{ O\mathord\left(kn^{2+\varepsilon}\right) }[/math][18]
Integer factorization A [math]\displaystyle{ b }[/math]-bit input integer A set of factors General number field sieve [math]\displaystyle{ O\mathord\left((1+\varepsilon)^b\right) }[/math][nb 1]
Shor's algorithm [math]\displaystyle{ O(M(b) b) }[/math], on a quantum computer

Matrix algebra

Main page: Computational complexity of matrix multiplication

The following complexity figures assume that arithmetic with individual elements has complexity O(1), as is the case with fixed-precision floating-point arithmetic or operations on a finite field.

Operation Input Output Algorithm Complexity
Matrix multiplication Two [math]\displaystyle{ n \times n }[/math] matrices One [math]\displaystyle{ n \times n }[/math] matrix Schoolbook matrix multiplication [math]\displaystyle{ O(n^{3}) }[/math]
Strassen algorithm [math]\displaystyle{ O\mathord\left(n^{2.807}\right) }[/math]
Coppersmith–Winograd algorithm (galactic algorithm) [math]\displaystyle{ O\mathord\left(n^{2.376}\right) }[/math]
Optimized CW-like algorithms[19][20][21][22] (galactic algorithms) [math]\displaystyle{ O\mathord\left(n^{2.3728596}\right) }[/math]
Matrix multiplication One [math]\displaystyle{ n \times m }[/math] matrix, and
one [math]\displaystyle{ m \times p }[/math] matrix 		One [math]\displaystyle{ n \times p }[/math] matrix Schoolbook matrix multiplication [math]\displaystyle{ O(nmp) }[/math]
Matrix multiplication One [math]\displaystyle{ n \times \left\lceil n^k \right\rceil }[/math] matrix, and
one [math]\displaystyle{ \left\lceil n^k \right\rceil \times n }[/math] matrix, for some [math]\displaystyle{ k \geq 0 }[/math] 		One [math]\displaystyle{ n \times n }[/math] matrix Algorithms given in [23] [math]\displaystyle{ O(n^{\omega(k)+\epsilon}) }[/math], where upper bounds on [math]\displaystyle{ \omega(k) }[/math] are given in [23]
Matrix inversion One [math]\displaystyle{ n \times n }[/math] matrix One [math]\displaystyle{ n \times n }[/math] matrix Gauss–Jordan elimination [math]\displaystyle{ O\mathord\left(n^{3}\right) }[/math]
Strassen algorithm [math]\displaystyle{ O\mathord\left(n^{2.807}\right) }[/math]
Coppersmith–Winograd algorithm [math]\displaystyle{ O\mathord\left(n^{2.376}\right) }[/math]
Optimized CW-like algorithms [math]\displaystyle{ O\mathord\left(n^{2.373}\right) }[/math]
Singular value decomposition One [math]\displaystyle{ m \times n }[/math] matrix One [math]\displaystyle{ m \times m }[/math] matrix,
one [math]\displaystyle{ m \times n }[/math] matrix, &
one [math]\displaystyle{ n \times n }[/math] matrix 		Bidiagonalization and QR algorithm [math]\displaystyle{ O\mathord\left(m^{2}n\right) }[/math]
([math]\displaystyle{ m \geq n }[/math])
One [math]\displaystyle{ m\times n }[/math] matrix,
one [math]\displaystyle{ n \times n }[/math] matrix, &
one [math]\displaystyle{ n \times n }[/math] matrix 		Bidiagonalization and QR algorithm [math]\displaystyle{ O\mathord\left(mn^{2}\right) }[/math]
([math]\displaystyle{ m \leq n }[/math])
Determinant One [math]\displaystyle{ n \times n }[/math] matrix One number Laplace expansion [math]\displaystyle{ O(n!) }[/math]
Division-free algorithm[24] [math]\displaystyle{ O\mathord\left(n^{4}\right) }[/math]
LU decomposition [math]\displaystyle{ O(n^{3}) }[/math]
Bareiss algorithm [math]\displaystyle{ O\mathord\left(n^3\right) }[/math]
[math]\displaystyle{ O\mathord\left(n^{2.373}\right) }[/math]
Back substitution Triangular matrix [math]\displaystyle{ n }[/math] solutions Back substitution[25] [math]\displaystyle{ O\mathord\left(n^2\right) }[/math]

In 2005, Henry Cohn, Robert Kleinberg, Balázs Szegedy, and Chris Umans showed that either of two different conjectures would imply that the exponent of matrix multiplication is 2.[26]

Transforms

Algorithms for computing transforms of functions (particularly integral transforms) are widely used in all areas of mathematics, particularly analysis and signal processing.

Operation Input Output Algorithm Complexity
Discrete Fourier transform Finite data sequence of size [math]\displaystyle{ n }[/math] Set of complex numbers Schoolbook [math]\displaystyle{ O(n^2) }[/math]
Fast Fourier transform [math]\displaystyle{ O(n \log n) }[/math]

Notes

  1. ↑ This form of sub-exponential time is valid for all [math]\displaystyle{ \varepsilon \gt 0 }[/math]. A more precise form of the complexity can be given as [math]\displaystyle{ O\mathord\left(\exp\sqrt[3]{\frac{64}{9} b (\log b)^2}\right). }[/math]

References

  1. ↑ 1.0 1.1 Schönhage, A.; Grotefeld, A.F.W.; Vetter, E. (1994). Fast Algorithms—A Multitape Turing Machine Implementation. BI Wissenschafts-Verlag. ISBN 978-3-411-16891-0. OCLC 897602049. 
  2. ↑ Knuth 1997
  3. ↑ Harvey, D.; Van Der Hoeven, J. (2021). "Integer multiplication in time O (n log n)". Annals of Mathematics 193 (2): 563–617. doi:10.4007/annals.2021.193.2.4. https://hal.archives-ouvertes.fr/hal-02070778v2/file/nlogn.pdf. 
  4. ↑ Klarreich, Erica (December 2019). "Multiplication hits the speed limit". Commun. ACM 63 (1): 11–13. doi:10.1145/3371387. 
  5. ↑ Burnikel, Christoph; Ziegler, Joachim (1998). Fast Recursive Division. Forschungsberichte des Max-Planck-Instituts für Informatik. Saarbrücken: MPI Informatik Bibliothek & Dokumentation. MPII-98-1-022. OCLC 246319574. 
  6. ↑ Schönhage, Arnold (1980). "Storage Modification Machines". SIAM Journal on Computing 9 (3): 490–508. doi:10.1137/0209036. 
  7. ↑ Borwein, J.; Borwein, P. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity. Wiley. ISBN 978-0-471-83138-9. OCLC 755165897. 
  8. ↑ Chudnovsky, David; Chudnovsky, Gregory (1988). "Approximations and complex multiplication according to Ramanujan". Ramanujan revisited: Proceedings of the Centenary Conference. Academic Press. pp. 375–472. ISBN 978-0-01-205856-5. 
  9. ↑ Brent, Richard P. (2014). "Multiple-precision zero-finding methods and the complexity of elementary function evaluation". in Traub, J.F.. Analytic Computational Complexity. Elsevier. pp. 151–176. ISBN 978-1-4832-5789-1. https://books.google.com/books?id=UZriBQAAQBAJ&pg=PA151. 
  10. ↑ 10.0 10.1 Richard P. Brent (2020), The Borwein Brothers, Pi and the AGM, Springer Proceedings in Mathematics & Statistics, 313, doi:10.1007/978-3-030-36568-4, ISBN 978-3-030-36567-7 
  11. ↑ Sorenson, J. (1994). "Two Fast GCD Algorithms". Journal of Algorithms 16 (1): 110–144. doi:10.1006/jagm.1994.1006. 
  12. ↑ Crandall, R.; Pomerance, C. (2005). "Algorithm 9.4.7 (Stehlé-Zimmerman binary-recursive-gcd)". Prime Numbers – A Computational Perspective (2nd ed.). Springer. pp. 471–3. ISBN 978-0-387-28979-3. https://books.google.com/books?id=ZXjHKPS1LEAC&pg=PA471. 
  13. ↑ Möller N (2008). "On Schönhage's algorithm and subquadratic integer gcd computation". Mathematics of Computation 77 (261): 589–607. doi:10.1090/S0025-5718-07-02017-0. Bibcode: 2008MaCom..77..589M. http://www.lysator.liu.se/~nisse/archive/sgcd.pdf. 
  14. ↑ Bernstein, D.J.. "Faster Algorithms to Find Non-squares Modulo Worst-case Integers". http://cr.yp.to/papers/nonsquare.ps. 
  15. ↑ Brent, Richard P.; Zimmermann, Paul (2010). "An [math]\displaystyle{ O(M(n) \log n) }[/math] algorithm for the Jacobi symbol". International Algorithmic Number Theory Symposium. Springer. pp. 83–95. doi:10.1007/978-3-642-14518-6_10. ISBN 978-3-642-14518-6. https://link.springer.com/chapter/10.1007/978-3-642-14518-6_10. 
  16. ↑ Borwein, P. (1985). "On the complexity of calculating factorials". Journal of Algorithms 6 (3): 376–380. doi:10.1016/0196-6774(85)90006-9. 
  17. ↑ Morain, F. (2007). "Implementing the asymptotically fast version of the elliptic curve primality proving algorithm". Mathematics of Computation 76 (257): 493–505. doi:10.1090/S0025-5718-06-01890-4. Bibcode: 2007MaCom..76..493M. 
  18. ↑ 18.0 18.1 Monier, Louis (1980). "Evaluation and comparison of two efficient probabilistic primality testing algorithms". Theoretical Computer Science 12 (1): 97–108. doi:10.1016/0304-3975(80)90007-9. 
  19. ↑ Alman, Josh; Williams, Virginia Vassilevska (2020), "A Refined Laser Method and Faster Matrix Multiplication", 32nd Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2021), doi:10.1137/1.9781611976465.32, https://www.siam.org/conferences/cm/program/accepted-papers/soda21-accepted-papers 
  20. ↑ Davie, A.M.; Stothers, A.J. (2013), "Improved bound for complexity of matrix multiplication", Proceedings of the Royal Society of Edinburgh 143A (2): 351–370, doi:10.1017/S0308210511001648 
  21. ↑ Vassilevska Williams, Virginia (2014), Breaking the Coppersmith-Winograd barrier: Multiplying matrices in O(n2.373) time, https://www.scribd.com/document/397495001/Breaking-the-Coppersmith-Winograd-Barrier-for-Matrix-Multiplication-Algorithms 
  22. ↑ Le Gall, François (2014), "Powers of tensors and fast matrix multiplication", Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation — ISSAC '14, p. 23, doi:10.1145/2608628.2627493, ISBN 9781450325011, Bibcode: 2014arXiv1401.7714L 
  23. ↑ 23.0 23.1 Le Gall, François; Urrutia, Floren (2018). "Improved Rectangular Matrix Multiplication using Powers of the Coppersmith-Winograd Tensor". in Czumaj, Artur. Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics (SIAM). doi:10.1137/1.9781611975031.67. ISBN 978-1-61197-503-1. 
  24. ↑ Rote, G. (2001). "Division-free algorithms for the determinant and the pfaffian: algebraic and combinatorial approaches". Computational discrete mathematics. Springer. pp. 119–135. ISBN 3-540-45506-X. http://page.mi.fu-berlin.de/rote/Papers/pdf/Division-free+algorithms.pdf. 
  25. ↑ Fraleigh, J.B.; Beauregard, R.A. (1987). Linear Algebra (3rd ed.). Addison-Wesley. pp. 95. ISBN 978-0-201-15459-7. 
  26. ↑ Cohn, Henry; Kleinberg, Robert; Szegedy, Balazs; Umans, Chris (2005). "Group-theoretic Algorithms for Matrix Multiplication". Proceedings of the 46th Annual Symposium on Foundations of Computer Science. IEEE. pp. 379–388. doi:10.1109/SFCS.2005.39. ISBN 0-7695-2468-0. 

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Computational_complexity_of_mathematical_operations&oldid=3360408"