Converse implication
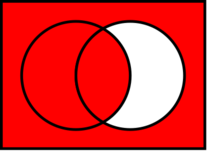
(the white area shows where the statement is false)
Converse implication is the converse of implication, written ←. That is to say; that for any two propositions [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math], if [math]\displaystyle{ Q }[/math] implies [math]\displaystyle{ P }[/math], then [math]\displaystyle{ P }[/math] is the converse implication of [math]\displaystyle{ Q }[/math].
It is written [math]\displaystyle{ P \leftarrow Q }[/math], but may also be notated [math]\displaystyle{ P \subset Q }[/math], or "Bpq" (in Bocheński notation).
Definition
Truth table
The truth table of [math]\displaystyle{ P \leftarrow Q }[/math]
| [math]\displaystyle{ P }[/math] | [math]\displaystyle{ Q }[/math] | [math]\displaystyle{ P \leftarrow Q }[/math] |
| T | T | T |
| T | F | T |
| F | T | F |
| F | F | T |
Logical Equivalences
Converse implication is logically equivalent to the disjunction of [math]\displaystyle{ P }[/math] and [math]\displaystyle{ \neg Q }[/math]
| [math]\displaystyle{ P \leftarrow Q }[/math] | [math]\displaystyle{ \Leftrightarrow }[/math] | [math]\displaystyle{ P }[/math] | [math]\displaystyle{ \or }[/math] | [math]\displaystyle{ \neg Q }[/math] |
|
|
[math]\displaystyle{ \Leftrightarrow }[/math] | 
|
[math]\displaystyle{ \or }[/math] | 
|
Properties
truth-preserving: The interpretation under which all variables are assigned a truth value of 'true' produces a truth value of 'true' as a result of converse implication.
Symbol
←, ⇐
Natural language
"Not q without p."
"p if q."
See also
External links
 | ||
| ||
| ||
| ||
| ||
 |
