Converse nonimplication

Short description: Logical connective

Venn diagram of $P\nleftarrow Q$
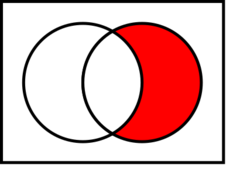
(the red area is true)

In logic, converse nonimplication is a logical connective which is the negation of converse implication (equivalently, the negation of the converse of implication).

Definition

Converse nonimplication is notated $P\nleftarrow Q$, or $P\subset ̸Q$, and is logically equivalent to $\mathrm{\neg }(P\leftarrow Q)$ and $\mathrm{\neg }P\wedge Q$.

Truth table

The truth table of $P\nleftarrow Q$.

$P$	$Q$	$P\nleftarrow Q$
True	True	False
True	False	False
False	True	True
False	False	False

Notation

Converse nonimplication is notated $p\nleftarrow q$, which is the left arrow from converse implication ($\leftarrow$), negated with a stroke (/).

Alternatives include

• $p\subset ̸q$, which combines converse implication's $\subset$, negated with a stroke (/).
• $p\tilde{\leftarrow }q$, which combines converse implication's left arrow ($\leftarrow$) with negation's tilde ($\sim$).
• Mpq, in Bocheński notation

Properties

falsehood-preserving: The interpretation under which all variables are assigned a truth value of 'false' produces a truth value of 'false' as a result of converse nonimplication

Natural language

Grammatical

Example,

If it rains (P) then I get wet (Q), just because I am wet (Q) does not mean it is raining, in reality I went to a pool party with the co-ed staff, in my clothes (~P) and that is why I am facilitating this lecture in this state (Q).

Rhetorical

Q does not imply P.

Boolean algebra

Converse Nonimplication in a general Boolean algebra is defined as $q\nleftarrow p=q^{\prime }p$.

Example of a 2-element Boolean algebra: the 2 elements {0,1} with 0 as zero and 1 as unity element, operators $\sim$ as complement operator, $\vee$ as join operator and $\wedge$ as meet operator, build the Boolean algebra of propositional logic.

$\sim x$ 1 0 x 0 1	and	y 1 1 1 0 0 1 $y_{\vee }x$ 0 1 x	and	y 1 0 1 0 0 0 $y_{\wedge }x$ 0 1 x	then $y\nleftarrow x$ means	y 1 0 0 0 0 1 $y\nleftarrow x$ 0 1 x
(Negation)		(Inclusive or)		(And)		(Converse nonimplication)

Example of a 4-element Boolean algebra: the 4 divisors {1,2,3,6} of 6 with 1 as zero and 6 as unity element, operators ${}^c$ (co-divisor of 6) as complement operator, ${}_{\vee }$ (least common multiple) as join operator and ${}_{\wedge }$ (greatest common divisor) as meet operator, build a Boolean algebra.

$x^c$ 6 3 2 1 x 1 2 3 6	and	y 6 6 6 6 6 3 3 6 3 6 2 2 2 6 6 1 1 2 3 6 $y_{\vee }x$ 1 2 3 6 x	and	y 6 1 2 3 6 3 1 1 3 3 2 1 2 1 2 1 1 1 1 1 $y_{\wedge }x$ 1 2 3 6 x	then $y\nleftarrow x$ means	y 6 1 1 1 1 3 1 2 1 2 2 1 1 3 3 1 1 2 3 6 $y\nleftarrow x$ 1 2 3 6 x
(Co-divisor 6)		(Least common multiple)		(Greatest common divisor)		(x's greatest divisor coprime with y)

Properties

Non-associative

$r\nleftarrow (q\nleftarrow p)=(r\nleftarrow q)\nleftarrow p$ if and only if $rp=0$ #s5 (In a two-element Boolean algebra the latter condition is reduced to $r=0$ or $p=0$). Hence in a nontrivial Boolean algebra Converse Nonimplication is nonassociative. $$\begin{array}{rlr}(r\nleftarrow q)\nleftarrow p& =r^{\prime }q\nleftarrow p& \text{(by definition)}\\ & =(r^{\prime }q{)}^{\prime }p& \text{(by definition)}\\ & =(r+q^{\prime })p& \text{(De Morgan's laws)}\\ & =(r+r^{\prime }{q}^{\prime })p& \text{(Absorption law)}\\ & =rp+r^{\prime }{q}^{\prime }p\\ & =rp+r^{\prime }(q\nleftarrow p)& \text{(by definition)}\\ & =rp+r\nleftarrow (q\nleftarrow p)& \text{(by definition)}\\ \end{array}$$

Clearly, it is associative if and only if $rp=0$.

Non-commutative

• $q\nleftarrow p=p\nleftarrow q$ if and only if $q=p$ #s6. Hence Converse Nonimplication is noncommutative.

Neutral and absorbing elements

• 0 is a left neutral element ($0\nleftarrow p=p$) and a right absorbing element ($p\nleftarrow 0=0$).
• $1\nleftarrow p=0$, $p\nleftarrow 1=p^{\prime }$, and $p\nleftarrow p=0$.
• Implication $q\to p$ is the dual of converse nonimplication $q\nleftarrow p$ #s7.

Converse Nonimplication is noncommutative
Step	Make use of	Resulting in
s.1	Definition	$q\tilde{\leftarrow }p=q^{\prime }p$
s.2	Definition	$p\tilde{\leftarrow }q=p^{\prime }q$
s.3	s.1 s.2	$q\tilde{\leftarrow }p=p\tilde{\leftarrow }q\iff q^{\prime }p=q{p}^{\prime }$
s.4		$q$	$=$	$q.1$
s.5	s.4.right - expand Unit element		$=$	$q.(p+p^{\prime })$
s.6	s.5.right - evaluate expression		$=$	$qp+q{p}^{\prime }$
s.7	s.4.left = s.6.right	$q=qp+q{p}^{\prime }$
s.8		$q^{\prime }p=q{p}^{\prime }$	$\Rightarrow$	$qp+q{p}^{\prime }=qp+q^{\prime }p$
s.9	s.8 - regroup common factors		$\Rightarrow$	$q.(p+p^{\prime })=(q+q^{\prime }).p$
s.10	s.9 - join of complements equals unity		$\Rightarrow$	$q.1=1.p$
s.11	s.10.right - evaluate expression		$\Rightarrow$	$q=p$
s.12	s.8 s.11	$q^{\prime }p=q{p}^{\prime }\Rightarrow q=p$
s.13		$q=p\Rightarrow q^{\prime }p=q{p}^{\prime }$
s.14	s.12 s.13	$q=p\iff q^{\prime }p=q{p}^{\prime }$
s.15	s.3 s.14	$q\tilde{\leftarrow }p=p\tilde{\leftarrow }q\iff q=p$

Implication is the dual of Converse Nonimplication
Step	Make use of	Resulting in
s.1	Definition	$\mathrm{dual}(q\tilde{\leftarrow }p)$	$=$	$\mathrm{dual}(q^{\prime }p)$
s.2	s.1.right - .'s dual is +		$=$	$q^{\prime }+p$
s.3	s.2.right - Involution complement		$=$	$(q^{\prime }+p{)}^{″}$
s.4	s.3.right - De Morgan's laws applied once		$=$	$(q{p}^{\prime }{)}^{\prime }$
s.5	s.4.right - Commutative law		$=$	$(p^{\prime }q{)}^{\prime }$
s.6	s.5.right		$=$	$(p\tilde{\leftarrow }q{)}^{\prime }$
s.7	s.6.right		$=$	$p\leftarrow q$
s.8	s.7.right		$=$	$q\to p$
s.9	s.1.left = s.8.right	$\mathrm{dual}(q\tilde{\leftarrow }p)=q\to p$

Computer science

An example for converse nonimplication in computer science can be found when performing a right outer join on a set of tables from a database, if records not matching the join-condition from the "left" table are being excluded.

References

• Knuth, Donald E. (2011). The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1 (1st ed.). Addison-Wesley Professional. ISBN 978-0-201-03804-0.