Sheffer stroke

From HandWiki
Short description: Logical operation

Sheffer stroke
NAND
Venn diagram of Sheffer stroke
Definition[math]\displaystyle{ \overline{x \cdot y} }[/math]
Truth table[math]\displaystyle{ (0111) }[/math]
Logic gateNAND ANSI.svg
Normal forms
Disjunctive[math]\displaystyle{ \overline{x} + \overline{y} }[/math]
Conjunctive[math]\displaystyle{ \overline{x} + \overline{y} }[/math]
Zhegalkin polynomial[math]\displaystyle{ 1 \oplus xy }[/math]
white;">Post's lattices
0-preservingno
1-preservingno
Monotoneno
Affineno

In Boolean functions and propositional calculus, the Sheffer stroke denotes a logical operation that is equivalent to the negation of the conjunction operation, expressed in ordinary language as "not both". It is also called non-conjunction, or alternative denial since it says in effect that at least one of its operands is false, or NAND ("not and"). In digital electronics, it corresponds to the NAND gate. It is named after Henry Maurice Sheffer and written as [math]\displaystyle{ \mid }[/math] or as [math]\displaystyle{ \uparrow }[/math] or as [math]\displaystyle{ \overline{\wedge} }[/math] or as [math]\displaystyle{ Dpq }[/math] in Polish notation by Łukasiewicz (but not as ||, often used to represent disjunction).

Its dual is the NOR operator (also known as the Peirce arrow, Quine dagger or Webb operator). Like its dual, NAND can be used by itself, without any other logical operator, to constitute a logical formal system (making NAND functionally complete). This property makes the NAND gate crucial to modern digital electronics, including its use in computer processor design.

Definition

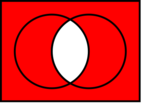
The non-conjunction is a logical operation on two logical values. It produces a value of true, if — and only if — at least one of the propositions is false.

Truth table

The truth table of [math]\displaystyle{ P \uparrow Q }[/math] is as follows.

[math]\displaystyle{ P }[/math] [math]\displaystyle{ Q }[/math] [math]\displaystyle{ P \uparrow Q }[/math]
True True False
True False True
False True True
False False True

Logical equivalences

The Sheffer stroke of [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math] is the negation of their conjunction

[math]\displaystyle{ P \uparrow Q }[/math]   [math]\displaystyle{ \Leftrightarrow }[/math]   [math]\displaystyle{ \neg (P \land Q) }[/math]
Venn1110.svg   [math]\displaystyle{ \Leftrightarrow }[/math]   [math]\displaystyle{ \neg }[/math] Venn0001.svg

By De Morgan's laws, this is also equivalent to the disjunction of the negations of [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math]

[math]\displaystyle{ P \uparrow Q }[/math]   [math]\displaystyle{ \Leftrightarrow }[/math]   [math]\displaystyle{ \neg P }[/math] [math]\displaystyle{ \lor }[/math] [math]\displaystyle{ \neg Q }[/math]
Venn1110.svg   [math]\displaystyle{ \Leftrightarrow }[/math]   Venn1010.svg [math]\displaystyle{ \lor }[/math] Venn1100.svg

Alternative notations and names

Peirce was the first to show the functional completeness of non-conjunction (representing this as [math]\displaystyle{ \overline{\curlywedge} }[/math]) but didn't publish his result.[1][2] Peirce's editor added [math]\displaystyle{ \overline{\curlywedge} }[/math]) for non-disjunction[citation needed].[2]

In 1911, Stamm (pl) was the first to publish a proof of the completeness of non-conjunction, representing this with [math]\displaystyle{ \sim }[/math] (the Stamm hook)[3] and non-disjunction in print at the first time and showed their functional completeness.[4]

In 1913, Sheffer described non-disjunction using [math]\displaystyle{ \mid }[/math] and showed its functional completeness. Sheffer also used [math]\displaystyle{ \wedge }[/math] for non-disjunction.[citation needed] Many people, beginning with Nicod in 1917, and followed by Whitehead, Russell and many others, mistakenly thought Sheffer has described non-conjunction using [math]\displaystyle{ \mid }[/math], naming this the Sheffer Stroke.

In 1928, Hilbert and Ackermann described non-conjunction with the operator [math]\displaystyle{ / }[/math].[5][6]

In 1929, Łukasiewicz used [math]\displaystyle{ D }[/math] in [math]\displaystyle{ Dpq }[/math] for non-conjunction in his Polish notation.[7]

An alternative notation for non-conjunction is [math]\displaystyle{ \uparrow }[/math]. It is not clear who first introduced this notation, although the corresponding [math]\displaystyle{ \downarrow }[/math] for non-disjunction was used by Quine in 1940,.[8]

History

The stroke is named after Henry Maurice Sheffer, who in 1913 published a paper in the Transactions of the American Mathematical Society[9] providing an axiomatization of Boolean algebras using the stroke, and proved its equivalence to a standard formulation thereof by Huntington employing the familiar operators of propositional logic (AND, OR, NOT). Because of self-duality of Boolean algebras, Sheffer's axioms are equally valid for either of the NAND or NOR operations in place of the stroke. Sheffer interpreted the stroke as a sign for nondisjunction (NOR) in his paper, mentioning non-conjunction only in a footnote and without a special sign for it. It was Jean Nicod who first used the stroke as a sign for non-conjunction (NAND) in a paper of 1917 and which has since become current practice.[10][11] Russell and Whitehead used the Sheffer stroke in the 1927 second edition of Principia Mathematica and suggested it as a replacement for the "OR" and "NOT" operations of the first edition.

Charles Sanders Peirce (1880) had discovered the functional completeness of NAND or NOR more than 30 years earlier, using the term ampheck (for 'cutting both ways'), but he never published his finding. Two years before Sheffer, Edward Stamm (pl) also described the NAND and NOR operators and showed that the other Boolean operations could be expressed by it.[4]

Properties

NAND does not possess any of the following five properties, each of which is required to be absent from, and the absence of all of which is sufficient for, at least one member of a set of functionally complete operators: truth-preservation, falsity-preservation, linearity, monotonicity, self-duality. (An operator is truth- (or falsity-)preserving if its value is truth (falsity) whenever all of its arguments are truth (falsity).) Therefore {NAND} is a functionally complete set.

This can also be realized as follows: All three elements of the functionally complete set {AND, OR, NOT} can be constructed using only NAND. Thus the set {NAND} must be functionally complete as well.

Other Boolean operations in terms of the Sheffer stroke

Expressed in terms of NAND [math]\displaystyle{ \uparrow }[/math], the usual operators of propositional logic are:

[math]\displaystyle{ \neg P }[/math]     [math]\displaystyle{ \Leftrightarrow }[/math]     [math]\displaystyle{ P }[/math] [math]\displaystyle{ \uparrow }[/math] [math]\displaystyle{ P }[/math]
Venn10.svg     [math]\displaystyle{ \Leftrightarrow }[/math]     Venn01.svg [math]\displaystyle{ \uparrow }[/math] Venn01.svg
   
[math]\displaystyle{ P \rightarrow Q }[/math]     [math]\displaystyle{ \Leftrightarrow }[/math]     [math]\displaystyle{ ~P }[/math] [math]\displaystyle{ \uparrow }[/math] [math]\displaystyle{ (Q \uparrow Q) }[/math]     [math]\displaystyle{ \Leftrightarrow }[/math]     [math]\displaystyle{ ~P }[/math] [math]\displaystyle{ \uparrow }[/math] [math]\displaystyle{ (P \uparrow Q) }[/math]
Venn1011.svg     [math]\displaystyle{ \Leftrightarrow }[/math]     Venn0101.svg [math]\displaystyle{ \uparrow }[/math] Venn1100.svg     [math]\displaystyle{ \Leftrightarrow }[/math]     Venn0101.svg [math]\displaystyle{ \uparrow }[/math] Venn1110.svg
   
[math]\displaystyle{ P \leftrightarrow Q }[/math]     [math]\displaystyle{ \Leftrightarrow }[/math]     [math]\displaystyle{ (P \uparrow Q) }[/math] [math]\displaystyle{ \uparrow }[/math] [math]\displaystyle{ ((P \uparrow P) \uparrow (Q \uparrow Q)) }[/math]
Venn1001.svg     [math]\displaystyle{ \Leftrightarrow }[/math]     Venn1110.svg [math]\displaystyle{ \uparrow }[/math] Venn0111.svg
 
[math]\displaystyle{ P \land Q }[/math]     [math]\displaystyle{ \Leftrightarrow }[/math]     [math]\displaystyle{ (P \uparrow Q) }[/math] [math]\displaystyle{ \uparrow }[/math] [math]\displaystyle{ (P \uparrow Q) }[/math]
Venn0001.svg     [math]\displaystyle{ \Leftrightarrow }[/math]     Venn1110.svg [math]\displaystyle{ \uparrow }[/math] Venn1110.svg
   
[math]\displaystyle{ P \lor Q }[/math]     [math]\displaystyle{ \Leftrightarrow }[/math]     [math]\displaystyle{ (P \uparrow P) }[/math] [math]\displaystyle{ \uparrow }[/math] [math]\displaystyle{ (Q \uparrow Q) }[/math]
Venn0111.svg     [math]\displaystyle{ \Leftrightarrow }[/math]     Venn1010.svg [math]\displaystyle{ \uparrow }[/math] Venn1100.svg

Formal system based on the Sheffer stroke

The following is an example of a formal system based entirely on the Sheffer stroke, yet having the functional expressiveness of the propositional logic:

Symbols

pn for natural numbers n:

( | )

The Sheffer stroke commutes but does not associate (e.g., (T | T) | F = T, but T | (T | F) = F). Hence any formal system including the Sheffer stroke as an infix symbol must also include a means of indicating grouping (grouping is automatic if the stroke is used as a prefix, thus: || TTF = T and | T | TF = F). We shall employ '(' and ')' to this effect.

We also write p, q, r, … instead of p0, p1, p2.

Syntax

Construction rule I: For each natural number n, the symbol pn is a well-formed formula (WFF), called an atom.

Construction rule II: If X and Y are WFFs, then (X | Y) is a WFF.

Closure rule: Any formulae which cannot be constructed by means of the first two construction rules are not WFFs.

The letters U, V, W, X, and Y are metavariables standing for WFFs.

A decision procedure for determining whether a formula is well-formed goes as follows: "deconstruct" the formula by applying the construction rules backwards, thereby breaking the formula into smaller subformulae. Then repeat this recursive deconstruction process to each of the subformulae. Eventually the formula should be reduced to its atoms, but if some subformula cannot be so reduced, then the formula is not a WFF.

Calculus

All WFFs of the form

((U | (V | W)) | ((Y | (Y | Y)) | ((X | V) | ((U | X) | (U | X)))))

are axioms. Instances of

[math]\displaystyle{ (U | (V | W)), U \vdash W }[/math]

are inference rules.

Simplification

Since the only connective of this logic is |, the symbol | could be discarded altogether, leaving only the parentheses to group the letters. A pair of parentheses must always enclose a pair of WFFs. Examples of theorems in this simplified notation are

(p(p(q(q((pq)(pq)))))),
(p(p((qq)(pp)))).

The notation can be simplified further, by letting

(U) := (UU)
[math]\displaystyle{ ((U)) \equiv U }[/math]

for any U. This simplification causes the need to change some rules:

  1. More than two letters are allowed within parentheses.
  2. Letters or WFFs within parentheses are allowed to commute.
  3. Repeated letters or WFFs within a same set of parentheses can be eliminated.

The result is a parenthetical version of the Peirce existential graphs.

Another way to simplify the notation is to eliminate parentheses by using Polish notation (PN). For example, the earlier examples with only parentheses could be rewritten using only strokes as follows

(p(p(q(q((pq)(pq)))))) becomes
| p | p | q | q || pq | pq, and
(p(p((qq)(pp)))) becomes,
| p | p || qq | pp.

This follows the same rules as the parenthesis version, with the opening parenthesis replaced with a Sheffer stroke and the (redundant) closing parenthesis removed.

Or (for some formulas) one could omit both parentheses and strokes and allow the order of the arguments to determine the order of function application so that for example, applying the function from right to left (reverse Polish notation – any other unambiguous convention based on ordering would do)

[math]\displaystyle{ \begin{align} & pqr \equiv (p\mid (q\mid r)), \text{ whereas} \\ & rqp \equiv (r \mid (q\mid p)). \end{align} }[/math]

See also


References

  1. ↑ Peirce, C. S. (1933). "A Boolian Algebra with One Constant". in Hartshorne, C.; Weiss, P.. Collected Papers of Charles Sanders Peirce, Volume IV The Simplest Mathematics. Massachusetts: Harvard University Press. pp. 13–18. 
  2. ↑ 2.0 2.1 Peirce, C. S. (1933). "The Simplest Mathematics". in Hartshorne, C.; Weiss, P.. Collected Papers of Charles Sanders Peirce, Volume IV The Simplest Mathematics. Massachusetts: Harvard University Press. pp. 189–262. 
  3. ↑ Zach, R. (18 February 2023). "Sheffer stroke before Sheffer: Edward Stamm". https://richardzach.org/2023/02/sheffer-stroke-before-sheffer-edward-stamm/. 
  4. ↑ 4.0 4.1 "Beitrag zur Algebra der Logik" (in de). Monatshefte für Mathematik und Physik 22 (1): 137–149. 1911. doi:10.1007/BF01742795. 
  5. ↑ Hilbert, D.; Ackermann, W. (1928) (in German). Grundzügen der theoretischen Logik (1 ed.). Berlin: Verlag von Julius Springer. p. 9. 
  6. ↑ Hilbert, D.; Ackermann, W. (1950). Luce, R. E.. ed. Principles of Mathematical Logic. New York: Chelsea Publishing Company. p. 11. 
  7. ↑ Łukasiewicz, J. (1958) (in Polish). Elementy logiki matematycznej (2 ed.). Warszawa: Państwowe Wydawnictwo Naukowe. 
  8. ↑ Quine, W. V (1981). Mathematical Logic (Revised ed.). Cambridge, London, New York, New Rochelle, Melbourne and Sydney: Harvard University Press. p. 45. 
  9. ↑ "A set of five independent postulates for Boolean algebras, with application to logical constants". Transactions of the American Mathematical Society 14 (4): 481–488. 1913. doi:10.2307/1988701. 
  10. ↑ "A Reduction in the Number of Primitive Propositions of Logic". Proceedings of the Cambridge Philosophical Society 19: 32–41. 1917. 
  11. ↑ Introduction to mathematical logic. 1. Princeton University Press. 1956. p. 134. 

Further reading

  • Precis of Mathematical Logic (revised ed.). Dordrecht, South Holland, Netherlands: D. Reidel. 1960.  (NB. Edited and translated from the French and German editions: Précis de logique mathématique)
  • "A Boolian Algebra with One Constant". Collected Papers of Charles Sanders Peirce. 4. Cambridge: Harvard University Press. 1931–1935. pp. 12–20. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Sheffer_stroke&oldid=3381768"