Davenport chained rotations

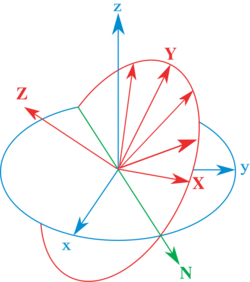
In physics and engineering, Davenport chained rotations are three chained intrinsic rotations about body-fixed specific axes. Euler rotations and Tait–Bryan rotations are particular cases of the Davenport general rotation decomposition. The angles of rotation are called Davenport angles because the general problem of decomposing a rotation in a sequence of three was studied first by Paul B. Davenport. The non-orthogonal rotating coordinate system may be imagined to be rigidly attached to a rigid body. In this case, it is sometimes called a local coordinate system. Given that rotation axes are solidary with the moving body, the generalized rotations can be divided into two groups (here x, y and z refer to the non-orthogonal moving frame):

Generalized Euler rotations

(z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)

Generalized Tait–Bryan rotations

(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z).

Most of the cases belong to the second group, given that the generalized Euler rotations are a degenerated case in which first and third axes are overlapping.

Davenport rotation theorem

Image 1: Davenport possible axes for steps 1 and 3 given Z as the step 2

The general problem of decomposing a rotation into three composed movements about intrinsic axes was studied by P. Davenport, under the name "generalized Euler angles", but later these angles were named "Davenport angles" by M. Shuster and L. Markley.

The general problem consists of obtaining the matrix decomposition of a rotation given the three known axes. In some cases one of the axes is repeated. This problem is equivalent to a decomposition problem of matrices.

Davenport proved that any orientation can be achieved by composing three elemental rotations using non-orthogonal axes. The elemental rotations can either occur about the axes of the fixed coordinate system (extrinsic rotations) or about the axes of a rotating coordinate system, which is initially aligned with the fixed one and modifies its orientation after each elemental rotation (intrinsic rotations).

According to the Davenport theorem, a unique decomposition is possible if and only if the second axis is perpendicular to the other two axes. Therefore, axes 1 and 3 must be in the plane orthogonal to axis 2.

Therefore, decompositions in Euler chained rotations and Tait–Bryan chained rotations are particular cases of this. The Tait–Bryan case appears when axes 1 and 3 are perpendicular, and the Euler case appears when they are overlapping.

Complete system of rotations

Image 2: Airplane resting on a plane

A set of Davenport rotations is said to be complete if it is enough to generate any rotation of the space by composition. Speaking in matrix terms, it is complete if it can generate any orthonormal matrix of the space, whose determinant is +1. Due to the non-commutativity of the matrix product, the rotation system must be ordered.

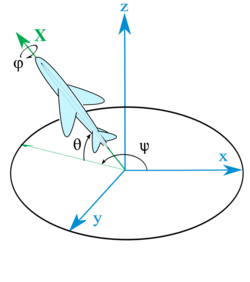
Sometimes the order is imposed by the geometry of the underlying problem. For example, when used for vehicles, which have a special axis pointing to the "forward" direction, only one of the six possible combinations of rotations is useful. The interesting composition is the one able to control the heading and the elevation of the aircraft with one independent rotation each.

In the adjacent drawing, the yaw, pitch and roll (YPR) composition allows adjustment of the direction of an aircraft with the two first angles. A different composition like YRP would allow establishing the direction of the wings axis, which is obviously not useful in most cases.

Tait–Bryan chained rotations

Image 3: The principal axes of an aircraft

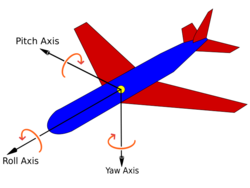
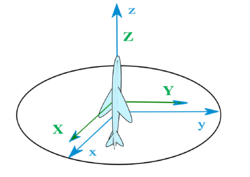
Tait–Bryan rotations are a special case in which the first and third axes are perpendicular among them. Assuming a reference frame ⟨x, y, z⟩ with a convention as in image 2, and a plane with ⟨yaw, pitch, roll⟩ axes like in the image 3Template:Data missing, lying horizontal on the plane ⟨x, y⟩ in the beginning, after performing intrinsic rotations Y, P and R in the yaw, pitch and roll axes (in this order) we obtain something similar to image 4Template:Data missing.

Image 4: Heading, elevation and bank angles after yaw, pitch and roll rotations (Z-Y’-X’’)

In the beginning :

• the plane roll axis is on axis x of the reference frame
• the plane pitch axis is on axis y of the reference frame
• the plane yaw axis is on axis z of the reference frame

The rotations are applied in order yaw, pitch and roll. In these conditions, the Heading (angle on the horizontal plane) will be equal to the yaw applied, and the Elevation will be equal to the pitch.

Matrix expressions for the three Tait–Bryan rotations in 3 dimensions are:

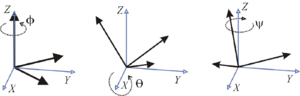
[math]\displaystyle{ \begin{align} \\ R_x(\phi) = \mathrm{Roll}(\phi) &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\phi & -\sin\phi \\ 0 & \sin\phi & \cos\phi \end{bmatrix} \\ R_y(\theta) = \mathrm{Pitch}(\theta) &= \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix} \\ R_z(\psi) = \mathrm{Yaw}(\psi) &= \begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix}. \end{align} }[/math]

The matrix of the composed rotations is

[math]\displaystyle{ \begin{align} M &= \mathrm{Roll}(\phi) \,\mathrm{Pitch}(\theta) \, \mathrm{Yaw}(\psi) \\ &= R_x(\phi) R_z(\psi) R_y(\theta) . \end{align} }[/math]

Of the six possible combinations of yaw, pitch and roll, this combination is the only one in which the heading (direction of the roll axis) is equal to one of the rotations (the yaw), and the elevation (angle of the roll axis with the horizontal plane) is equal to other of the rotations (to the pitch).

Euler chained rotations

Image 5:Starting position of an aircraft to apply proper Euler angles

Euler rotations appear as the special case in which the first and third axes of rotations are overlapping. These Euler rotations are related to the proper Euler angles, which were thought to study the movement of a rigid body such as a planet. The angle to define the direction of the roll axis is normally named "longitude of the revolution axis" or "longitude of the line of nodes" instead of "heading", which makes no sense for a planet.

Anyway, Euler rotations can still be used when speaking about a vehicle, though they will have a weird behavior. As the vertical axis is the origin for the angles, it is named "inclination" instead of "elevation". As before, describing the attitude of a vehicle, there is an axis considered pointing forward, and therefore only one out of the possible combinations of rotations will be useful.

The combination depends on how the axis are taken and what the initial position of the plane is. Using the one in the drawing, and combining rotations in such a way that an axis is repeated, only roll–pitch–roll will allow controlling the longitude and the inclination with one rotation each.

The three matrices to multiply are:

[math]\displaystyle{ \begin{align} R_z(\phi) = \mathrm{Roll}_1(\phi) &= \begin{bmatrix} \cos\phi & -\sin\phi & 0 \\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ R_y(\theta) = \mathrm{Pitch}(\theta) &= \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix} \\ R_z(\psi) = \mathrm{Roll}_2(\psi) &= \begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix}. \end{align} }[/math]

In this convention Roll₁ imposes the "heading", Pitch is the "inclination" (complementary of the elevation), and Roll₂ imposes the "tilt".

Conversion to extrinsic rotations

Image 6: A rotation represented by Euler angles (α, β, γ) = (−60°, 30°, 45°), using z-x’-z″ intrinsic rotations

Image 7: The same rotation represented by (γ, β, α) = (45°, 30°, −60°), using z-x-z extrinsic rotations

Davenport rotations are usually studied as an intrinsic rotation composition, because of the importance of the axes fixed to a moving body, but they can be converted to an extrinsic rotation composition, in case it could be more intuitive.

Any extrinsic rotation is equivalent to an intrinsic rotation by the same angles but with inverted order of elemental rotations, and vice versa. For instance, the intrinsic rotations x-y’-z″ by angles α, β, γ are equivalent to the extrinsic rotations z-y-x by angles γ, β, α. Both are represented by a matrix

[math]\displaystyle{ R = X(\alpha) Y(\beta) Z(\gamma) }[/math]

Where [math]\displaystyle{ X(\alpha) }[/math], [math]\displaystyle{ Y(\beta) }[/math], and [math]\displaystyle{ Z(\gamma) }[/math] are the elementary rotation matrices of the corresponding angles. The product of these matrices, [math]\displaystyle{ R }[/math], should then be pre-multiplied against a column vector. Take note of the ambiguities in the definition of rotation matrices, since some definitions may use row vectors instead.

Relationship with physical motions

Intrinsic rotations

Intrinsic rotations are elemental rotations that occur about the axes of the rotating coordinate system XYZ, which changes its orientation after each elemental rotation. The XYZ system rotates, while xyz is fixed. Starting with XYZ overlapping xyz, a composition of three intrinsic rotations can be used to reach any target orientation for XYZ. The Euler or Tait-Bryan angles (α, β, γ) are the amplitudes of these elemental rotations. For instance, the target orientation can be reached as follows:

• The XYZ system rotates by α about the Z axis (which coincides with the z axis). The X axis now lies on the line of nodes.
• The XYZ system rotates about the now rotated X axis by β. The Z axis is now in its final orientation, and the X axis remains on the line of nodes.
• The XYZ system rotates a third time about the new Z axis by γ.

The above-mentioned notation allows us to summarize this as follows: the three elemental rotations of the XYZ-system occur about z, x’ and z″. Indeed, this sequence is often denoted z-x’-z″. Sets of rotation axes associated with both proper Euler angles and Tait-Bryan angles are commonly named using this notation (see above for details). Sometimes, the same sequence is simply called z-x-z, Z-X-Z, or 3-1-3, but this notation may be ambiguous as it may be identical to that used for extrinsic rotations. In this case, it becomes necessary to separately specify whether the rotations are intrinsic or extrinsic.

Rotation matrices can be used to represent a sequence of intrinsic rotations. For instance,

[math]\displaystyle{ R = X(\alpha) Y(\beta) Z(\gamma) }[/math]

represents a composition of intrinsic rotations about axes x-y’-z″, if used to pre-multiply column vectors. This is standard practice, but take note of the ambiguities in the definition of rotation matrices.

Extrinsic rotations

Extrinsic rotations are elemental rotations that occur about the axes of the fixed coordinate system xyz. The XYZ system rotates, while xyz is fixed. Starting with XYZ overlapping xyz, a composition of three extrinsic rotations can be used to reach any target orientation for XYZ. The Euler or Tait-Bryan angles (α, β, γ) are the amplitudes of these elemental rotations. For instance, the target orientation can be reached as follows:

• The XYZ system rotates about the z axis by α. The X axis is now at angle α with respect to the x axis.
• The XYZ system rotates again about the x axis by β. The Z axis is now at angle β with respect to the z axis.
• The XYZ system rotates a third time about the z axis by γ.

In sum, the three elemental rotations occur about z, x and z. Indeed, this sequence is often denoted z-x-z (or 3-1-3). Sets of rotation axes associated with both proper Euler angles and Tait–Bryan angles are commonly named using this notation (see above for details).

Rotation matrices can be used to represent a sequence of extrinsic rotations. For instance,

[math]\displaystyle{ R = Z(\gamma) Y(\beta) X(\alpha) }[/math]

represents a composition of extrinsic rotations about axes x-y-z, if used to pre-multiply column vectors. This is standard practice, but take note of the ambiguities in the definition of rotation matrices.

Conversion between intrinsic and extrinsic rotations

Image 8: A rotation represented by Euler angles (α, β, γ) = (−60°, 30°, 45°), using z-x’-z″ intrinsic rotations

Image 9: The same rotation represented by (γ, β, α) = (45°, 30°, −60°), using z-x-z extrinsic rotations

Any extrinsic rotation is equivalent to an intrinsic rotation by the same angles but with inverted order of elemental rotations, and vice versa. For instance, the intrinsic rotations x-y’-z″ by angles α, β, γ are equivalent to the extrinsic rotations z-y-x by angles γ, β, α. Both are represented by a matrix

[math]\displaystyle{ R = X(\alpha) Y(\beta) Z(\gamma) }[/math]

if [math]\displaystyle{ R }[/math] is used to pre-multiply column vectors. This is standard practice, but take note of the ambiguities in the definition of rotation matrices.

The proof of the conversion in the pre-multiply case

The rotation matrix of the intrinsic rotation sequence x-y’-z″ can be obtained by the sequential intrinsic element rotations from the right to the left:

[math]\displaystyle{ R = Z''Y'X. }[/math]

In this process there are three frames related in the intrinsic rotation sequence. Let's denote the frame 0 as the initial frame, the frame 1 after the first rotation around the x axis, the frame 2 after the second rotation around the y’ axis, and the frame 3 as the third rotation around z″ axis.

Since a rotation matrix can be represented among these three frames, let's use the left shoulder index to denote the representation frame. The following notation means the rotation matrix that transforms the frame a to the frame b and that is represented in the frame c :

[math]\displaystyle{ {}^c\!R_{a \rightarrow b}. }[/math]

An intrinsic element rotation matrix represented in that frame where the rotation happens has the same value as that of the corresponding extrinsic element rotation matrix:

[math]\displaystyle{ {}^0\!R_{1\rightarrow0} = X, \quad {}^1\!R_{2\rightarrow1} = Y, \quad {}^2\!R_{3\rightarrow2} = Z. }[/math]

The intrinsic element rotation matrix Y’ and Z″ represented in the frame 0 can be expressed as other forms:

[math]\displaystyle{ \begin{align} Y' &= {}^0\!R_{2\rightarrow1} \\ &= {}^0\!R_{1\rightarrow0}{}^1\!R_{2\rightarrow1}{}^0\!R_{1\rightarrow0}^{-1} \\ &= XYX^{-1} \\[3pt] Z'' &= {}^0\!R_{3\rightarrow2} \\ &= {}^0\!R_{1\rightarrow0}{}^1\!R_{3\rightarrow2}{}^0\!R_{1\rightarrow0}^{-1} \\ &= X\left({}^1\!R_{2\rightarrow1}{}^2\!R_{3\rightarrow2}{}^1\!R_{2\rightarrow1}^{-1}\right)X^{-1} \\ &= XYZY^{-1}X^{-1} \end{align} }[/math]

The two equations above are substituted to the first equation:

[math]\displaystyle{ \begin{align} R &= Z''Y'X \\ &= \left(XYZY^{-1}X^{-1}\right)\left(XYX^{-1}\right)X \\ &= XYZY^{-1}\left(X^{-1}X\right)Y\left(X^{-1}X\right) \\ &= XYZ\left(Y^{-1}Y\right) \\ &= XYZ \end{align} }[/math]

Therefore, the rotation matrix of an intrinsic element rotation sequence is the same as that of the inverse extrinsic element rotation sequence:

[math]\displaystyle{ R = Z''Y'X = XYZ. }[/math]

See also

• Matrix decomposition
• Givens rotation