Depth of field

From HandWiki
Short description: Distance between the nearest and the furthest objects that are in focus in an image
A macro photograph showing the defocused effect of a shallow depth of field on a tilted page of text
This photo was taken with an aperture of f/22, creating a mostly in-focus background.
The same scene as above with an aperture of f/1.8. Notice how much blurrier the background appears in this photo.

The depth of field (DOF) is the distance between the nearest and the furthest objects that are in acceptably sharp focus in an image captured with a camera.

Factors affecting depth of field

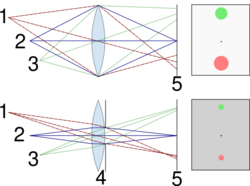
Effect of aperture on blur and DOF (Depth of Field). The points in focus (2) project points onto the image plane (5), but points at different distances (1 and 3) project blurred images, or circles of confusion. Decreasing the aperture size (4) reduces the size of the blur spots for points not in the focused plane, so that the blurring is imperceptible, and all points are within the DOF.

For cameras that can only focus on one object distance at a time, depth of field is the distance between the nearest and the farthest objects that are in acceptably sharp focus in the image.[1] "Acceptably sharp focus" is defined using a property called the "circle of confusion".

The depth of field can be determined by focal length, distance to subject (object to be imaged), the acceptable circle of confusion size, and aperture.[2] Limitations of depth of field can sometimes be overcome with various techniques and equipment. The approximate depth of field can be given by:

[math]\displaystyle{ \text{DOF} \approx \frac{2u^2Nc}{f^2} }[/math]

for a given maximum acceptable circle of confusion (c), focal length (f), f-number (N), and distance to subject (u).[3][4]

As distance or the size of the acceptable circle of confusion increases, the depth of field increases; however, increasing the size of the aperture (i.e., reducing f-number) or increasing the focal length reduces the depth of field. Depth of field changes linearly with f-number and circle of confusion, but changes in proportion to the square of the distance to the subject and inversely in proportion to the square of the focal length. As a result, photos taken at extremely close range (i.e., so small u) have a proportionally much smaller depth of field.

Rearranging the DOF equation shows that it is the ratio between distance and focal length that affects DOF;

[math]\displaystyle{ \text{DOF} \approx 2Nc\left(\frac{u}{f}\right)^2=2Nc\left(1 - \frac{1}{M_T}\right)^2 }[/math]

Note that [math]\displaystyle{ M_T = -\frac{f}{u - f} }[/math] is the transverse magnification which is the ratio of the lateral image size to the lateral subject size.[5]

Image sensor size affects DOF in counterintuitive ways. Because the circle of confusion is directly tied to the sensor size, decreasing the size of the sensor while holding focal length and aperture constant will decrease the depth of field (by the crop factor). The resulting image however will have a different field of view. If the focal length is altered to maintain the field of view, the change in focal length will counter the decrease of DOF from the smaller sensor and increase the depth of field (also by the crop factor).[6][7][8][9]

Effect of lens aperture

For a given subject framing and camera position, the DOF is controlled by the lens aperture diameter, which is usually specified as the f-number (the ratio of lens focal length to aperture diameter). Reducing the aperture diameter (increasing the f-number) increases the DOF because only the light travelling at shallower angles passes through the aperture so only cones of rays with shallower angles reach the image plane. In other words, the circles of confusion are reduced or increasing the DOF.[10]

For a given size of the subject's image in the focal plane, the same f-number on any focal length lens will give the same depth of field.[11] This is evident from the above DOF equation by noting that the ratio u/f is constant for constant image size. For example, if the focal length is doubled, the subject distance is also doubled to keep the subject image size the same. This observation contrasts with the common notion that "focal length is twice as important to defocus as f/stop",[12] which applies to a constant subject distance, as opposed to constant image size.

Motion pictures make limited use of aperture control; to produce a consistent image quality from shot to shot, cinematographers usually choose a single aperture setting for interiors (e.g., scenes inside a building) and another for exteriors (e.g., scenes in an area outside a building), and adjust exposure through the use of camera filters or light levels. Aperture settings are adjusted more frequently in still photography, where variations in depth of field are used to produce a variety of special effects.

Aperture = f/1.4. DOF=0.8 cm
Aperture = f/4.0. DOF=2.2 cm
Aperture = f/22. DOF=12.4 cm
Depth of field for different values of aperture using 50 mm objective lens and full-frame DSLR camera. Focus point is on the first blocks column.[13]

Effect of circle of confusion

Precise focus is only possible at an exact distance from a lens;[lower-alpha 1] at that distance, a point object will produce a small spot image. Otherwise, a point object will produce a larger or blur spot image that is typically and approximately a circle. When this circular spot is sufficiently small, it is visually indistinguishable from a point, and appears to be in focus. The diameter of the largest circle that is indistinguishable from a point is known as the acceptable circle of confusion, or informally, simply as the circle of confusion.

The acceptable circle of confusion depends on how the final image will be used. The circle of confusion as 0.25 mm for an image viewed from 25 cm away is generally accepted.[14]

For 35 mm motion pictures, the image area on the film is roughly 22 mm by 16 mm. The limit of tolerable error was traditionally set at 0.05 mm (0.0020 in) diameter, while for 16 mm film, where the size is about half as large, the tolerance is stricter, 0.025 mm (0.00098 in).[15] More modern practice for 35 mm productions set the circle of confusion limit at 0.025 mm (0.00098 in).[16]

Camera movements

The term "camera movements" refers to swivel (swing and tilt, in modern terminology) and shift adjustments of the lens holder and the film holder. These features have been in use since the 1800s and are still in use today on view cameras, technical cameras, cameras with tilt/shift or perspective control lenses, etc. Swiveling the lens or sensor causes the plane of focus (POF) to swivel, and also causes the field of acceptable focus to swivel with the POF; and depending on the DOF criteria, to also change the shape of the field of acceptable focus. While calculations for DOF of cameras with swivel set to zero have been discussed, formulated, and documented since before the 1940s, documenting calculations for cameras with non-zero swivel seem to have begun in 1990.

More so than in the case of the zero swivel camera, there are various methods to form criteria and set up calculations for DOF when swivel is non-zero. There is a gradual reduction of clarity in objects as they move away from the POF, and at some virtual flat or curved surface the reduced clarity becomes unacceptable. Some photographers do calculations or use tables, some use markings on their equipment, some judge by previewing the image.

When the POF is rotated, the near and far limits of DOF may be thought of as wedge-shaped, with the apex of the wedge nearest the camera; or they may be thought of as parallel to the POF.[17][18]

Object-field calculation methods

Traditional depth-of-field formulas can be hard to use in practice. As an alternative, the same effective calculation can be done without regard to the focal length and f-number.[lower-alpha 2] Moritz von Rohr and later Merklinger observe that the effective absolute aperture diameter can be used for similar formula in certain circumstances.[19]

Moreover, traditional depth-of-field formulas assume equal acceptable circles of confusion for near and far objects. Merklinger[lower-alpha 3] suggested that distant objects often need to be much sharper to be clearly recognizable, whereas closer objects, being larger on the film, do not need to be so sharp.[19] The loss of detail in distant objects may be particularly noticeable with extreme enlargements. Achieving this additional sharpness in distant objects usually requires focusing beyond the hyperfocal distance, sometimes almost at infinity. For example, if photographing a cityscape with a traffic bollard in the foreground, this approach, termed the object field method by Merklinger, would recommend focusing very close to infinity, and stopping down to make the bollard sharp enough. With this approach, foreground objects cannot always be made perfectly sharp, but the loss of sharpness in near objects may be acceptable if recognizability of distant objects is paramount.

Other authors such as Ansel Adams have taken the opposite position, maintaining that slight unsharpness in foreground objects is usually more disturbing than slight unsharpness in distant parts of a scene.[20]

Overcoming DOF limitations

Some methods and equipment allow altering the apparent DOF, and some even allow the DOF to be determined after the image is made. These are based or supported by computational imaging processes. For example, focus stacking combines multiple images focused on different planes, resulting in an image with a greater (or less, if so desired) apparent depth of field than any of the individual source images. Similarly, in order to reconstruct the 3-dimensional shape of an object, a depth map can be generated from multiple photographs with different depths of field. Xiong and Shafer concluded, in part, "...the improvements on precisions of focus ranging and defocus ranging can lead to efficient shape recovery methods."[21]

Another approach is focus sweep. The focal plane is swept across the entire relevant range during a single exposure. This creates a blurred image, but with a convolution kernel that is nearly independent of object depth, so that the blur is almost entirely removed after computational deconvolution. This has the added benefit of dramatically reducing motion blur.[22]

Other technologies use a combination of lens design and post-processing: Wavefront coding is a method by which controlled aberrations are added to the optical system so that the focus and depth of field can be improved later in the process.[23]

The lens design can be changed even more: in colour apodization the lens is modified such that each colour channel has a different lens aperture. For example, the red channel may be f/2.4, green may be f/2.4, whilst the blue channel may be f/5.6. Therefore, the blue channel will have a greater depth of field than the other colours. The image processing identifies blurred regions in the red and green channels and in these regions copies the sharper edge data from the blue channel. The result is an image that combines the best features from the different f-numbers.[24]

At the extreme, a plenoptic camera captures 4D light field information about a scene, so the focus and depth of field can be altered after the photo is taken.

Diffraction and DOF

Diffraction causes images to lose sharpness at high F-numbers (i.e., narrow aperture stop opening sizes), and hence limits the potential depth of field.[25] (This effect is not considered in the above formula giving approximate DOF values.) In general photography this is rarely an issue; because large f-numbers typically require long exposure times to acquire acceptable image brightness, motion blur may cause greater loss of sharpness than the loss from diffraction. However, diffraction is a greater issue in close-up photography, and the overall image sharpness can be degraded as photographers are trying to maximize depth of field with very small apertures.[26][27]

Hansma and Peterson have discussed determining the combined effects of defocus and diffraction using a root-square combination of the individual blur spots.[28][29] Hansma's approach determines the f-number that will give the maximum possible sharpness; Peterson's approach determines the minimum f-number that will give the desired sharpness in the final image and yields a maximum depth of field for which the desired sharpness can be achieved.[lower-alpha 4] In combination, the two methods can be regarded as giving a maximum and minimum f-number for a given situation, with the photographer free to choose any value within the range, as conditions (e.g., potential motion blur) permit. Gibson gives a similar discussion, additionally considering blurring effects of camera lens aberrations, enlarging lens diffraction and aberrations, the negative emulsion, and the printing paper.[25][lower-alpha 5] Couzin gave a formula essentially the same as Hansma's for optimal f-number, but did not discuss its derivation.[30]

Hopkins,[31] Stokseth,[32] and Williams and Becklund[33] have discussed the combined effects using the modulation transfer function.[34][35]

DOF scales

Detail from a lens set to f/11. The point half-way between the 1 m and 2 m marks, the DOF limits at f/11, represents the focus distance of approximately 1.33 m (the reciprocal of the mean of the reciprocals of 1 and 2 being 4/3).
DOF scale on Tessina focusing dial

Many lenses include scales that indicate the DOF for a given focus distance and f-number; the 35 mm lens in the image is typical. That lens includes distance scales in feet and meters; when a marked distance is set opposite the large white index mark, the focus is set to that distance. The DOF scale below the distance scales includes markings on either side of the index that correspond to f-numbers. When the lens is set to a given f-number, the DOF extends between the distances that align with the f-number markings.

Photographers can use the lens scales to work backwards from the desired depth of field to find the necessary focus distance and aperture.[36] For the 35 mm lens shown, if it were desired for the DOF to extend from 1 m to 2 m, focus would be set so that index mark was centered between the marks for those distances, and the aperture would be set to f/11.[lower-alpha 6]

On a view camera, the focus and f-number can be obtained by measuring the depth of field and performing simple calculations. Some view cameras include DOF calculators that indicate focus and f-number without the need for any calculations by the photographer.[37][38]

Hyperfocal distance

Zeiss Ikon Contessa with red marks for hyperfocal distance 20 ft at f/8
This section is an excerpt from Hyperfocal distance[ edit ]
Minox LX camera with hyperfocal red dot

In optics and photography, hyperfocal distance is a distance from a lens beyond which all objects can be brought into an "acceptable" focus. As the hyperfocal distance is the focus distance giving the maximum depth of field, it is the most desirable distance to set the focus of a fixed-focus camera.[39] The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable.

The hyperfocal distance has a property called "consecutive depths of field", where a lens focused at an object whose distance from the lens is at the hyperfocal distance H will hold a depth of field from H/2 to infinity, if the lens is focused to H/2, the depth of field will be from H/3 to H; if the lens is then focused to H/3, the depth of field will be from H/4 to H/2, etc.

Thomas Sutton and George Dawson first wrote about hyperfocal distance (or "focal range") in 1867.[40] Louis Derr in 1906 may have been the first to derive a formula for hyperfocal distance. Rudolf Kingslake wrote in 1951 about the two methods of measuring hyperfocal distance.

Some cameras have their hyperfocal distance marked on the focus dial. For example, on the Minox LX focusing dial there is a red dot between 2 m and infinity; when the lens is set at the red dot, that is, focused at the hyperfocal distance, the depth of field stretches from 2 m to infinity. Some lenses have markings indicating the hyperfocal range for specific f-stops.

Near:far distribution

The DOF beyond the subject is always greater than the DOF in front of the subject. When the subject is at the hyperfocal distance or beyond, the far DOF is infinite, so the ratio is 1:∞; as the subject distance decreases, near:far DOF ratio increases, approaching unity at high magnification. For large apertures at typical portrait distances, the ratio is still close to 1:1.

DOF formulae

This section covers some additional formula for evaluating depth of field; however they are all subject to significant simplifying assumptions: for example, they assume the paraxial approximation of Gaussian optics. They are suitable for practical photography, lens designers would use significantly more complex ones.

Focus and f-number from DOF limits

For given near and far DOF limits [math]\displaystyle{ D_{\mathrm N} }[/math] and [math]\displaystyle{ D_{\mathrm F} }[/math], the required f-number is smallest when focus is set to

[math]\displaystyle{ s = \frac{2 D_{\mathrm N} D_{\mathrm F}}{D_{\mathrm N} + D_{\mathrm F}}, }[/math]

the harmonic mean of the near and far distances. In practice, this is equivalent to the arithmetic mean for shallow depths of field.[41] Sometimes, view camera users refer to the difference [math]\displaystyle{ v_{\mathrm N} - v_{\mathrm F} }[/math] as the focus spread.[42]

Foreground and background blur

If a subject is at distance [math]\displaystyle{ s }[/math] and the foreground or background is at distance [math]\displaystyle{ D }[/math], let the distance between the subject and the foreground or background be indicated by

[math]\displaystyle{ x_{\mathrm d} = |D - s|. }[/math]

The blur disk diameter [math]\displaystyle{ b }[/math] of a detail at distance [math]\displaystyle{ x_\mathrm{d} }[/math] from the subject can be expressed as a function of the subject magnification [math]\displaystyle{ m_\mathrm{s} }[/math], focal length [math]\displaystyle{ f }[/math], f-number [math]\displaystyle{ N }[/math], or alternatively the aperture [math]\displaystyle{ d }[/math], according to

[math]\displaystyle{ b = \frac{fm_\mathrm s}{N} \frac{x_\mathrm{d}}{s \pm x_\mathrm{d}} = dm_\mathrm{s} \frac{x_\mathrm{d}}{D}. }[/math]

The minus sign applies to a foreground object, and the plus sign applies to a background object.

The blur increases with the distance from the subject; when [math]\displaystyle{ b }[/math] is less than the circle of confusion, the detail is within the depth of field.

See also

Notes

  1. ↑ strictly, at an exact distance from a plane
  2. ↑ notwithstanding that the f-number is derived from the focal length
  3. ↑ Englander describes a similar approach in his paper Apparent Depth of Field: Practical Use in Landscape Photography; Conrad discusses this approach, under Different Circles of Confusion for Near and Far Limits of Depth of Field, and The Object Field Method, in Depth of Field in Depth
  4. ↑ Peterson does not give a closed-form expression for the minimum f-number, though such an expression obtains from simple algebraic manipulation of his Equation 3
  5. ↑ The analytical section at the end of Gibson (1975) was originally published as "Magnification and Depth of Detail in Photomacrography" in the Journal of the Photographic Society of America, Vol. 26, No. 6, June 1960
  6. ↑ The focus distance to have the DOF extend between given near and far object distances is the harmonic mean of the object conjugates. Most helicoid-focused lenses are marked with image plane-to-subject distances,[citation needed] so the focus determined from the lens distance scale is not exactly the harmonic mean of the marked near and far distances.

References

Citations

  1. ↑ Salvaggio & Stroebel 2009, pp. 110-.
  2. ↑ Barbara London; Jim Stone; John Upton (2005). Photography (8th ed.). Pearson. pp. 58. ISBN 978-0-13-448202-6. 
  3. ↑ Elizabeth Allen; Sophie Triantaphillidou (2011). The Manual of Photography. Taylor & Francis. pp. 111–. ISBN 978-0-240-52037-7. https://books.google.com/books?id=IfWivY3mIgAC&pg=PA111. 
  4. ↑ "Depth of field". https://graphics.stanford.edu/courses/cs178/applets/dof.html. 
  5. ↑ Hecht, Eugene (2017). "5.2.3 Thin Lenses". Optics (5th ed.). Pearson. pp. 172. ISBN 978-1-292-09693-3. 
  6. ↑ Nasse, H.H. (March 2010). "Depth of Field and Bokeh (Zeiss Whitepaper)". https://lenspire.zeiss.com/photo/app/uploads/2018/04/Article-Bokeh-2010-EN.pdf. 
  7. ↑ "Digital Camera Sensor Sizes: How it Influences Your Photography". https://www.cambridgeincolour.com/tutorials/digital-camera-sensor-size.htm. 
  8. ↑ "Sensor Size, Perspective and Depth of Field". 5 May 2015. https://photographylife.com/sensor-size-perspective-and-depth-of-field. 
  9. ↑ Vinson, Jason (22 January 2016). "The Smaller the Sensor Size, the Shallower Your Depth of Field" (in en). https://fstoppers.com/education/smaller-sensor-size-shallower-your-depth-field-110547. 
  10. ↑ "Why Does a Small Aperture Increase Depth of Field?". 18 May 2012. http://physicssoup.wordpress.com/2012/05/18/why-does-a-small-aperture-increase-depth-of-field/. 
  11. ↑ "DOF2, January 13, 2009 by Michael Reichmann, Luminous Landscape". 13 January 2009. https://luminous-landscape.com/dof2//. 
  12. ↑ "Ken Rockwell". https://www.kenrockwell.com/sony/lenses/50mm-f12.htm. 
  13. ↑ "photoskop: Interactive Photography Lessons". April 25, 2015. http://www.photoskop.com/player.html?l=all&ch=3&sec=0. 
  14. ↑ Savazzi 2011, p. 109.
  15. ↑ Film and Its Techniques. University of California Press. 1966. p. 56. https://books.google.com/books?id=Ocfs3ZsLresC&q=35+mm+motion+picture+film+circle+of+confusion&pg=PA56. Retrieved 24 February 2016. 
  16. ↑ Thomas Ohanian and Natalie Phillips (2013). Digital Filmmaking: The Changing Art and Craft of Making Motion Pictures. CRC Press. p. 96. ISBN 9781136053542. https://books.google.com/books?id=usMqBgAAQBAJ&q=35+mm+motion+picture+film+circle+of+confusion&pg=PA96. Retrieved 24 February 2016. 
  17. ↑ Merklinger 1993, pp. 49–56.
  18. ↑ Tillmanns 1997, p. 71.
  19. ↑ 19.0 19.1 Merklinger 1992.
  20. ↑ Adams 1980, p. 51.
  21. ↑ Xiong, Yalin, and Steven A. Shafer. "Depth from focusing and defocusing." Computer Vision and Pattern Recognition, 1993. Proceedings CVPR'93., 1993 IEEE Computer Society Conference on. IEEE, 1993.
  22. ↑ Bando et al. "Near-Invariant Blur for Depth and 2D Motion via Time-Varying Light Field Analysis." ACM Transactions on Graphics, Vol. 32, No. 2, Article 13, 2013.
  23. ↑ Mary, D.; Roche, M.; Theys, C.; Aime, C. (2013). "Introduction to Wavefront Coding for Incoherent Imaging". EAS Publications Series 59: 77–92. doi:10.1051/eas/1359005. ISSN 1633-4760. Bibcode: 2013EAS....59...77R. https://www.edp-open.org/images/stories/books/fulldl/eas_59/eas59_pp077-092.pdf. 
  24. ↑ Kay 2011.
  25. ↑ 25.0 25.1 Gibson 1975, p. 64.
  26. ↑ Gibson 1975, p. 53.
  27. ↑ Lefkowitz 1979, p. 84.
  28. ↑ Hansma 1996.
  29. ↑ Peterson 1996.
  30. ↑ Couzin 1982.
  31. ↑ Hopkins 1955.
  32. ↑ Stokseth 1969.
  33. ↑ Williams & Becklund 1989.
  34. ↑ "Depth of Field in Depth", Jeff Conrad
  35. ↑ "Photographic Lenses Tutorial", David M. Jacobson, 26 October 1996
  36. ↑ Ray 1994, p. 315.
  37. ↑ Tillmanns 1997, p. 67-68.
  38. ↑ Ray 1994, p. 230-231.
  39. ↑ Kingslake, Rudolf (1951). Lenses in Photography: The Practical Guide to Optics for Photographers. Garden City, NY: Garden City Press. 
  40. ↑ Sutton, Thomas; Dawson, George (1867). A Dictionary of Photography. London: Sampson Low, Son & Marston. https://archive.org/details/dictionaryofphot00sutt. 
  41. ↑ Conrad, Jeff. "Depth of Field in Depth". https://www.largeformatphotography.info/articles/DoFinDepth.pdf. 
  42. ↑ Hansma 1996, p. 55.

Sources

  • Salvaggio, Nanette; Stroebel, Leslie (2009). Basic Photographic Materials and Processes. Taylor & Francis. pp. 110–. ISBN 978-0-240-80984-7. https://books.google.com/books?id=71uE_OrGw5oC&pg=PA110. 
  • Adams, Ansel (1980) (in en). The Camera. New York Graphic Society. ISBN 9780821210925. https://archive.org/details/cameraadam00adam. "Adams, Ansel. 1980. The Camera." 
  • Couzin, Dennis (November 1982). "Depths of Field". SMPTE Journal: 1096–1098. doi:10.5594/J00204.  Available in PDF online.
  • Gibson, H. Lou. 1975. Close-Up Photography and Photomacrography. 2nd combined ed. Kodak Publication No. N-16. Rochester, NY: Eastman Kodak Company, Vol II: Photomacrography. ISBN:0-87985-160-0
  • Hansma, Paul K. 1996. View Camera Focusing in Practice. Photo Techniques, March/April 1996, 54–57. Available as GIF images on the Large Format page.
  • Hopkins, H.H. (1955). "The frequency response of a defocused optical system". Proceedings of the Royal Society A 231 (1184): 91–103. doi:10.1098/rspa.1955.0158. Bibcode: 1955RSPSA.231...91H. 
  • Lefkowitz, Lester. 1979 The Manual of Close-Up Photography. Garden City, NY: Amphoto. ISBN:0-8174-2456-3
  • Merklinger, Harold M. 1992. The INs and OUTs of FOCUS: An Alternative Way to Estimate Depth-of-Field and Sharpness in the Photographic Image. v. 1.0.3. Bedford, Nova Scotia: Seaboard Printing Limited. ISBN:0-9695025-0-8. Version 1.03e available in PDF at http://www.trenholm.org/hmmerk/.
  • Merklinger, Harold M. 1993. Focusing the View Camera: A Scientific Way to Focus the View Camera and Estimate Depth of Field. v. 1.0. Bedford, Nova Scotia: Seaboard Printing Limited. ISBN:0-9695025-2-4. Version 1.6.1 available in PDF at http://www.trenholm.org/hmmerk/.
  • Peterson, Stephen (March–April 1996). "Image Sharpness and Focusing the View Camera". Photo Techniques: 51–53.  Available as GIF images on the Large Format page.
  • Ray, Sidney F. 1994. Photographic Lenses and Optics. Oxford: Focal Press. ISBN:0-240-51387-8
  • Ray, Sidney F. 2000. The geometry of image formation. In The Manual of Photography: Photographic and Digital Imaging, 9th ed. Ed. Ralph E. Jacobson, Sidney F. Ray, Geoffrey G. Atteridge, and Norman R. Axford. Oxford: Focal Press. ISBN:0-240-51574-9
  • Ray, Sidney F. 2002. Applied Photographic Optics. 3rd ed. Oxford: Focal Press. ISBN:0-240-51540-4
  • Shipman, Carl. 1977. SLR Photographers Handbook. Tucson: H.P. Books. ISBN:0-912656-59-X
  • Stokseth, Per A. (October 1969). "Properties of a Defocused Optical System". Journal of the Optical Society of America 59 (10): 1314–1321. doi:10.1364/JOSA.59.001314. 
  • Stroebel, Leslie. 1976. View Camera Technique. 3rd ed. London: Focal Press. ISBN:0-240-50901-3
  • Tillmanns, Urs. 1997. Creative Large Format: Basics and Applications. 2nd ed. Feuerthalen, Switzerland: Sinar AG. ISBN:3-7231-0030-9
  • von Rohr, Moritz. 1906. Die optischen Instrumente. Leipzig: B. G. Teubner
  • Williams, Charles S.; Becklund, Orville (1989). Introduction to the Optical Transfer Function. New York: Wiley. pp. 293–300.  Reprinted 2002, Bellingham, WA: SPIE Press, ISBN:0-8194-4336-0.
  • Williams, John B. 1990. Image Clarity: High-Resolution Photography. Boston: Focal Press. ISBN:0-240-80033-8
  • Andrew Kay, Jonathan Mather, and Harry Walton, "Extended depth of field by colored apodization", Optics Letters, Vol. 36, Issue 23, pp. 4614–4616 (2011).
  • Savazzi, Enrico (2011). Digital Photography for Science (Hardcover). Lulu.com. ISBN 978-0-557-91133-2. https://books.google.com/books?id=YabFAQAAQBAJ&pg=PA109. [self-published source?]

Further reading

  • Hummel, Rob (editor). 2001. American Cinematographer Manual. 8th ed. Hollywood: ASC Press. ISBN:0-935578-15-3

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Depth_of_field&oldid=3382374"