Digital image processing
Digital image processing is the use of a digital computer to process digital images through an algorithm.[1][2] As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing. It allows a much wider range of algorithms to be applied to the input data and can avoid problems such as the build-up of noise and distortion during processing. Since images are defined over two dimensions (perhaps more), digital image processing may be modeled in the form of multidimensional systems. The generation and development of digital image processing are mainly affected by three factors: first, the development of computers;[3] second, the development of mathematics (especially the creation and improvement of discrete mathematics theory);[4] and third, the demand for a wide range of applications in environment, agriculture, military, industry and medical science has increased.[5]
History
Many of the techniques of digital image processing, or digital picture processing as it often was called, were developed in the 1960s, at Bell Laboratories, the Jet Propulsion Laboratory, Massachusetts Institute of Technology, University of Maryland, and a few other research facilities, with application to satellite imagery, wire-photo standards conversion, medical imaging, videophone, character recognition, and photograph enhancement.[6] The purpose of early image processing was to improve the quality of the image. It was aimed for human beings to improve the visual effect of people. In image processing, the input is a low-quality image, and the output is an image with improved quality. Common image processing include image enhancement, restoration, encoding, and compression. The first successful application was the American Jet Propulsion Laboratory (JPL). They used image processing techniques such as geometric correction, gradation transformation, noise removal, etc. on the thousands of lunar photos sent back by the Space Detector Ranger 7 in 1964, taking into account the position of the Sun and the environment of the Moon. The impact of the successful mapping of the Moon's surface map by the computer has been a success. Later, more complex image processing was performed on the nearly 100,000 photos sent back by the spacecraft, so that the topographic map, color map and panoramic mosaic of the Moon were obtained, which achieved extraordinary results and laid a solid foundation for human landing on the Moon.[7]
The cost of processing was fairly high, however, with the computing equipment of that era. That changed in the 1970s, when digital image processing proliferated as cheaper computers and dedicated hardware became available. This led to images being processed in real-time, for some dedicated problems such as television standards conversion. As general-purpose computers became faster, they started to take over the role of dedicated hardware for all but the most specialized and computer-intensive operations. With the fast computers and signal processors available in the 2000s, digital image processing has become the most common form of image processing, and is generally used because it is not only the most versatile method, but also the cheapest.
Image sensors
The basis for modern image sensors is metal–oxide–semiconductor (MOS) technology,[8] invented at Bell Labs between 1955 and 1960,[9][10][11][12][13][14] This led to the development of digital semiconductor image sensors, including the charge-coupled device (CCD) and later the CMOS sensor.[8]
The charge-coupled device was invented by Willard S. Boyle and George E. Smith at Bell Labs in 1969.[15] While researching MOS technology, they realized that an electric charge was the analogy of the magnetic bubble and that it could be stored on a tiny MOS capacitor. As it was fairly straightforward to fabricate a series of MOS capacitors in a row, they connected a suitable voltage to them so that the charge could be stepped along from one to the next.[8] The CCD is a semiconductor circuit that was later used in the first digital video cameras for television broadcasting.[16]
The NMOS active-pixel sensor (APS) was invented by Olympus in Japan during the mid-1980s. This was enabled by advances in MOS semiconductor device fabrication, with MOSFET scaling reaching smaller micron and then sub-micron levels.[17][18] The NMOS APS was fabricated by Tsutomu Nakamura's team at Olympus in 1985.[19] The CMOS active-pixel sensor (CMOS sensor) was later developed by Eric Fossum's team at the NASA Jet Propulsion Laboratory in 1993.[20] By 2007, sales of CMOS sensors had surpassed CCD sensors.[21]
MOS image sensors are widely used in optical mouse technology. The first optical mouse, invented by Richard F. Lyon at Xerox in 1980, used a 5 μm NMOS integrated circuit sensor chip.[22][23] Since the first commercial optical mouse, the IntelliMouse introduced in 1999, most optical mouse devices use CMOS sensors.[24][25]
Image compression
An important development in digital image compression technology was the discrete cosine transform (DCT), a lossy compression technique first proposed by Nasir Ahmed in 1972.[26] DCT compression became the basis for JPEG, which was introduced by the Joint Photographic Experts Group in 1992.[27] JPEG compresses images down to much smaller file sizes, and has become the most widely used image file format on the Internet.[28] Its highly efficient DCT compression algorithm was largely responsible for the wide proliferation of digital images and digital photos,[29] with several billion JPEG images produced every day as of 2015[update].[30]
Medical imaging techniques produce very large amounts of data, especially from CT, MRI and PET modalities. As a result, storage and communications of electronic image data are prohibitive without the use of compression.[31][32] JPEG 2000 image compression is used by the DICOM standard for storage and transmission of medical images. The cost and feasibility of accessing large image data sets over low or various bandwidths are further addressed by use of another DICOM standard, called JPIP, to enable efficient streaming of the JPEG 2000 compressed image data.[33]
Digital signal processor (DSP)
Electronic signal processing was revolutionized by the wide adoption of MOS technology in the 1970s.[34] MOS integrated circuit technology was the basis for the first single-chip microprocessors and microcontrollers in the early 1970s,[35] and then the first single-chip digital signal processor (DSP) chips in the late 1970s.[36][37] DSP chips have since been widely used in digital image processing.[36]
The discrete cosine transform (DCT) image compression algorithm has been widely implemented in DSP chips, with many companies developing DSP chips based on DCT technology. DCTs are widely used for encoding, decoding, video coding, audio coding, multiplexing, control signals, signaling, analog-to-digital conversion, formatting luminance and color differences, and color formats such as YUV444 and YUV411. DCTs are also used for encoding operations such as motion estimation, motion compensation, inter-frame prediction, quantization, perceptual weighting, entropy encoding, variable encoding, and motion vectors, and decoding operations such as the inverse operation between different color formats (YIQ, YUV and RGB) for display purposes. DCTs are also commonly used for high-definition television (HDTV) encoder/decoder chips.[38]
Tasks
Digital image processing allows the use of much more complex algorithms, and hence, can offer both more sophisticated performance at simple tasks, and the implementation of methods which would be impossible by analogue means.
In particular, digital image processing is a concrete application of, and a practical technology based on:
- Classification
- Feature extraction
- Multi-scale signal analysis
- Pattern recognition
- Projection
Some techniques which are used in digital image processing include:
- Anisotropic diffusion
- Hidden Markov models
- Image editing
- Image restoration
- Independent component analysis
- Linear filtering
- Neural networks
- Partial differential equations
- Pixelation
- Point feature matching
- Principal components analysis
- Self-organizing maps
- Wavelets
Digital image transformations
Filtering
Digital filters are used to blur and sharpen digital images. Filtering can be performed by:
- convolution with specifically designed kernels (filter array) in the spatial domain[39]
- masking specific frequency regions in the frequency (Fourier) domain
The following examples show both methods:[40]
| Filter type | Kernel or mask | Example |
|---|---|---|
| Original Image | File:Affine Transformation Original Checkerboard.jpg | |
| Spatial Lowpass | File:Spatial Mean Filter Checkerboard.png | |
| Spatial Highpass | File:Spatial Laplacian Filter Checkerboard.png | |
| Fourier Representation | Pseudo-code:
image = checkerboard F = Fourier Transform of image Show Image: log(1+Absolute Value(F)) |
File:Fourier Space Checkerboard.png |
| Fourier Lowpass | File:Lowpass Butterworth Checkerboard.png | File:Lowpass FFT Filtered checkerboard.png |
| Fourier Highpass | File:Highpass Butterworth Checkerboard.png | File:Highpass FFT Filtered checkerboard.png |
Image padding in Fourier domain filtering
Images are typically padded before being transformed to the Fourier space, the highpass filtered images below illustrate the consequences of different padding techniques:
| Zero padded | Repeated edge padded |
|---|---|
| File:Highpass FFT Filtered checkerboard.png | File:Highpass FFT Replicate.png |
Notice that the highpass filter shows extra edges when zero padded compared to the repeated edge padding.
Filtering code examples
MATLAB example for spatial domain highpass filtering.
img=checkerboard(20); % generate checkerboard
% ************************** SPATIAL DOMAIN ***************************
klaplace=[0 -1 0; -1 5 -1; 0 -1 0]; % Laplacian filter kernel
X=conv2(img,klaplace); % convolve test img with
% 3x3 Laplacian kernel
figure()
imshow(X,[]) % show Laplacian filtered
title('Laplacian Edge Detection')
Affine transformations
Affine transformations enable basic image transformations including scale, rotate, translate, mirror and shear as is shown in the following examples:[40]
| Transformation Name | Affine Matrix | Example |
|---|---|---|
| Identity | File:Checkerboard identity.svg | |
| Reflection | File:Checkerboard reflection.svg | |
| Scale | File:Checkerboard scale.svg | |
| Rotate | File:Checkerboard rotate.svg where θ = π/6 =30° | |
| Shear | File:Checkerboard shear.svg |
To apply the affine matrix to an image, the image is converted to matrix in which each entry corresponds to the pixel intensity at that location. Then each pixel's location can be represented as a vector indicating the coordinates of that pixel in the image, [x, y], where x and y are the row and column of a pixel in the image matrix. This allows the coordinate to be multiplied by an affine-transformation matrix, which gives the position that the pixel value will be copied to in the output image.
However, to allow transformations that require translation transformations, 3-dimensional homogeneous coordinates are needed. The third dimension is usually set to a non-zero constant, usually 1, so that the new coordinate is [x, y, 1]. This allows the coordinate vector to be multiplied by a 3×3 matrix, enabling translation shifts. Thus, the third dimension, i.e. the constant 1, allows translation.
Because matrix multiplication is associative, multiple affine transformations can be combined into a single affine transformation by multiplying the matrix of each individual transformation in the order that the transformations are done. This results in a single matrix that, when applied to a point vector, gives the same result as all the individual transformations performed on the vector [x, y, 1] in sequence. Thus a sequence of affine transformation matrices can be reduced to a single affine transformation matrix.
For example, 2-dimensional coordinates only permit rotation about the origin (0, 0). But 3-dimensional homogeneous coordinates can be used to first translate any point to (0, 0), then perform the rotation, and lastly translate the origin (0, 0) back to the original point (the opposite of the first translation). These three affine transformations can be combined into a single matrix—thus allowing rotation around any point in the image.[41]
Image denoising with mathematical morphology
Mathematical morphology (MM) is a nonlinear image processing framework that analyzes shapes within images by probing local pixel neighborhoods using a small, predefined function called a structuring element. In the context of grayscale images, MM is especially useful for denoising through dilation and erosion—primitive operators that can be combined to build more complex filters.
Suppose we have:
- A discrete grayscale image:
- A structuring element:
Here, defines the neighborhood of relative coordinates over which local operations are computed. The values of bias the image during dilation and erosion.
- Dilation
- Grayscale dilation is defined as:
- For example, the dilation at position (1, 1) is calculated as:
- Erosion
- Grayscale erosion is defined as:
- For example, the erosion at position (1, 1) is calculated as:
Results
After applying dilation to :
After applying erosion to :
Opening and Closing
MM operations, such as opening and closing, are composite processes that utilize both dilation and erosion to modify the structure of an image. These operations are particularly useful for tasks such as noise removal, shape smoothing, and object separation.
- Opening: This operation is performed by applying erosion to an image first, followed by dilation. The purpose of opening is to remove small objects or noise from the foreground while preserving the overall structure of larger objects. It is especially effective in situations where noise appears as isolated bright pixels or small, disconnected features.
For example, applying opening to an image with a structuring element would first reduce small details (through erosion) and then restore the main shapes (through dilation). This ensures that unwanted noise is removed without significantly altering the size or shape of larger objects.
- Closing: This operation is performed by applying dilation first, followed by erosion. Closing is typically used to fill small holes or gaps within objects and to connect broken parts of the foreground. It works by initially expanding the boundaries of objects (through dilation) and then refining the boundaries (through erosion).
For instance, applying closing to the same image would fill in small gaps within objects, such as connecting breaks in thin lines or closing small holes, while ensuring that the surrounding areas are not significantly affected.
Both opening and closing can be visualized as ways of refining the structure of an image: opening simplifies and removes small, unnecessary details, while closing consolidates and connects objects to form more cohesive structures.
| Structuring element | Mask | Code | Example |
|---|---|---|---|
| Original Image | None | Use Matlab to read Original image
original = imread('scene.jpg');
image = rgb2gray(original);
[r, c, channel] = size(image);
se = logical([1 1 1 ; 1 1 1 ; 1 1 1]);
[p, q] = size(se);
halfH = floor(p/2);
halfW = floor(q/2);
time = 3; % denoising 3 times with all method
|
 |
| Dilation | Use Matlab to dilation
imwrite(image, "scene_dil.jpg")
extractmax = zeros(size(image), class(image));
for i = 1 : time
dil_image = imread('scene_dil.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH + 1) : (r - halfH)
dpointD = row - halfH;
dpointU = row + halfH;
dpointL = col - halfW;
dpointR = col + halfW;
dneighbor = dil_image(dpointD:dpointU, dpointL:dpointR);
filter = dneighbor(se);
extractmax(row, col) = max(filter);
end
end
imwrite(extractmax, "scene_dil.jpg");
end
|
 | |
| Erosion | Use Matlab to erosion
imwrite(image, 'scene_ero.jpg');
extractmin = zeros(size(image), class(image));
for i = 1: time
ero_image = imread('scene_ero.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH +1): (r -halfH)
pointDown = row-halfH;
pointUp = row+halfH;
pointLeft = col-halfW;
pointRight = col+halfW;
neighbor = ero_image(pointDown:pointUp,pointLeft:pointRight);
filter = neighbor(se);
extractmin(row, col) = min(filter);
end
end
imwrite(extractmin, "scene_ero.jpg");
end
|
 | |
| Opening | Use Matlab to Opening
imwrite(extractmin, "scene_opening.jpg")
extractopen = zeros(size(image), class(image));
for i = 1 : time
dil_image = imread('scene_opening.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH + 1) : (r - halfH)
dpointD = row - halfH;
dpointU = row + halfH;
dpointL = col - halfW;
dpointR = col + halfW;
dneighbor = dil_image(dpointD:dpointU, dpointL:dpointR);
filter = dneighbor(se);
extractopen(row, col) = max(filter);
end
end
imwrite(extractopen, "scene_opening.jpg");
end
|
 | |
| Closing | Use Matlab to Closing
imwrite(extractmax, "scene_closing.jpg")
extractclose = zeros(size(image), class(image));
for i = 1 : time
ero_image = imread('scene_closing.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH + 1) : (r - halfH)
dpointD = row - halfH;
dpointU = row + halfH;
dpointL = col - halfW;
dpointR = col + halfW;
dneighbor = ero_image(dpointD:dpointU, dpointL:dpointR);
filter = dneighbor(se);
extractclose(row, col) = min(filter);
end
end
imwrite(extractclose, "scene_closing.jpg");
end
|
 |
Applications
Digital camera images
Digital cameras generally include specialized digital image processing hardware – either dedicated chips or added circuitry on other chips – to convert the raw data from their image sensor into a color-corrected image in a standard image file format. Additional post processing techniques increase edge sharpness or color saturation to create more naturally looking images.
Film
Westworld (1973) was the first feature film to use the digital image processing to pixellate photography to simulate an android's point of view.[42] Image processing is also vastly used to produce the chroma key effect that replaces the background of actors with natural or artistic scenery.
Face detection
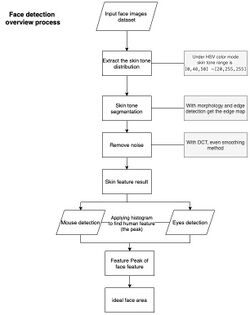
Face detection can be implemented with mathematical morphology, the discrete cosine transform (DCT), and horizontal projection.
General method with feature-based method
The feature-based method of face detection is using skin tone, edge detection, face shape, and feature of a face (like eyes, mouth, etc.) to achieve face detection. The skin tone, face shape, and all the unique elements that only the human face have can be described as features.
Process explanation
- Given a batch of face images, first, extract the skin tone range by sampling face images. The skin tone range is just a skin filter.
- Structural similarity index measure (SSIM) can be applied to compare images in terms of extracting the skin tone.
- Normally, HSV or RGB color spaces are suitable for the skin filter. E.g. HSV mode, the skin tone range is [0,48,50] ~ [20,255,255]
- After filtering images with skin tone, to get the face edge, morphology and DCT are used to remove noise and fill up missing skin areas.
- Opening method or closing method can be used to achieve filling up missing skin.
- DCT is to avoid the object with skin-like tone. Since human faces always have higher texture.
- Sobel operator or other operators can be applied to detect face edge.
- To position human features like eyes, using the projection and find the peak of the histogram of projection help to get the detail feature like mouth, hair, and lip.
- Projection is just projecting the image to see the high frequency which is usually the feature position.
Improvement of image quality method
Image quality can be influenced by camera vibration, over-exposure, gray level distribution too centralized, and noise, etc. For example, noise problem can be solved by smoothing method while gray level distribution problem can be improved by histogram equalization.
Smoothing method
In drawing, if there is some dissatisfied color, taking some color around dissatisfied color and averaging them. This is an easy way to think of Smoothing method.
Smoothing method can be implemented with mask and convolution. Take the small image and mask for instance as below.
image is
mask is
After convolution and smoothing, image is
Observing image[1, 1], image[1, 2], image[2, 1], and image[2, 2].
The original image pixel is 1, 4, 28, 30. After smoothing mask, the pixel becomes 9, 10, 9, 9 respectively.
new image[1, 1] = * (image[0,0]+image[0,1]+image[0,2]+image[1,0]+image[1,1]+image[1,2]+image[2,0]+image[2,1]+image[2,2])
new image[1, 1] = floor( * (2+5+6+3+1+4+1+28+30)) = 9
new image[1, 2] = floor({ * (5+6+5+1+4+6+28+30+2)) = 10
new image[2, 1] = floor( * (3+1+4+1+28+30+7+3+2)) = 9
new image[2, 2] = floor( * (1+4+6+28+30+2+3+2+2)) = 9
Gray Level Histogram method
Generally, given a gray level histogram from an image as below. Changing the histogram to uniform distribution from an image is usually what we called histogram equalization.
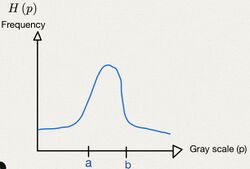
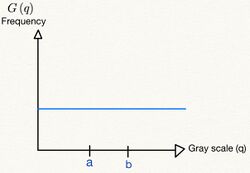
In discrete time, the area of gray level histogram is (see figure 1) while the area of uniform distribution is (see figure 2). It is clear that the area will not change, so .
From the uniform distribution, the probability of is while the
In continuous time, the equation is .
Moreover, based on the definition of a function, the Gray level histogram method is like finding a function that satisfies f(p)=q.
| Improvement method | Issue | Before improvement | Process | After improvement |
|---|---|---|---|---|
| Smoothing method | noise
with Matlab, salt & pepper with 0.01 parameter is added |
 |
|
 |
| Histogram Equalization | Gray level distribution too centralized | 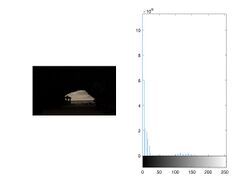 |
Refer to the Histogram equalization | 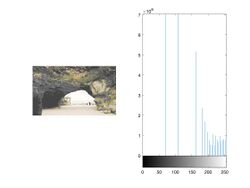 |
Challenges
- Noise and distortions: Imperfections in images due to poor lighting, limited sensors, and file compression can result in unclear images that impact accurate image conversion.
- Variability in image quality: Variations in image quality and resolution, including blurry images and incomplete details, can hinder uniform processing across a database.
- Object detection and Recognition: Identifying and recognising objects within images, especially in complex scenarios with multiple objects and occlusions, poses a significant challenge.
- Data annotation and labelling: Labelling diverse and multiple images for machine recognition is crucial for further processing accuracy, as incorrect identification can lead to unrealistic results.
- Computational resource intensity: Accessing adequate computational resources for image processing can be challenging and costly, hindering progress without sufficient resources.
See also
- Digital imaging
- Computer graphics
- Computer vision
- CVIPtools
- Digitizing
- Fourier transform
- Free boundary condition
- GPGPU
- Homomorphic filtering
- Image analysis
- IEEE Intelligent Transportation Systems Society
- Least-squares spectral analysis
- Medical imaging
- Multidimensional systems
- Relaxation labelling
- Remote sensing software
- Standard test image
- Superresolution
- Total variation denoising
- Machine Vision
- Bounded variation
- Radiomics
- Remote sensing
References
- ↑ Chakravorty, Pragnan (2018). "What is a Signal? [Lecture Notes]". IEEE Signal Processing Magazine 35 (5): 175–177. doi:10.1109/MSP.2018.2832195. Bibcode: 2018ISPM...35e.175C.
- ↑ Gonzalez, Rafael (2018). Digital image processing. New York, NY: Pearson. ISBN 978-0-13-335672-4. OCLC 966609831.
- ↑ Nagornov, Nikolay N.; Lyakhov, Pavel A.; Bergerman, Maxim V.; Kalita, Diana I. (2024). "Modern Trends in Improving the Technical Characteristics of Devices and Systems for Digital Image Processing". IEEE Access 12: 44659–44681. doi:10.1109/ACCESS.2024.3381493. ISSN 2169-3536. Bibcode: 2024IEEEA..1244659N.
- ↑ Yamni, Mohamed; Daoui, Achraf; Abd El-Latif, Ahmed A. (February 2024). "Efficient color image steganography based on new adapted chaotic dynamical system with discrete orthogonal moment transforms" (in en). Mathematics and Computers in Simulation 225: 1170–1198. doi:10.1016/j.matcom.2024.01.023. https://linkinghub.elsevier.com/retrieve/pii/S0378475424000351.
- ↑ Hung, Che-Lun (2020-05-28). "Computational Algorithms on Medical Image Processing" (in en). Current Medical Imaging 16 (5): 467–468. doi:10.2174/157340561605200410144743. PMID 32484080. https://www.eurekaselect.com/180828/article.
- ↑ Azriel Rosenfeld, Picture Processing by Computer, New York: Academic Press, 1969
- ↑ Gonzalez, Rafael C. (2008). Digital image processing. Woods, Richard E. (Richard Eugene), 1954– (3rd ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 23–28. ISBN 978-0-13-168728-8. OCLC 137312858.
- ↑ 8.0 8.1 8.2 Williams, J. B. (2017). The Electronics Revolution: Inventing the Future. Springer. pp. 245–8. ISBN 978-3-319-49088-5. https://books.google.com/books?id=v4QlDwAAQBAJ&pg=PA245.
- ↑ , Derick & Carl J. Frosch"Oxidation of semiconductive surfaces for controlled diffusion" patent US2802760A, issued 1957-08-13
- ↑ Frosch, C. J.; Derick, L (1957). "Surface Protection and Selective Masking during Diffusion in Silicon" (in en). Journal of the Electrochemical Society 104 (9): 547. doi:10.1149/1.2428650. https://iopscience.iop.org/article/10.1149/1.2428650.
- ↑ KAHNG, D. (1961). "Silicon-Silicon Dioxide Surface Device". Technical Memorandum of Bell Laboratories: 583–596. doi:10.1142/9789814503464_0076. ISBN 978-981-02-0209-5. https://doi.org/10.1142/9789814503464_0076.
- ↑ Lojek, Bo (2007). History of Semiconductor Engineering. Berlin, Heidelberg: Springer-Verlag Berlin Heidelberg. p. 321. ISBN 978-3-540-34258-8.
- ↑ Ligenza, J.R.; Spitzer, W.G. (1960). "The mechanisms for silicon oxidation in steam and oxygen" (in en). Journal of Physics and Chemistry of Solids 14: 131–136. doi:10.1016/0022-3697(60)90219-5. Bibcode: 1960JPCS...14..131L. https://linkinghub.elsevier.com/retrieve/pii/0022369760902195.
- ↑ Lojek, Bo (2007). History of Semiconductor Engineering. Springer Science & Business Media. p. 120. ISBN 9783540342588.
- ↑ James R. Janesick (2001). Scientific charge-coupled devices. SPIE Press. pp. 3–4. ISBN 978-0-8194-3698-6. https://books.google.com/books?id=3GyE4SWytn4C&pg=PA3.
- ↑ Boyle, William S; Smith, George E. (1970). "Charge Coupled Semiconductor Devices". Bell Syst. Tech. J. 49 (4): 587–593. doi:10.1002/j.1538-7305.1970.tb01790.x. Bibcode: 1970BSTJ...49..587B.
- ↑ Fossum, Eric R. (12 July 1993). "Active pixel sensors: Are CCDS dinosaurs?". in Blouke, Morley M.. Charge-Coupled Devices and Solid State Optical Sensors III. Proceedings of the SPIE. 1900. pp. 2–14. doi:10.1117/12.148585. Bibcode: 1993SPIE.1900....2F.
- ↑ Fossum, Eric R. (2007). "Active Pixel Sensors". http://ericfossum.com/Publications/Papers/Active%20Pixel%20Sensors%20LASER%20FOCUS.pdf.
- ↑ Matsumoto, Kazuya et al. (1985). "A new MOS phototransistor operating in a non-destructive readout mode". Japanese Journal of Applied Physics 24 (5A): L323. doi:10.1143/JJAP.24.L323. Bibcode: 1985JaJAP..24L.323M.
- ↑ Fossum, Eric R.; Hondongwa, D. B. (2014). "A Review of the Pinned Photodiode for CCD and CMOS Image Sensors". IEEE Journal of the Electron Devices Society 2 (3): 33–43. doi:10.1109/JEDS.2014.2306412.
- ↑ "CMOS Image Sensor Sales Stay on Record-Breaking Pace". IC Insights. 8 May 2018. http://www.icinsights.com/news/bulletins/CMOS-Image-Sensor-Sales-Stay-On-RecordBreaking-Pace/.
- ↑ Lyon, Richard F. (2014). "The Optical Mouse: Early Biomimetic Embedded Vision". Advances in Embedded Computer Vision. Springer. pp. 3–22 (3). ISBN 9783319093871. https://books.google.com/books?id=p_GbBQAAQBAJ&pg=PA3.
- ↑ Lyon, Richard F. (August 1981). "The Optical Mouse, and an Architectural Methodology for Smart Digital Sensors". VLSI Systems and Computations. Computer Science Press. pp. 1–19. doi:10.1007/978-3-642-68402-9_1. ISBN 978-3-642-68404-3. http://bitsavers.trailing-edge.com/pdf/xerox/parc/techReports/VLSI-81-1_The_Optical_Mouse.pdf.
- ↑ Brain, Marshall; Carmack, Carmen (24 April 2000). "How Computer Mice Work" (in en). https://computer.howstuffworks.com/mouse4.htm.
- ↑ Benchoff, Brian (17 April 2016). "Building the First Digital Camera". http://hackaday.com/2016/04/17/building-the-first-digital-camera/. "the Cyclops was the first digital camera"
- ↑ Ahmed, Nasir (January 1991). "How I Came Up With the Discrete Cosine Transform". Digital Signal Processing 1 (1): 4–5. doi:10.1016/1051-2004(91)90086-Z. Bibcode: 1991DSP.....1....4A. https://www.scribd.com/doc/52879771/DCT-History-How-I-Came-Up-with-the-Discrete-Cosine-Transform. Retrieved 10 October 2019.
- ↑ "T.81 – Digital compression and coding of continuous-tone still images – requirements and guidelines". CCITT. September 1992. https://www.w3.org/Graphics/JPEG/itu-t81.pdf.
- ↑ Svetlik, Joe (31 May 2018). "The JPEG image format explained". BT Group. https://home.bt.com/tech-gadgets/photography/what-is-a-jpeg-11364206889349.
- ↑ Caplan, Paul (24 September 2013). "What Is a JPEG? The Invisible Object You See Every Day". https://www.theatlantic.com/technology/archive/2013/09/what-is-a-jpeg-the-invisible-object-you-see-every-day/279954/.
- ↑ Baraniuk, Chris (15 October 2015). "JPeg lockdown: Restriction options sought by committee". BBC News. https://www.bbc.co.uk/news/technology-34538705.
- ↑ Nagornov, Nikolay N.; Lyakhov, Pavel A.; Valueva, Maria V.; Bergerman, Maxim V. (2022). "RNS-Based FPGA Accelerators for High-Quality 3D Medical Image Wavelet Processing Using Scaled Filter Coefficients". IEEE Access 10: 19215–19231. doi:10.1109/ACCESS.2022.3151361. ISSN 2169-3536. Bibcode: 2022IEEEA..1019215N. "Medical imaging systems produce increasingly accurate images with improved quality using higher spatial resolutions and color bit-depth. Such improvements increase the amount of information that needs to be stored, processed, and transmitted.".
- ↑ Dhouib, D.; Naït-Ali, A.; Olivier, C.; Naceur, M.S. (June 2021). "ROI-Based Compression Strategy of 3D MRI Brain Datasets for Wireless Communications" (in en). IRBM 42 (3): 146–153. doi:10.1016/j.irbm.2020.05.001. https://linkinghub.elsevier.com/retrieve/pii/S1959031820300853. "Because of the large amount of medical imaging data, the transmission process becomes complicated in telemedicine applications. Thus, in order to adapt the data bit streams to the constraints related to the limitation of the bandwidths a reduction of the size of the data by compression of the images is essential.".
- ↑ Xin, Gangtao; Fan, Pingyi (2021-06-11). "A lossless compression method for multi-component medical images based on big data mining" (in en). Scientific Reports 11 (1): 12372. doi:10.1038/s41598-021-91920-x. ISSN 2045-2322. PMID 34117350.
- ↑ Grant, Duncan Andrew; Gowar, John (1989). Power MOSFETS: theory and applications. Wiley. p. 1. ISBN 978-0-471-82867-9. https://books.google.com/books?id=ZiZTAAAAMAAJ. "The metal–oxide–semiconductor field-effect transistor (MOSFET) is the most commonly used active device in the very large-scale integration of digital integrated circuits (VLSI). During the 1970s these components revolutionized electronic signal processing, control systems and computers."
- ↑ Shirriff, Ken (30 August 2016). "The Surprising Story of the First Microprocessors". IEEE Spectrum (Institute of Electrical and Electronics Engineers) 53 (9): 48–54. doi:10.1109/MSPEC.2016.7551353. https://spectrum.ieee.org/the-surprising-story-of-the-first-microprocessors. Retrieved 13 October 2019.
- ↑ 36.0 36.1 "1979: Single Chip Digital Signal Processor Introduced". Computer History Museum. https://www.computerhistory.org/siliconengine/single-chip-digital-signal-processor-introduced/.
- ↑ Taranovich, Steve (27 August 2012). "30 years of DSP: From a child's toy to 4G and beyond". https://www.edn.com/design/systems-design/4394792/30-years-of-DSP--From-a-child-s-toy-to-4G-and-beyond.
- ↑ Stanković, Radomir S.; Astola, Jaakko T. (2012). "Reminiscences of the Early Work in DCT: Interview with K.R. Rao". Reprints from the Early Days of Information Sciences 60. http://ticsp.cs.tut.fi/reports/ticsp-report-60-reprint-rao-corrected.pdf. Retrieved 13 October 2019.
- ↑ Zhang, M. Z.; Livingston, A. R.; Asari, V. K. (2008). "A High Performance Architecture for Implementation of 2-D Convolution with Quadrant Symmetric Kernels". International Journal of Computers and Applications 30 (4): 298–308. doi:10.1080/1206212x.2008.11441909.
- ↑ 40.0 40.1 Gonzalez, Rafael (2008). Digital Image Processing, 3rd. Pearson Hall. ISBN 978-0-13-168728-8.
- ↑ House, Keyser (6 December 2016). Affine Transformations. Foundations of Physically Based Modeling & Animation. A K Peters/CRC Press. ISBN 978-1-4822-3460-2. https://people.cs.clemson.edu/~dhouse/courses/401/notes/affines-matrices.pdf. Retrieved 26 March 2019.
- ↑ A Brief, Early History of Computer Graphics in Film , Larry Yaeger, 16 August 2002 (last update), retrieved 24 March 2010
Further reading
- Solomon, C.J.; Breckon, T.P. (2010). Fundamentals of Digital Image Processing: A Practical Approach with Examples in Matlab. Wiley-Blackwell. doi:10.1002/9780470689776. ISBN 978-0-470-84473-1.
- Wilhelm Burger; Mark J. Burge (2007). Digital Image Processing: An Algorithmic Approach Using Java. Springer. ISBN 978-1-84628-379-6. http://www.imagingbook.com/.
- R. Fisher; K Dawson-Howe; A. Fitzgibbon; C. Robertson; E. Trucco (2005). Dictionary of Computer Vision and Image Processing. John Wiley. ISBN 978-0-470-01526-1.
- Rafael C. Gonzalez; Richard E. Woods; Steven L. Eddins (2004). Digital Image Processing using MATLAB. Pearson Education. ISBN 978-81-7758-898-9.
- Tim Morris (2004). Computer Vision and Image Processing. Palgrave Macmillan. ISBN 978-0-333-99451-1.
- Vipin Tyagi (2018). Understanding Digital Image Processing. Taylor and Francis CRC Press. ISBN 978-11-3856-6842.
- Milan Sonka; Vaclav Hlavac; Roger Boyle (1999). Image Processing, Analysis, and Machine Vision. PWS Publishing. ISBN 978-0-534-95393-5.
- Gonzalez, Rafael C.; Woods, Richard E. (2008). Digital image processing. Upper Saddle River, N.J.: Prentice Hall. ISBN 978-0-13-168728-8. OCLC 137312858.
- Kovalevsky, Vladimir (2019). Modern algorithms for image processing: computer imagery by example using C#. [New York, New York]. ISBN 978-1-4842-4237-7. OCLC 1080084533.
External links
- Lectures on Image Processing, by Alan Peters. Vanderbilt University. Updated 7 January 2016.
- Processing digital images with computer algorithms
- Pengertian Citra Digital: Pemahaman Dasar dan Penerapannya dalam Teknologi
Template:Digital image processing
 |
