Discrete tomography

From HandWiki
Short description: Reconstruction of binary images from a small number of their projections
A discrete tomography reconstruction problem for two vertical and horizontal directions (left), together with its (non-unique) solution (right). The task is to color some of the white points black so that the number of black points in the rows and columns match the blue numbers.

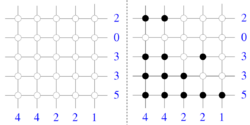
Discrete tomography[1][2] focuses on the problem of reconstruction of binary images (or finite subsets of the integer lattice) from a small number of their projections.

In general, tomography deals with the problem of determining shape and dimensional information of an object from a set of projections. From the mathematical point of view, the object corresponds to a function and the problem posed is to reconstruct this function from its integrals or sums over subsets of its domain. In general, the tomographic inversion problem may be continuous or discrete. In continuous tomography both the domain and the range of the function are continuous and line integrals are used. In discrete tomography the domain of the function may be either discrete or continuous, and the range of the function is a finite set of real, usually nonnegative numbers. In continuous tomography when a large number of projections is available, accurate reconstructions can be made by many different algorithms. It is typical for discrete tomography that only a few projections (line sums) are used. In this case, conventional techniques all fail. A special case of discrete tomography deals with the problem of the reconstruction of a binary image from a small number of projections. The name discrete tomography is due to Larry Shepp, who organized the first meeting devoted to this topic (DIMACS Mini-Symposium on Discrete Tomography, September 19, 1994, Rutgers University).

Theory

Discrete tomography has strong connections with other mathematical fields, such as number theory,[3][4][5] discrete mathematics,[6][7][8] computational complexity theory[9][10] and combinatorics.[11][12][13] In fact, a number of discrete tomography problems were first discussed as combinatorial problems. In 1957, H. J. Ryser found a necessary and sufficient condition for a pair of vectors being the two orthogonal projections of a discrete set. In the proof of his theorem, Ryser also described a reconstruction algorithm, the very first reconstruction algorithm for a general discrete set from two orthogonal projections. In the same year, David Gale found the same consistency conditions, but in connection with the network flow problem.[14] Another result of Ryser's is the definition of the switching operation by which discrete sets having the same projections can be transformed into each other.

The problem of reconstructing a binary image from a small number of projections generally leads to a large number of solutions. It is desirable to limit the class of possible solutions to only those that are typical of the class of the images which contains the image being reconstructed by using a priori information, such as convexity or connectedness.

Theorems

  • Reconstructing (finite) planar lattice sets from their 1-dimensional X-rays is an NP-hard problem if the X-rays are taken from [math]\displaystyle{ m\geq 3 }[/math] lattice directions (for [math]\displaystyle{ m=2 }[/math] the problem is in P).[9]
  • The reconstruction problem is highly unstable for [math]\displaystyle{ m\geq 3 }[/math] (meaning that a small perturbation of the X-rays may lead to completely different reconstructions)[15] and stable for [math]\displaystyle{ m=2 }[/math], see.[15][16][17]
  • Coloring a grid using [math]\displaystyle{ k }[/math] colors with the restriction that each row and each column has a specific number of cells of each color is known as the [math]\displaystyle{ (k-1) }[/math]−atom problem in the discrete tomography community. The problem is NP-hard for [math]\displaystyle{ k \geq 3 }[/math], see.[10]

For further results see.[1][2]

Algorithms

Among the reconstruction methods one can find algebraic reconstruction techniques (e.g., DART[18] [19] or [20]), greedy algorithms (see [21] for approximation guarantees), and Monte Carlo algorithms.[22][23]

Applications

Various algorithms have been applied in image processing ,[18] medicine, three-dimensional statistical data security problems, computer tomograph assisted engineering and design, electron microscopy [24][25] and materials science, including the 3DXRD microscope.[22][23][26]

A form of discrete tomography also forms the basis of nonograms, a type of logic puzzle in which information about the rows and columns of a digital image is used to reconstruct the image.[27]

See also

References

  1. ↑ 1.0 1.1 Herman, G. T. and Kuba, A., Discrete Tomography: Foundations, Algorithms, and Applications, Birkhäuser Boston, 1999
  2. ↑ 2.0 2.1 Herman, G. T. and Kuba, A., Advances in Discrete Tomography and Its Applications, Birkhäuser Boston, 2007
  3. ↑ R.J. Gardner, P. Gritzmann, Discrete tomography: determination of finite sets by X-rays, Trans. Amer. Math. Soc. 349 (1997), no. 6, 2271-2295.
  4. ↑ L. Hajdu, R. Tijdeman, Algebraic aspects of discrete tomography, J. reine angew. Math. 534 (2001), 119-128.
  5. ↑ A. Alpers, R. Tijdeman, The Two-Dimensional Prouhet-Tarry-Escott Problem, Journal of Number Theory, 123 (2), pp. 403-412, 2007 [1].
  6. ↑ S. Brunetti, A. Del Lungo, P. Gritzmann, S. de Vries, On the reconstruction of binary and permutation matrices under (binary) tomographic constraints. Theoret. Comput. Sci. 406 (2008), no. 1-2, 63-71.
  7. ↑ A. Alpers, P. Gritzmann, On Stability, Error Correction, and Noise Compensation in Discrete Tomography, SIAM Journal on Discrete Mathematics 20 (1), pp. 227-239, 2006 [2]
  8. ↑ P. Gritzmann, B. Langfeld, On the index of Siegel grids and its application to the tomography of quasicrystals. European J. Combin. 29 (2008), no. 8, 1894-1909.
  9. ↑ 9.0 9.1 R.J. Gardner, P. Gritzmann, D. Prangenberg, On the computational complexity of reconstructing lattice sets from their X-rays. Discrete Math. 202 (1999), no. 1-3, 45-71.
  10. ↑ 10.0 10.1 C. Dürr, F. Guiñez, M. Matamala, Reconstructing 3-Colored Grids from Horizontal and Vertical Projections Is NP-hard. ESA 2009: 776-787.
  11. ↑ H.J. Ryser, Matrices of zeros and ones, Bull. Amer. Math. Soc. 66 1960 442-464.
  12. ↑ D. Gale, A theorem on flows in networks, Pacific J. Math. 7 (1957), 1073-1082.
  13. ↑ E. Barcucci, S. Brunetti, A. Del Lungo, M. Nivat, Reconstruction of lattice sets from their horizontal, vertical and diagonal X-rays, Discrete Mathematics 241(1-3): 65-78 (2001).
  14. ↑ Brualdi, Richard A. (2006). Combinatorial matrix classes. Encyclopedia of Mathematics and Its Applications. 108. Cambridge: Cambridge University Press. p. 27. ISBN 978-0-521-86565-4. https://archive.org/details/combinatorialmat0000brua/page/27. 
  15. ↑ 15.0 15.1 A. Alpers, P. Gritzmann, L. Thorens, Stability and Instability in Discrete Tomography, Lecture Notes in Computer Science 2243; Digital and Image Geometry (Advanced Lectures), G. Bertrand, A. Imiya, R. Klette (Eds.), pp. 175-186, Springer-Verlag, 2001.
  16. ↑ A. Alpers, S. Brunetti, On the Stability of Reconstructing Lattice Sets from X-rays Along Two Directions, Lecture Notes in Computer Science 3429; Digital Geometry for Computer Imagery, E. Andres, G. Damiand, P. Lienhardt (Eds.), pp. 92-103, Springer-Verlag, 2005.
  17. ↑ B. van Dalen, Stability results for uniquely determined sets from two directions in discrete tomography, Discrete Mathematics 309(12): 3905-3916 (2009).
  18. ↑ 18.0 18.1 Batenburg, Joost; Sijbers, Jan - DART: A practical reconstruction algorithm for discrete tomography - In: IEEE transactions on image processing, Vol. 20, Nr. 9, p. 2542-2553, (2011). doi:10.1109/TIP.2011.2131661
  19. ↑ W. van Aarle, K J. Batenburg, and J. Sijbers, Automatic parameter estimation for the Discrete Algebraic Reconstruction Technique (DART), IEEE Transactions on Image Processing, 2012 [3]
  20. ↑ K. J. Batenburg, and J. Sijbers, "Generic iterative subset algorithms for discrete tomography", Discrete Applied Mathematics, vol. 157, no. 3, pp. 438-451, 2009
  21. ↑ P. Gritzmann, S. de Vries, M. Wiegelmann, Approximating binary images from discrete X-rays, SIAM J. Optim. 11 (2000), no. 2, 522-546.
  22. ↑ 22.0 22.1 A. Alpers, H.F. Poulsen, E. Knudsen, G.T. Herman, A Discrete Tomography Algorithm for Improving the Quality of 3DXRD Grain Maps, Journal of Applied Crystallography 39, pp. 582-588, 2006 [4].
  23. ↑ 23.0 23.1 L. Rodek, H.F. Poulsen, E. Knudsen, G.T. Herman, A stochastic algorithm for reconstruction of grain maps of moderately deformed specimens based on X-ray diffraction, Journal of Applied Crystallography 40:313-321, 2007.
  24. ↑ S. Bals, K. J. Batenburg, J. Verbeeck, J. Sijbers and G. Van Tendeloo, "Quantitative 3D reconstruction of catalyst particles for bamboo-like carbon-nanotubes", Nano Letters, Vol. 7, Nr. 12, p. 3669-3674, (2007) doi:10.1021/nl071899m
  25. ↑ Batenburg J., S. Bals, Sijbers J., C. Kubel, P.A. Midgley, J.C. Hernandez, U. Kaiser, E.R. Encina, E.A. Coronado and G. Van Tendeloo, "3D imaging of nanomaterials by discrete tomography", Ultramicroscopy, Vol. 109, p. 730-740, (2009) doi:10.1016/j.ultramic.2009.01.009
  26. ↑ K. J. Batenburg, J. Sijbers, H. F. Poulsen, and E. Knudsen, "DART: A Robust Algorithm for Fast Reconstruction of 3D Grain Maps", Journal of Applied Crystallography, vol. 43, pp. 1464-1473, 2010
  27. ↑ Games Magazine Presents Paint by Numbers. Random House. 1994. ISBN 978-0-8129-2384-1. https://books.google.com/books?id=K98BAAAACAAJ. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Discrete_tomography&oldid=2639677"