Earth:Consolidation (soil)
Consolidation refers to the process by which soils change volume in response to a change in pressure.[1] According to the "father of soil mechanics", Karl von Terzaghi, consolidation is "any process which involves a decrease in water content of saturated soil without replacement of water by air". In general it is the process in which reduction in volume takes place by expulsion of water under long-term static loads. It occurs when stress is applied to a soil that causes the soil particles to pack together more tightly. When this occurs in a soil that is saturated with water, water will be squeezed out of the soil. The magnitude of consolidation can be predicted by many different methods. In the Classical Method, developed by Terzaghi, soils are tested with an oedometer test to determine their compression index. This can be used to predict the amount of consolidation.
When stress is removed from a consolidated soil, the soil will rebound, regaining some of the volume it had lost in the consolidation process. If the stress is reapplied, the soil will consolidate again along a recompression curve, defined by the recompression index. The soil which had its load removed is considered to be "overconsolidated". This is the case for soils that have previously had glaciers on them. The highest stress that it has been subjected to is termed the "preconsolidation stress". The "over-consolidation ratio" (OCR) is defined as the highest stress experienced divided by the current stress. A soil that is currently experiencing its highest stress is said to be "normally consolidated" and has an OCR of one. A soil could be considered "underconsolidated" immediately after a new load is applied but before the excess pore water pressure has dissipated.
Consolidation analysis
Spring analogy
The process of consolidation is often explained with an idealized system composed of a spring, a container with a hole in its cover, and water. In this system, the spring represents the compressibility or the structure of the soil itself, and the water which fills the container represents the pore water in the soil.
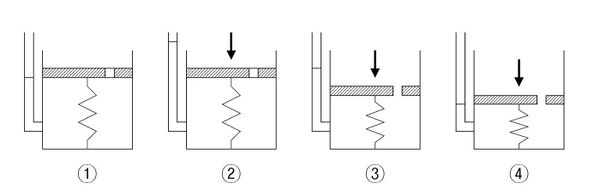
- The container is completely filled with water, and the hole is closed. (Fully saturated soil)
- A load is applied onto the cover, while the hole is still unopened. At this stage, only the water resists the applied load. (Development of excess pore water pressure)
- As soon as the hole is opened, water starts to drain out through the hole and the spring shortens. (Drainage of excess pore water pressure)
- After some time, the drainage of water no longer occurs. Now, the spring alone resists the applied load. (Full dissipation of excess pore water pressure. End of consolidation)
Primary consolidation
This method assumes consolidation occurs in only one-dimension. Laboratory data is used to construct a plot of strain or void ratio versus effective stress where the effective stress axis is on a logarithmic scale. The plot's slope is the compression index or recompression index. The equation for consolidation settlement of a normally consolidated soil can then be determined to be:
[math]\displaystyle{ \delta_c = \frac{ C_c }{ 1 + e_0 } H \log \left( \frac{ \sigma_{zf}' }{ \sigma_{z0}' } \right) \ }[/math]
where
- δc is the settlement due to consolidation.
- Cc is the compression index.
- e0 is the initial void ratio.
- H is the height of the compressible soil.
- σzf is the final vertical stress.
- σz0 is the initial vertical stress.
Cc can be replaced by Cr (the recompression index) for use in overconsolidated soils where the final effective stress is less than the preconsolidation stress. When the final effective stress is greater than the preconsolidation stress, the two equations must be used in combination to model both the recompression portion and the virgin compression portion of the consolidation processes, as follows,
[math]\displaystyle{ \delta_c = \frac{ C_r }{ 1 + e_0 } H \log \left( \frac{ \sigma_{zc}' }{ \sigma_{z0}' } \right) + \frac{ C_c }{ 1 + e_0 } H \log \left( \frac{ \sigma_{zf}' }{ \sigma_{zc}' } \right)\ }[/math]
where σzc is the preconsolidation stress of the soil.
Secondary consolidation
Secondary compression is the compression of soil that takes place after primary consolidation. Even after the reduction of hydrostatic pressure some compression of soil takes place at slow rate. This is known as secondary compression. Secondary compression is caused by creep, viscous behavior of the clay-water system, compression of organic matter, and other processes. In sand, settlement caused by secondary compression is negligible, but in peat, a soil with very high organic content, it is very significant. Due to transfer of stresses to points of contact of soil grains some of the highly viscous water between the points of contact is forced out.
Secondary compression is given by the formula
[math]\displaystyle{ S_s=\frac{H_0}{1+e_0} C_{a} \log \left( \frac {t} {t_{95} } \right) \ }[/math]
Where H0 is the height of the consolidating medium
e0 is the initial void ratio
Ca is the secondary compression index
t is the length of time after consolidation considered
t95 is the length of time for achieving 95% consolidation
Time dependency
The time for consolidation to occur can be predicted. Sometimes consolidation can take years. This is especially true in saturated clays because their hydraulic conductivity is extremely low, and this causes the water to take an exceptionally long time to drain out of the soil. While drainage is occurring, the pore water pressure is greater than normal because it is carrying part of the applied stress (as opposed to the soil particles).
[math]\displaystyle{ T_v=\frac{c_v*t}{(H_{dr})^2} \ }[/math]
Where Tv is the time factor.
Hdr is the average longest drain path during consolidation.
t is the time at measurement
Cv is defined as the coefficient of consolidation found using the log method with
[math]\displaystyle{ C_v=\frac{T_{50}H_{dr}^2}{t_{50}} }[/math]
or the root method with
[math]\displaystyle{ C_v=\frac{T_{95}H_{dr}^2}{t_{95}} }[/math]
t50 time to 50% deformation (consolidation) and t95 is 95%
Where T95=1.129 T50=0.197
See also
- Compaction (geology)
- Soil mechanics
- Vacuum consolidation
References
- ↑ Schofield, Andrew Noel; Wroth, Peter (1968) (in en). Critical State Soil Mechanics. McGraw-Hill. https://books.google.co.uk/books/about/Critical_State_Soil_Mechanics.html?id=Z-YeAQAAIAAJ&redir_esc=y.
Bibliography
- Coduto, Donald (2001), Foundation Design, Prentice-Hall, ISBN 0-13-589706-8
- Kim, Myung-mo (2000) (in ko), Soil Mechanics (4 ed.), Seoul: Munundang, ISBN 89-7393-053-2
- Terzaghi, Karl (1943), Theoretical soil mechanics, John Wiley&Sons, Inc., p. 265
 |
