Physics:Creep (deformation)

Short description: Tendency of a solid material to move slowly or deform permanently under mechanical stress

The movement of ice in a glacier is an example of creeping in solids.

In materials science, creep (sometimes called cold flow) is the tendency of a solid material to undergo slow deformation while subject to persistent mechanical stresses. It can occur as a result of long-term exposure to high levels of stress that are still below the yield strength of the material. Creep is more severe in materials that are subjected to heat for long periods and generally increase as they near their melting point.

The rate of deformation is a function of the material's properties, exposure time, exposure temperature and the applied structural load. Depending on the magnitude of the applied stress and its duration, the deformation may become so large that a component can no longer perform its function – for example creep of a turbine blade could cause the blade to contact the casing, resulting in the failure of the blade. Creep is usually of concern to engineers and metallurgists when evaluating components that operate under high stresses or high temperatures. Creep is a deformation mechanism that may or may not constitute a failure mode. For example, moderate creep in concrete is sometimes welcomed because it relieves tensile stresses that might otherwise lead to cracking.

Unlike brittle fracture, creep deformation does not occur suddenly upon the application of stress. Instead, strain accumulates as a result of long-term stress. Therefore, creep is a "time-dependent" deformation.

Temperature dependence

The temperature range in which creep deformation may occur differs in various materials. Creep deformation generally occurs when a material is stressed at a temperature near its melting point. While tungsten requires a temperature in the thousands of degrees before creep deformation can occur, lead may creep at room temperature, and ice will creep at temperatures below 0 °C (32 °F). Plastics and low-melting-temperature metals, including many solders, can begin to creep at room temperature. Glacier flow is an example of creep processes in ice. The effects of creep deformation generally become noticeable at approximately 35% of the melting point (in Kelvin) for metals and at 45% of melting point for ceramics.

Stages

Strain (ε) as a function of time due to constant stress over an extended period for a Class M material

Creep behavior can be split into three main stages.

In primary, or transient, creep, the strain rate is a function of time. In Class M materials, which include most pure materials, primary strain rate decreases over time. This can be due to increasing dislocation density, or it can be due to evolving grain size. In class A materials, which have large amounts of solid solution hardening, strain rate increases over time due to a thinning of solute drag atoms as dislocations move.

In the secondary, or steady-state, creep, dislocation structure and grain size have reached equilibrium, and therefore strain rate is constant. Equations that yield a strain rate refer to the steady-state strain rate. Stress dependence of this rate depends on the creep mechanism.

In tertiary creep, the strain rate exponentially increases with stress. This can be due to necking phenomena, internal cracks, or voids, which all decrease the cross-sectional area and increase the true stress on the region, further accelerating deformation and leading to fracture.

Mechanisms of deformation

Depending on the temperature and stress, different deformation mechanisms are activated. Though there are generally many deformation mechanisms active at all times, usually one mechanism is dominant, accounting for almost all deformation.

Various mechanisms are:

• Bulk diffusion (Nabarro–Herring creep)
• Grain boundary diffusion (Coble creep)
• Glide-controlled dislocation creep: dislocations move via glide and climb, and the speed of glide is the dominant factor on strain rate
• Climb-controlled dislocation creep: dislocations move via glide and climb, and the speed of climb is the dominant factor on strain rate
• Harper–Dorn creep: a low-stress creep mechanism in some pure materials

At low temperatures and low stress, creep is essentially nonexistent and all strain is elastic. At low temperatures and high stress, materials experience plastic deformation rather than creep. At high temperatures and low stress, diffusional creep tends to be dominant, while at high temperatures and high stress, dislocation creep tends to be dominant.

Deformation mechanism maps

Deformation mechanism maps provide a visual tool categorizing the dominant deformation mechanism as a function of homologous temperature, shear modulus-normalized stress, and strain rate. Generally, two of these three properties (most commonly temperature and stress) are the axes of the map, while the third is drawn as contours on the map.

To populate the map, constitutive equations are found for each deformation mechanism. These are used to solve for the boundaries between each deformation mechanism, as well as the strain rate contours. Deformation mechanism maps can be used to compare different strengthening mechanisms, as well as compare different types of materials.

General equation

[math]\displaystyle{ \frac{\mathrm{d}\varepsilon}{\mathrm{d}t} = \frac{C\sigma^m}{d^b} e^\frac{-Q}{kT} }[/math]

where ε is the creep strain, C is a constant dependent on the material and the particular creep mechanism, m and b are exponents dependent on the creep mechanism, Q is the activation energy of the creep mechanism, σ is the applied stress, d is the grain size of the material, k is Boltzmann's constant, and T is the absolute temperature.

Dislocation creep

At high stresses (relative to the shear modulus), creep is controlled by the movement of dislocations. For dislocation creep, Q = Q(self diffusion), 4 ≤ m ≤ 6, and b < 1. Therefore, dislocation creep has a strong dependence on the applied stress and the intrinsic activation energy and a weaker dependence on grain size. As grain size gets smaller, grain boundary area gets larger, so dislocation motion is impeded.

Some alloys exhibit a very large stress exponent (m > 10), and this has typically been explained by introducing a "threshold stress," σ_th, below which creep can't be measured. The modified power law equation then becomes:

[math]\displaystyle{ \frac{\mathrm{d}\varepsilon}{\mathrm{d}t} = A \left(\sigma-\sigma_{\rm th}\right)^m e^\frac{-Q}{\bar R T} }[/math]

where A, Q and m can all be explained by conventional mechanisms (so 3 ≤ m ≤ 10), and R is the gas constant. The creep increases with increasing applied stress, since the applied stress tends to drive the dislocation past the barrier, and make the dislocation get into a lower energy state after bypassing the obstacle, which means that the dislocation is inclined to pass the obstacle. In other words, part of the work required to overcome the energy barrier of passing an obstacle is provided by the applied stress and the remainder by thermal energy.

Nabarro–Herring creep

A diagram showing the diffusion of atoms and vacancies under Nabarro–Herring creep

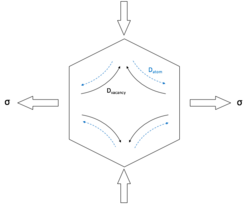
Nabarro–Herring (NH) creep is a form of diffusion creep, while dislocation glide creep does not involve atomic diffusion. Nabarro–Herring creep dominates at high temperatures and low stresses. As shown in the figure on the right, the lateral sides of the crystal are subjected to tensile stress and the horizontal sides to compressive stress. The atomic volume is altered by applied stress: it increases in regions under tension and decreases in regions under compression. So the activation energy for vacancy formation is changed by ±σΩ, where Ω is the atomic volume, the positive value is for compressive regions and negative value is for tensile regions. Since the fractional vacancy concentration is proportional to exp(−Q_f ± σΩ/RT), where Q_f is the vacancy-formation energy, the vacancy concentration is higher in tensile regions than in compressive regions, leading to a net flow of vacancies from the regions under tension to the regions under compression, and this is equivalent to a net atom diffusion in the opposite direction, which causes the creep deformation: the grain elongates in the tensile stress axis and contracts in the compressive stress axis.

In Nabarro–Herring creep, k is related to the diffusion coefficient of atoms through the lattice, Q = Q(self diffusion), m = 1, and b = 2. Therefore, Nabarro–Herring creep has a weak stress dependence and a moderate grain size dependence, with the creep rate decreasing as the grain size is increased.

Nabarro–Herring creep is strongly temperature dependent. For lattice diffusion of atoms to occur in a material, neighboring lattice sites or interstitial sites in the crystal structure must be free. A given atom must also overcome the energy barrier to move from its current site (it lies in an energetically favorable potential well) to the nearby vacant site (another potential well). The general form of the diffusion equation is

[math]\displaystyle{ D = D_0e^{\frac{E}{KT}} }[/math]

where D₀ has a dependence on both the attempted jump frequency and the number of nearest neighbor sites and the probability of the sites being vacant. Thus there is a double dependence upon temperature. At higher temperatures the diffusivity increases due to the direct temperature dependence of the equation, the increase in vacancies through Schottky defect formation, and an increase in the average energy of atoms in the material. Nabarro–Herring creep dominates at very high temperatures relative to a material's melting temperature.

Coble creep

Coble creep is the second form of diffusion controlled creep. In Coble creep the atoms diffuse along grain boundaries to elongate the grains along the stress axis. This causes Coble creep to have a stronger grain size dependence than Nabarro–Herring creep, thus, Coble creep will be more important in materials composed of very fine grains. For Coble creep k is related to the diffusion coefficient of atoms along the grain boundary, Q = Q(grain boundary diffusion), m = 1, and b = 3. Because Q(grain boundary diffusion) is less than Q(self diffusion), Coble creep occurs at lower temperatures than Nabarro–Herring creep. Coble creep is still temperature dependent, as the temperature increases so does the grain boundary diffusion. However, since the number of nearest neighbors is effectively limited along the interface of the grains, and thermal generation of vacancies along the boundaries is less prevalent, the temperature dependence is not as strong as in Nabarro–Herring creep. It also exhibits the same linear dependence on stress as Nabarro–Herring creep. Generally, the diffusional creep rate should be the sum of Nabarro–Herring creep rate and Coble creep rate. Diffusional creep leads to grain-boundary separation, that is, voids or cracks form between the grains. To heal this, grain-boundary sliding occurs. The diffusional creep rate and the grain boundary sliding rate must be balanced if there are no voids or cracks remaining. When grain-boundary sliding can not accommodate the incompatibility, grain-boundary voids are generated, which is related to the initiation of creep fracture.

Solute drag creep

Solute drag creep is one of the mechanisms for power-law creep (PLC), involving both dislocation and diffusional flow. Solute drag creep is observed in certain metallic alloys. In these alloys, the creep rate increases during the first stage of creep (Transient creep) before reaching a steady-state value. This phenomenon can be explained by a model associated with solid-solution strengthening. At low temperatures, the solute atoms are immobile and increase the flow stress required to move dislocations. However, at higher temperatures, the solute atoms are more mobile and may form atmospheres and clouds surrounding the dislocations. This is especially likely if the solute atom has a large misfit in the matrix. The solutes are attracted by the dislocation stress fields and are able to relieve the elastic stress fields of existing dislocations. Thus the solutes become bound to the dislocations. The concentration of solute, C, at a distance, r, from a dislocation is given by the Cottrell atmosphere defined as

[math]\displaystyle{ C_r = C_0 \exp\left(-\frac{\beta\sin\theta}{rKT}\right) }[/math]

where C₀ is the concentration at r = ∞ and β is a constant which defines the extent of segregation of the solute. When surrounded by a solute atmosphere, dislocations that attempt to glide under an applied stress are subjected to a back stress exerted on them by the cloud of solute atoms. If the applied stress is sufficiently high, the dislocation may eventually break away from the atmosphere, allowing the dislocation to continue gliding under the action of the applied stress. The maximum force (per unit length) that the atmosphere of solute atoms can exert on the dislocation is given by Cottrell and Jaswon

[math]\displaystyle{ \frac{F_{\rm max}}{L} = \frac{C_0 \beta^2}{bkT} }[/math]

When the diffusion of solute atoms is activated at higher temperatures, the solute atoms which are "bound" to the dislocations by the misfit can move along with edge dislocations as a "drag" on their motion if the dislocation motion or the creep rate is not too high. The amount of "drag" exerted by the solute atoms on the dislocation is related to the diffusivity of the solute atoms in the metal at that temperature, with a higher diffusivity leading to lower drag and vice versa. The velocity at which the dislocations glide can be approximated by a power law of the form

[math]\displaystyle{ v = B {\sigma^*}^m B =B_0 \exp\left(\frac{-Q_{\rm g}}{RT}\right) }[/math]

where m is the effective stress exponent, Q is the apparent activation energy for glide and B₀ is a constant. The parameter B in the above equation was derived by Cottrell and Jaswon for interaction between solute atoms and dislocations on the basis of the relative atomic size misfit ε_a of solutes to be

[math]\displaystyle{ B= \frac{9kT}{MG^2b^4\ln\frac{r2}{r1}} \cdot \frac{D_{\rm sol}}{\varepsilon_{\rm a}^2c_0} }[/math]

where k is Boltzmann's constant, and r₁ and r₂ are the internal and external cut-off radii of dislocation stress field. c₀ and D_sol are the atomic concentration of the solute and solute diffusivity respectively. D_sol also has a temperature dependence that makes a determining contribution to Q_g.

If the cloud of solutes does not form or the dislocations are able to break away from their clouds, glide occurs in a jerky manner where fixed obstacles, formed by dislocations in combination with solutes, are overcome after a certain waiting time with support by thermal activation. The exponent m is greater than 1 in this case. The equations show that the hardening effect of solutes is strong if the factor B in the power-law equation is low so that the dislocations move slowly and the diffusivity D_sol is low. Also, solute atoms with both high concentration in the matrix and strong interaction with dislocations are strong gardeners. Since misfit strain of solute atoms is one of the ways they interact with dislocations, it follows that solute atoms with large atomic misfit are strong gardeners. A low diffusivity D_sol is an additional condition for strong hardening.

Solute drag creep sometimes shows a special phenomenon, over a limited strain rate, which is called the Portevin–Le Chatelier effect. When the applied stress becomes sufficiently large, the dislocations will break away from the solute atoms since dislocation velocity increases with the stress. After breakaway, the stress decreases and the dislocation velocity also decreases, which allows the solute atoms to approach and reach the previously departed dislocations again, leading to a stress increase. The process repeats itself when the next local stress maximum is obtained. So repetitive local stress maxima and minima could be detected during solute drag creep.

Dislocation climb-glide creep

Dislocation climb-glide creep is observed in materials at high temperature. The initial creep rate is larger than the steady-state creep rate. Climb-glide creep could be illustrated as follows: when the applied stress is not enough for a moving dislocation to overcome the obstacle on its way via dislocation glide alone, the dislocation could climb to a parallel slip plane by diffusional processes, and the dislocation can glide on the new plane. This process repeats itself each time when the dislocation encounters an obstacle. The creep rate could be written as:

[math]\displaystyle{ \frac{\mathrm{d}\varepsilon}{\mathrm{d}t} = \frac{A_{\rm CG}D_{\rm L}}{\sqrt M}\left(\frac{\sigma\Omega}{kT}\right)^{4.5} }[/math]

where A_CG includes details of the dislocation loop geometry, D_L is the lattice diffusivity, M is the number of dislocation sources per unit volume, σ is the applied stress, and Ω is the atomic volume. The exponent m for dislocation climb-glide creep is 4.5 if M is independent of stress and this value of m is consistent with results from considerable experimental studies.

Harper–Dorn creep

Harper–Dorn creep is a climb-controlled dislocation mechanism at low stresses that has been observed in aluminum, lead, and tin systems, in addition to nonmetal systems such as ceramics and ice. It was first observed by Harper and Dorn in 1957. It is characterized by two principal phenomena: a power-law relationship between the steady-state strain rate and applied stress at a constant temperature which is weaker than the natural power-law of creep, and an independent relationship between the steady-state strain rate and grain size for a provided temperature and applied stress. The latter observation implies that Harper–Dorn creep is controlled by dislocation movement; namely, since creep can occur by vacancy diffusion (Nabarro–Herring creep, Coble creep), grain boundary sliding, and/or dislocation movement, and since the first two mechanisms are grain-size dependent, Harper–Dorn creep must therefore be dislocation-motion dependent. The same was also confirmed in 1972 by Barrett and co-workers where FeAl₃ precipitates lowered the creep rates by 2 orders of magnitude compared to highly pure Al, thus, indicating Harper–Dorn creep to be a dislocation based mechanism.

Equation

Harper–Dorn creep is typically overwhelmed by other creep mechanisms in most situations, and is therefore not observed in most systems. The phenomenological equation which describes Harper–Dorn creep is

[math]\displaystyle{ \frac{\mathrm{d}\varepsilon}{\mathrm{d}t} = \rho_0 \frac{D_{\rm v} G b^3}{k T} \left(\frac{\sigma_{\rm s}^n} G \right) }[/math]

where ρ₀ is dislocation density (constant for Harper–Dorn creep), D_v is the diffusivity through the volume of the material, G is the shear modulus and b is the Burgers vector, σ_s, and n is the stress exponent which varies between 1 and 3.

Later investigation of the creep region

Twenty-five years after Harper and Dorn published their work, Mohamed and Ginter made an important contribution in 1982 by evaluating the potential for achieving Harper–Dorn creep in samples of Al using different processing procedures. The experiments showed that Harper–Dorn creep is achieved with stress exponent n = 1, and only when the internal dislocation density prior to testing is exceptionally low. By contrast, Harper–Dorn creep was not observed in polycrystalline Al and single crystal Al when the initial dislocation density was high.

However, various conflicting reports demonstrate the uncertainties at very low stress levels. One report by Blum and Maier, claimed that the experimental evidence for Harper–Dorn creep is not fully convincing. They argued that the necessary condition for Harper–Dorn creep is not fulfilled in Al with 99.99% purity and the steady-state stress exponent n of the creep rate is always much larger than 1.

The subsequent work conducted by Ginter et al. confirmed that Harper–Dorn creep was attained in Al with 99.9995% purity but not in Al with 99.99% purity and, in addition, the creep curves obtained in the very high purity material exhibited regular and periodic accelerations. They also found that the creep behavior no longer follows a stress exponent of n = 1 when the tests are extended to very high strains of >0.1 but instead there is evidence for a stress exponent of n > 2.

Requirements for the occurrence

• Harper–Dorn creep is usually regarded as a Newtonian viscous process with n = 1. Some very recent experimental evidence suggests that the stress exponent may be closer to ~2. Harper–Dorn creep should be observed at a low-stress creep regime where the stress exponent is lower than in the conventional power-law regime where n ≈ 3–5.
• Unlike Nabarro–Herring diffusion depending on grain size, the Harper–Dorn flow process is independent of grain size. In the initial experiments of Harper and Dorn, identical creep rates are recorded either over a wide range of grain sizes in polycrystalline samples or in a combination of polycrystalline samples and single crystals.
• The measured creep rates should be significantly faster, typically by more than two orders of magnitude, than the creep rates anticipated for Nabarro–Herring diffusion creep. At very high testing temperatures, Coble diffusion creep will be of negligible significance under these conditions.
• The volumetric activation energy indicates that the rate of Harper–Dorn creep is controlled by vacancy diffusion to and from dislocations, resulting in climb-controlled dislocation motion. Unlike in other creep mechanisms, the dislocation density here is constant and independent of the applied stress.
• The dislocation density must be low for Harper–Dorn creep to dominate. The density has been proposed to increase as dislocations move via cross-slip from one slip-plane to another, thereby increasing the dislocation length per unit volume. Cross-slip can also result in jogs along the length of the dislocation, which, if large enough, can act as single-ended dislocation sources.

Future expectation

Harper–Dorn creep is considered as a distinct mechanism under some conditions. But more definitive experiments are needed both to more fully establish the precise requirements for observing this process and to provide detailed information used to develop a more appropriate theoretical flow mechanism.

Sintering

At high temperatures, it is energetically favorable for voids to shrink in a material. The application of tensile stress opposes the reduction in energy gained by void shrinkage. Thus, a certain magnitude of applied tensile stress is required to offset these shrinkage effects and cause void growth and creep fracture in materials at high temperature. This stress occurs at the sintering limit of the system.

The stress tending to shrink voids that must be overcome is related to the surface energy and surface area-volume ratio of the voids. For a general void with surface energy γ and principle radii of curvature of r₁ and r₂, the sintering limit stress is

[math]\displaystyle{ \sigma_{\rm sint} = \frac{\gamma}{r_1}+\frac{\gamma}{r_2} }[/math]

Below this critical stress, voids will tend to shrink rather than grow. Additional void shrinkage effects will also result from the application of a compressive stress. For typical descriptions of creep, it is assumed that the applied tensile stress exceeds the sintering limit.

Creep also explains one of several contributions to densification during metal powder sintering by hot pressing. A main aspect of densification is the shape change of the powder particles. Since this change involves permanent deformation of crystalline solids, it can be considered a plastic deformation process and thus sintering can be described as a high temperature creep process. The applied compressive stress during pressing accelerates void shrinkage rates and allows a relation between the steady-state creep power law and densification rate of the material. This phenomenon is observed to be one of the main densification mechanisms in the final stages of sintering, during which the densification rate (assuming gas-free pores) can be explained by:

[math]\displaystyle{ \dot{\rho}=\frac{3A}{2}\frac{\rho(1-\rho)}{\left(1-(1-\rho)^\frac1n\right)^n}\left(\frac32\frac{P_{\rm e}}{n}\right)^n }[/math]

in which ρ̇ is the densification rate, ρ is the density, P_e is the pressure applied, n describes the exponent of strain rate behavior, and A is a mechanism-dependent constant. A and n are from the following form of the general steady-state creep equation,

[math]\displaystyle{ \dot{\varepsilon}=A\sigma^n }[/math]

where ε̇ is the strain rate, and σ is the tensile stress. For the purposes of this mechanism, the constant A comes from the following expression, where A′ is a dimensionless, experimental constant, μ is the shear modulus, b is the Burgers vector, k is Boltzmann's constant, T is absolute temperature, D₀ is the diffusion coefficient, and Q is the diffusion activation energy:

[math]\displaystyle{ A = A'\frac{D_0 \mu b}{kT} \exp\left(-\frac{Q}{kT}\right) }[/math]

Examples

Polymers

a) Applied stress and b) induced strain as functions of time over a short period for a viscoelastic material

Creep can occur in polymers and metals which are considered viscoelastic materials. When a polymeric material is subjected to an abrupt force, the response can be modeled using the Kelvin–Voigt model. In this model, the material is represented by a Hookean spring and a Newtonian dashpot in parallel. The creep strain is given by the following convolution integral:

[math]\displaystyle{ \varepsilon(t) = \sigma C_0 + \sigma C \int_0^\infty f(\tau)\left(1-e^{-t/\tau}\right) \,\mathrm{d} \tau }[/math]

where σ is applied stress, C₀ is instantaneous creep compliance, C is creep compliance coefficient, τ is retardation time, and f(τ) is the distribution of retardation times.

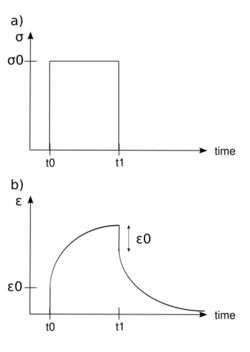
When subjected to a step constant stress, viscoelastic materials experience a time-dependent increase in strain. This phenomenon is known as viscoelastic creep.

At a time t₀, a viscoelastic material is loaded with a constant stress that is maintained for a sufficiently long time period. The material responds to the stress with a strain that increases until the material ultimately fails. When the stress is maintained for a shorter time period, the material undergoes an initial strain until a time t₁ at which the stress is relieved, at which time the strain immediately decreases (discontinuity) then continues decreasing gradually to a residual strain.

Viscoelastic creep data can be presented in one of two ways. Total strain can be plotted as a function of time for a given temperature or temperatures. Below a critical value of applied stress, a material may exhibit linear viscoelasticity. Above this critical stress, the creep rate grows disproportionately faster. The second way of graphically presenting viscoelastic creep in a material is by plotting the creep modulus (constant applied stress divided by total strain at a particular time) as a function of time. Below its critical stress, the viscoelastic creep modulus is independent of the stress applied. A family of curves describing strain versus time response to various applied stress may be represented by a single viscoelastic creep modulus versus time curve if the applied stresses are below the material's critical stress value.

Additionally, the molecular weight of the polymer of interest is known to affect its creep behavior. The effect of increasing molecular weight tends to promote secondary bonding between polymer chains and thus make the polymer more creep resistant. Similarly, aromatic polymers are even more creep resistant due to the added stiffness from the rings. Both molecular weight and aromatic rings add to polymers' thermal stability, increasing the creep resistance of a polymer.

Both polymers and metals can creep. Polymers experience significant creep at temperatures above around −200 °C (−330 °F); however, there are three main differences between polymeric and metallic creep. In metals, creep is not linearly viscoelastic, it is not recoverable, and it is only present at high temperatures.

Polymers show creep basically in two different ways. At typical work loads (5% up to 50%) ultra-high-molecular-weight polyethylene (Spectra, Dyneema) will show time-linear creep, whereas polyester or aramids (Twaron, Kevlar) will show a time-logarithmic creep.

Wood

Wood is considered as an orthotropic material, exhibiting different mechanical properties in three mutually perpendicular directions. Experiments show that the tangential direction in solid wood tend display a slightly higher creep compliance than in the radial direction. In the longitudinal direction, the creep compliance is relatively low and usually do not show any time-dependency in comparison to the other directions.

It has also been shown that there is a substantial difference in viscoelastic properties of wood depending on loading modality (creep in compression or tension). Studies have shown that certain Poisson's ratios gradually go from positive to negative values during the duration of the compression creep test, which does not occur in tension.

Concrete

The creep of concrete, which originates from the calcium silicate hydrates (C-S-H) in the hardened Portland cement paste (which is the binder of mineral aggregates), is fundamentally different from the creep of metals as well as polymers. Unlike the creep of metals, it occurs at all stress levels and, within the service stress range, is linearly dependent on the stress if the pore water content is constant. Unlike the creep of polymers and metals, it exhibits multi-months aging, caused by chemical hardening due to hydration which stiffens the microstructure, and multi-year aging, caused by long-term relaxation of self-equilibrated microstresses in the nanoporous microstructure of the C-S-H. If concrete is fully dried it does not creep, though it is difficult to dry concrete fully without severe cracking.

Applications

Creep on the underside of a cardboard box: a largely empty box was placed on a smaller box, and more boxes were placed on top of it. Due to the weight, the portions of the empty box not upheld by the lower support gradually deflected downward.

Though mostly due to the reduced yield strength at higher temperatures, the collapse of the World Trade Center was due in part to creep from increased temperature.

The creep rate of hot pressure-loaded components in a nuclear reactor at power can be a significant design constraint, since the creep rate is enhanced by the flux of energetic particles.

Creep in epoxy anchor adhesive was blamed for the Big Dig tunnel ceiling collapse in Boston, Massachusetts, that occurred in July 2006.

The design of tungsten light bulb filaments attempts to reduce creep deformation. Sagging of the filament coil between its supports increases with time due to the weight of the filament itself. If too much deformation occurs, the adjacent turns of the coil touch one another, causing local overheating, which quickly leads to failure of the filament. The coil geometry and supports are therefore designed to limit the stresses caused by the weight of the filament, and a special tungsten alloy with small amounts of oxygen trapped in the crystallite grain boundaries is used to slow the rate of Coble creep.

Creep can cause gradual cut-through of wire insulation, especially when stress is concentrated by pressing insulated wire against a sharp edge or corner. Special creep-resistant insulations such as Kynar (polyvinylidene fluoride) are used in wirewrap applications to resist cut-through due to the sharp corners of wire wrap terminals. Teflon insulation is resistant to elevated temperatures and has other desirable properties, but is notoriously vulnerable to cold-flow cut-through failures caused by creep.

In steam turbine power plants, pipes carry steam at high temperatures (566 °C, 1,051 °F) and pressures (above 24.1 MPa, 3,500 psi). In jet engines, temperatures can reach up to 1,400 °C (2,550 °F) and initiate creep deformation in even advanced-design coated turbine blades. Hence, it is crucial for correct functionality to understand the creep deformation behavior of materials.

Creep deformation is important not only in systems where high temperatures are endured such as nuclear power plants, jet engines and heat exchangers, but also in the design of many everyday objects. For example, metal paper clips are stronger than plastic ones because plastics creep at room temperatures. Aging glass windows are often erroneously used as an example of this phenomenon: measurable creep would only occur at temperatures above the glass transition temperature around 500 °C (932 °F). While glass does exhibit creep under the right conditions, apparent sagging in old windows may instead be a consequence of obsolete manufacturing processes, such as that used to create crown glass, which resulted in inconsistent thickness.

Fractal geometry, using a deterministic Cantor structure, is used to model the surface topography, where recent advancements in thermoviscoelastic creep contact of rough surfaces are introduced. Various viscoelastic idealizations are used to model the surface materials, including the Maxwell, Kelvin–Voigt, standard linear solid and Jeffrey models.

Nimonic 75 has been certified by the European Union as a standard creep reference material.

The practice of tinning stranded wires to facilitate the process of connecting the wire to a screw terminal, though having been prevalent and considered standard practice for quite a while, has been discouraged by professional electricians, owing to the fact that the solder is likely to creep under the pressure exerted on the tinned wire end by the screw of the terminal, causing the joint to lose tension and hence create a loose contact over time. The accepted practice when connecting stranded wire to a screw terminal is to use a wire ferrule on the end of the wire.

Prevention

Generally, materials have better creep resistance if they have higher melting temperatures, lower diffusivity, and higher shear strength. Close-packed structures are usually more creep resistant as they tend to have lower diffusivity than non-close-packed structures. Common methods to reduce creep include:

• Solid solution strengthening: adding other elements in solid solution can slow diffusion, as well as slow dislocation motion via the mechanism of solute drag.
• Particle dispersion strengthening: adding particles, often incoherent oxide or carbide particles, block dislocation motion.
• Precipitation hardening: precipitating a second phase out of the primary lattice blocks dislocation motion.
• Grain size: increasing grain size decreases the amount of grain boundaries, which results in slower creep due to the high diffusion rate along grain boundaries. This is opposite low-temperature applications, where increasing grain size decreases strength by blocking dislocation motion. In very high temperature applications such as jet engine turbines, single crystals are often used.

Superalloys

Materials operating at high temperatures, such as this nickel superalloy jet engine (RB199) turbine blade, must be able to withstand creep present at these temperatures.

Materials operating in high-performance systems, such as jet engines, often reach extreme temperatures surpassing 1,000 °C (1,830 °F), necessitating specialized material design. Superalloys based on cobalt, nickel, and iron have been engineered to be highly resistant to creep. The term ‘superalloy’ generally refers to austenitic nickel-, iron-, or cobalt-based alloys that use either γ′ or γ″ precipitation strengthening to maintain strength at high temperature.

The γ′ phase is a cubic L1₂-structure Ni
3(Al,Ti,Ta,Nb) phase that produces cuboidal precipitates. Superalloys often have a high (60–75%) volume fraction of γ′ precipitates. γ′ precipitates are coherent with the parent γ phase, and are resistant to shearing due to the development of an anti-phase boundary when the precipitate is sheared. The γ″ phase is a tetragonal Ni₃Nb or Ni₃V structure. The γ″ phase, however, is unstable above 650 °C (1,202 °F), so γ″ is less commonly used as a strengthening phase in high temperature applications. Carbides are also used in polycrystalline superalloys to inhibit grain boundary sliding.

Many other elements can be added to superalloys to tailor their properties. They can be used for solid solution strengthening, to reduce the formation of undesirable brittle precipitates, and to increase oxidation or corrosion resistance. Nickel-based superalloys have found widespread use in high-temperature, low stress applications. Iron-based superalloys are generally not used at high temperatures as the γ′ phase is not stable in the iron matrix, but are sometimes used at moderately high temperatures, as iron is significantly cheaper than nickel. Cobalt-based γ′ structure was found in 2006, allowing the development of cobalt-based superalloys, which are superior to nickel-based superalloys in corrosion resistance. However, in the base (cobalt–tungsten–aluminum) system, γ′ is only stable below 900 °C (1,650 °F), and cobalt-based superalloys tend to be weaker than their Ni counterparts.

Contributing factors in creep resistivity

1. Stages of creep

Based on the description of creep mechanisms and its three different stages mentioned earlier, creep resistance generally can be accomplished by using materials in which their tertiary stage is not active since, at this stage, the strain rate increases significantly by increasing stress. Therefore, a sound component design should satisfy the primary stage of creep, which has a relatively high initial creep rate that decreases with increasing exposure time, leading to the second stage of creep, in which the creep rate in the material is decelerated and reaches its minimum value via work hardening. The minimum value of creep rate is actually a constant creep rate, which plays a crucial role in designing a component, and its magnitude depends on temperature and stress. The minimum value of creep rate that is commonly applied to alloys is based on two norms: (1) the stress required to produce a creep rate of 0.1%/h×10⁻³ and (2) the stress required to produce a creep rate of 0.1%/h×10⁻⁴, which takes roughly about 11.5 years. The former standard has widely been used in the component design of turbine blades, while the latter is frequently used in designing steam turbines. One of the primary goals of creep tests is to determine the minimum value of the creep rate at the secondary stage and also to investigate the time required for an ultimate failure of a component. However, when it comes to ceramic applications, there are no such standards to determine their minimum creep rates, but it's safe to say that ceramics are usually picked up to operate at high-temperature applications under loads mainly because they possess a long lifetime. However, by acquiring information obtained from creep tests, proper ceramic material(s) can be selected for desired application to assure the safe service and evaluate the time period of secure service in high-temperature environments that the structural thermostability is essential. Therefore, by making the proper choice, suitable ceramic components may be selected, capable of operating at various conditions of high temperature and creep deformation.

2. Materials selection

Generally speaking, the structure of materials is different from one another. Metallic materials have different structures compared to polymer or ceramics, and even within the same class of materials, different structures might have existed at different temperatures. The difference in the structure includes the difference in grains (for example, their sizes, shapes, distributions), their crystalline or amorphous nature, and even dislocation and/or vacancy contents that are prone to change following a deformation. So, since creep is a time-dependent process and differs from one material to another, all these parameters must be considered in materials selection for a specific application. For instance, materials with low-dislocation content are among the suitable candidates for creep resistance. In other words, the dislocation glide and climb can be reduced if the proper material is selected (for example, ceramic materials are very popular in this case). In terms of vacancies, it's noteworthy to mention that the vacancy content not only depends on the chosen material but also on the component's service temperature. Vacancy-diffusion-controlled processes that promote creep can be categorized into grain boundary diffusion (Coble creep) and lattice diffusion (Nabarro–Herring creep). Therefore, the properties of dislocations and vacancies, their distributions throughout the structure, and their potential change due to long-time exposure to stress and temperature must be considered seriously in materials selection for components design. Therefore, the role of dislocations, vacancies, wide range of obstacles that can retard the dislocation motion, including grain boundaries in polycrystalline materials, solute atoms, precipitates, impurities, and strain fields originating from other dislocations or their pile-ups which increase the lifetime of materials and make them more resistive with respect to creep are always at the top list of materials selection and component design. For instance, different types of vacancies in ceramic materials have different charges stemming from their dominant chemical boding. So, existing or newly-formed vacancies must be charge-balanced to maintain the overall neutrality of the final structure. Besides paying attention to individual dislocation and vacancy contents, the correlation between them is also worth exploring since dislocation's ability to climb depends heavily on how many vacancies are available in its vicinity. To recap, materials must be selected and developed that possess low dislocation and vacancy contents to have a practical creep resistance component.

3. Various working conditions

● Temperature

Creep is a phenomenon that is related to a material's melting point (Tm). Generally, a high lifetime is expected when we have a higher melting point, and the reason behind selecting materials with high melting points originates from the fact that diffusion processes are related to temperature-dependent vacancy concentrations. The diffusion rate is slower in high-temperature materials. Ceramic materials are well known for having high melting points, and that's the reason why ceramics gravitated considerable attention to creep resistance applications. Although it's widely known that creep starts at a temperature equal to 0.5Tm, the safe temperature to avoid the initiation of creep is 0.3Tm. Creep that starts below or at 0.5Tm is called "low temperature creep" because diffusion is not very progressive at such low temperatures, and the kind of creep that occurs is not diffusion-dominant and is related to other mechanisms.
● Time

As mentioned previously, creep is a time-dependent deformation. Fortunately, creep doesn't occur suddenly in brittle materials as it does under tension and other forms of deformation, and it's an advantage for designers. Over time, creep strain develops in a material that is exposed to stress at the temperature of the application, and it depends on the duration of the exposure. Thus, besides temperature and stress, the creep rate is also a function of time, and it can be generalized as this function ε = F(t, T, σ) that tells the designer all the three parameters, including time, temperature, and stress acting in concert, and all of them must be considered if a successful creep-resistance component is to be attained.

See also

• Biomaterial
• Biomechanics
• Ductile–brittle transition temperature in materials science
• Deformation mechanism
• Downhill creep
• Hysteresis
• Larson–Miller parameter
• Stress relaxation
• Viscoelasticity
• Viscoplasticity
• Brittle–ductile transition zone

Further reading

• Ashby, Michael F.; Jones, David R. H. (1980). Engineering Materials 1: An Introduction to their Properties and Applications. Pergamon Press. ISBN 978-0-08-026138-6. https://archive.org/details/unset0000unse_h3q3. 
• Frost, Harold J. (1982). Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics. Pergamon Press. ISBN 978-0-08-029337-0. 
• Turner, S (2001). Creep of Polymeric Materials. Oxford: Elsevier Science Ltd.. pp. 1813–1817. ISBN 978-0-08-043152-9.