Earth:Lagrangian Ocean Analysis
Lagrangian ocean analysis is a way of analysing ocean dynamics by computing the trajectories of virtual fluid particles, following the Lagrangian perspective of fluid flow, from a specified velocity field. Often, the Eulerian velocity field used as an input for Lagrangian ocean analysis has been computed using an ocean general circulation model (OGCM).[1] Lagrangian techniques can be employed on a range of scales, from modelling the dispersal of biological matter within the Great Barrier Reef[2] to global scales.[3] Lagrangian ocean analysis has numerous applications, from modelling the diffusion of tracers,[1] through the dispersal of aircraft debris[4] and plastics,[5] to determining the biological connectivity of ocean regions.[2]
Techniques
Lagrangian ocean analysis makes use of the relation between the Lagrangian and Eulerian specifications of the flow field, namely [math]\displaystyle{ \mathbf{u}(\mathbf{x}, t) = \mathbf{u}(\mathbf{X}(\mathbf{x_0}, t), t) = \frac{\partial\mathbf{X}(\mathbf{x_0}, t)}{\partial t}, }[/math] where [math]\displaystyle{ \mathbf{X}(\mathbf{x_0}, t) }[/math] defines the trajectory of a particle (fluid parcel), labelled [math]\displaystyle{ \mathbf{x_0} }[/math], as a function of the time [math]\displaystyle{ t }[/math], and the partial derivative is taken for a given fluid parcel [math]\displaystyle{ \mathbf{x_0} }[/math].[6] In this context, [math]\displaystyle{ \mathbf{x_0} }[/math] is used to identify a given virtual particle - physically it corresponds to the position through which that particle passed at time [math]\displaystyle{ t_0 }[/math]. In words, this equation expresses that the velocity of a fluid parcel at the position along its trajectory that it reaches at time [math]\displaystyle{ t }[/math] can also be interpreted as the velocity at that point in the Eulerian coordinate system. Using this relation, the Eulerian velocity field can be integrated in time to trace a trajectory, [math]\displaystyle{ \mathbf{X}(t+\Delta t) = \mathbf{X}(t) + \int^{t+\Delta t}_{t}\mathbf{u}(\mathbf{X}(\mathbf{x_0}, t^\prime), t^\prime)dt^\prime, }[/math] where [math]\displaystyle{ t^\prime }[/math] is a dummy integration variable. In this equation, [math]\displaystyle{ \mathbf{u} }[/math] is continuous in space – for the integration of trajectories in a Lagrangian ocean model, the velocity field must be evaluable at any point in space. Spatial interpolation is used so that the velocity field can be evaluated at points inside the grid cells outputted by OGCMs.

Time Integration
In some cases, the time integration is performed using explicit time-stepping methods. Lagrangian ocean analysis codes may make use of, for instance, an Euler method, or a higher order method, such as Runge-Kutta 4 or Runge-Kutta 4-5.[1] If the timestep of the integration method is shorter than the time resolution of the Eulerian velocity field used as an input, then the velocity field must be interpolated in the temporal domain, so that there is a velocity value to be integrated for each time.
To ensure volume conservation in integrating the trajectories, symplectic methods, can be used. These methods are generally implicit in nature, requiring extra computation when compared to explicit methods.[7]
Alternatively, if each component of the flow velocity within a spatial grid is assumed to vary linearly along its axis, trajectories can be analytically calculated. If the velocity field is steady-state, then trajectories can be treated as streamlines, and considered together in bundles known as stream tubes, which bound fluid flow in different parts of the spatial domain.[8] If the velocity field provided as the starting point of the Lagrangian analysis is a divergence-free flow, the volume of fluid moving through a stream tube is conserved throughout the stream tube. To show this mathematically, the starting point is the condition that the divergence of the velocity field is zero, [math]\displaystyle{ \nabla\cdot\mathbf{u} = 0 . }[/math] Integrating this over the volume of a stream tube, the divergence theorem can be used to show that
- [math]\displaystyle{ \iiint_V\left(\mathbf{\nabla}\cdot\mathbf{u}\right)\,dV= }[/math]
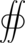 [math]\displaystyle{ \scriptstyle S }[/math] [math]\displaystyle{ (\mathbf{u}\cdot\mathbf{\hat{n}})\,dS = 0, }[/math]
[math]\displaystyle{ \scriptstyle S }[/math] [math]\displaystyle{ (\mathbf{u}\cdot\mathbf{\hat{n}})\,dS = 0, }[/math]
where [math]\displaystyle{ \mathbf{\hat{n}} }[/math] is the normal to the surface of the stream tube, [math]\displaystyle{ V }[/math] denotes the entire volume of the stream tube and [math]\displaystyle{ S }[/math] its surface. If the streamlines and pathlines (trajectories) are equivalent, as is the case for steady-state (non time-evolving) flows, then the walls of the stream tube do not contribute to the integral, as the flow cannot cross them. Thus, only the ends, [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_2 }[/math] will contribute to the integral, so [math]\displaystyle{ \iint_{S_1}(\mathbf{u}\cdot\mathbf{\hat{n}})\,dS + \iint_{S_2}(\mathbf{u}\cdot\mathbf{\hat{n}})\,dS = 0. }[/math] Physically, this equation expresses that the fluid flux passing through the two ends of the streamtube are equal, demonstrating the volume conservation. The equation also shows that the area of each end of the stream tube is inversely proportional to the speed of the normal flow through it. These features of the analytical method of calculating trajectories lend themselves to Lagrangian analyses primarily concerned with the advective (as opposed to diffusive) component of the flow. There exists a caveat to this approach: given that the velocity fields considered can be time-evolving, the equivalence between stream tubes and material pathways may not hold. Lagrangian ocean models can address this formalism by considering the flow field to be a piecewise function in the temporal domain, where each sub-function is a steady-state velocity field. A Boussinesq model, in which flow is incompressible and thus non-divergent,[9] can be used to generate the velocity field used as an input for the Lagrangian analysis code to ensure volume is conserved when using this method.
Incorporating Diffusion
For a Lagrangian ocean analysis code to include the effects of molecular diffusion, or other small-scale mixing which may be modelled as a diffusive process, stochastic terms must be added to the trajectory computations. Stochastic terms may be added in accordance with a stochastic differential equation (SDE) derived from the tracer diffusion equation in the form of the Fokker-Planck equation. This method requires that a diffusion tensor be provided.[1]
Rather than using an SDE derived with a diffusion tensor, Lagrangian ocean models may instead find an SDE based on how well the resulting diffusivity statistics fit either observations or models built with a finer resolution. This method involves the use of a Markov chain; the order of the Markov chain used is another point where different Lagrangian analysis codes differ.[1]
Online and Offline Analysis
Lagrangian ocean analysis codes can be characterised as online or offline. Online codes work in tandem with the Eulerian model that outputs the velocity field: each time the Eulerian model updates, the trajectories are timestepped using the new velocity information. The Lagrangian analysis packages available with some OGCMs are examples of online Lagrangian ocean analysis codes. Offline codes calculate trajectories using stored velocity fields outputted by Eulerian models at a prior stage. As a result of this, offline models may be used to calculate trajectories forwards or backwards through time; the latter may be helpful in determining the origins of water masses. As of 2018, there are no examples of online models that use the tracer equation to compute diffusive effects.[1]
Applications
One strength of Lagrangian ocean models is that they can be less computationally expensive than calculating the advection diffusion of a tracer concentration within the Eulerian paradigm: for each timestep, the Lagrangian code needs only evaluate the position of each virtual particle, as opposed to the Eulerian model which must explicitly calculate the tracer concentration in every grid cell.[1] In the case of offline models, trajectories may be advected backwards in time which can be useful in finding sources of the material being tracked.
Lagrangian ocean analysis has found use in tracking water masses, for instance tracking the source and pathways of the Subantarctic Mode Water, as well as how its temperature and salinity evolve along its path.[10] Another application of Lagrangian modelling techniques is in simulating the dispersal of biological matter in different ocean regions to gauge their biological connectivity.[2]
Lagrangian ocean analysis has also been used to model the dispersal of materials originating in human activities, for example in tracking the spread of oil following the 2010 Deepwater Horizon oil spill[11] and in attempts to model dispersal of Debris from flight MH370 in the Indian Ocean since 2014.[4] Furthermore, Lagrangian ocean analysis has played a role in the tracking of the transport of plastics across the global ocean, for instance helping researchers estimate the fraction of plastic debris that ends up at the coast.[12][13]
Examples
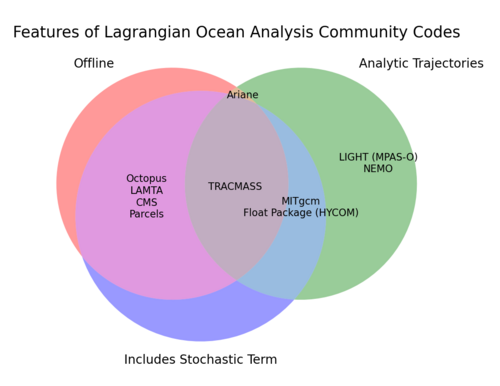
While small scale Lagrangian analysis codes have been written for many individual research projects, there exists a smaller number of community codes that can implement Lagrangian ocean models on a global scale.[1] The differences between 10 such community codes are illustrated in the venn diagram, where they are grouped in terms of whether they are offline, whether they include a stochastic term to model diffusion or small-scale turbulent mixing, and whether they compute trajectories analytically. All of the codes in the diagram that lie outside of the analytic trajectories circle employ explicit integration methods to compute the trajectories. Ariane, for example, is a code that runs offline, calculates trajectories with the analytic streamtube method and does not model diffusive effects.[1][3] By contrast, Parcels computes particle trajectories through explicit time-stepping and can include stochastic terms if the user desires; it is also offline.[1][14] A caveat to this is that Parcels' integration framework is customisable, and could be reprogrammed to instead use the analytical method to calculate trajectories.[14]
See also
- Lagrangian and Eulerian specification of the flow field
- Lagrangian analysis
- Lagrangian particle tracking
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 van Sebille, Erik; Griffies, Stephen M.; Abernathey, Ryan; Adams, Thomas P.; Berloff, Pavel; Biastoch, Arne; Blanke, Bruno; Chassignet, Eric P. et al. (1 January 2018). "Lagrangian ocean analysis: Fundamentals and practices". Ocean Modelling 121: 49–75. doi:10.1016/j.ocemod.2017.11.008. Bibcode: 2018OcMod.121...49V.
- ↑ 2.0 2.1 2.2 Thomas, Christopher J.; Lambrechts, Jonathan; Wolanski, Eric; Traag, Vincent A.; Blondel, Vincent D.; Deleersnijder, Eric; Hanert, Emmanuel (24 January 2014). "Numerical modelling and graph theory tools to study ecological connectivity in the Great Barrier Reef". Ecological Modelling 272: 160–174. doi:10.1016/j.ecolmodel.2013.10.002.
- ↑ 3.0 3.1 What is ARIANE? Retrieved 2021-05-18.
- ↑ 4.0 4.1 Durgadoo, Jonathan V.; Biastoch, Arne; New, Adrian L.; Rühs, Siren; Nurser, Aylmer J.G.; Drillet, Yann; Bidlot, Jean-Raymond (2 January 2021). "Strategies for simulating the drift of marine debris". Journal of Operational Oceanography 14 (1): 1–12. doi:10.1080/1755876X.2019.1602102.
- ↑ Lebreton, L. C. -M.; Greer, S. D.; Borrero, J. C. (1 March 2012). "Numerical modelling of floating debris in the world's oceans". Marine Pollution Bulletin 64 (3): 653–661. doi:10.1016/j.marpolbul.2011.10.027. PMID 22264500.
- ↑ Bennett, Andrew (2006). "Lagrangian Fluid Dynamics", Cambridge University Press. pp. 7.
- ↑ Holmes, M.H. (2007). "Introduction to Numerical Methods in Differential Equations". New York: Springer Science+Business Media, Llc. pp. 17
- ↑ Batchelor, G.K. (1967). "An Introduction to Fluid Dynamics", Cambridge University Press. pp. 72.
- ↑ Cushman-Roisin, Benoit and Beckers, Jean-Marie (2009). "Introduction to Geophysical Fluid Dynamics - Physical and Numerical Aspects", Academic Press. pp. 77.
- ↑ Koch-Larrouy, Ariane; Morrow, Rosemary; Penduff, Thierry; Juza, Mélanie (June 2010). "Origin and mechanism of Subantarctic Mode Water formation and transformation in the Southern Indian Ocean". Ocean Dynamics 60 (3): 563–583. doi:10.1007/s10236-010-0276-4. Bibcode: 2010OcDyn..60..563K.
- ↑ North, Elizabeth W.; Adams, E. Eric; Schlag, Zachary; Sherwood, Christopher R.; He, Ruoying; Hyun, Kyung Hoon; Socolofsky, Scott A. (2011). "Simulating Oil Droplet Dispersal from the Deepwater Horizon Spill with a Lagrangian Approach". Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record-Breaking Enterprise. Geophysical Monograph Series. 195. pp. 217–226. doi:10.1029/2011GM001102. ISBN 978-0-87590-485-6.
- ↑ Onink, Victor; Jongedijk, Cleo E; Hoffman, Matthew J; van Sebille, Erik; Laufkötter, Charlotte (1 June 2021). "Global simulations of marine plastic transport show plastic trapping in coastal zones". Environmental Research Letters 16 (6): 064053. doi:10.1088/1748-9326/abecbd. Bibcode: 2021ERL....16f4053O.
- ↑ Lebreton, Laurent; Egger, Matthias; Slat, Boyan (12 September 2019). "A global mass budget for positively buoyant macroplastic debris in the ocean". Scientific Reports 9 (1): 12922. doi:10.1038/s41598-019-49413-5. PMID 31515537. Bibcode: 2019NatSR...912922L.
- ↑ 14.0 14.1 Lange, Michael; van Sebille, Erik (17 November 2017). "Parcels v0.9: prototyping a Lagrangian ocean analysis framework for the petascale age". Geoscientific Model Development 10 (11): 4175–4186. doi:10.5194/gmd-10-4175-2017. Bibcode: 2017GMD....10.4175L.