Earth:Plate reconstruction

From HandWiki
Short description: Process of reconstructing the positions of tectonic plates in the geological past
This article describes techniques; for a history of the movement of tectonic plates, see Geological history of Earth.

Plate reconstruction is the process of reconstructing the positions of tectonic plates relative to each other (relative motion) or to other reference frames, such as the Earth's magnetic field or groups of hotspots, in the geological past. This helps determine the shape and make-up of ancient supercontinents and provides a basis for paleogeographic reconstructions.

Defining plate boundaries

Earthquake epicenters 1963–98

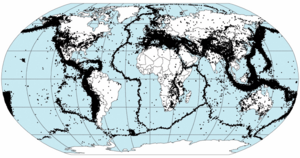
An important part of reconstructing past plate configurations is to define the edges of areas of the lithosphere that have acted independently at some time in the past.

Present plate boundaries

Most present plate boundaries are easily identifiable from the pattern of recent seismicity.[1] This is now backed up by the use of geodetic data, such as GPS/GNSS, to confirm the presence of significant relative movement between plates.[2]

Past plate boundaries

Identifying past (but now inactive) plate boundaries within current plates is generally based on evidence for an ocean that has now closed up. The line where the ocean used to be is normally marked by pieces of the crust from that ocean, included in the collision zone, known as ophiolites.[3] The line across which two plates became joined to form a single larger plate, is known as a suture.

In many orogenic belts, the collision is not just between two plates, but involves the sequential accretion of smaller terranes. Terranes are smaller pieces of continental crust that have been caught up in an orogeny, such as continental fragments or island arcs.

Reference frames

Plate motions, both those observable now and in the past, are referred ideally to a reference frame that allows other plate motions to be calculated. For example, a central plate, such as the African plate, may have the motions of adjacent plates referred to it. By composition of reconstructions, additional plates can be reconstructed to the central plate. In turn, the reference plate may be reconstructed, together with the other plates, to another reference frame, such as the Earth's magnetic field, as determined from paleomagnetic measurements of rocks of known age. A global hotspot reference frame has been postulated (see, e.g., W. Jason Morgan) but there is now evidence that not all hotspots are necessarily fixed in their locations relative to one another or the Earth's spin axis.[4] However, there are groups of such hotspots that appear to be fixed within the constraints of available data, within particular mesoplates.[5]

Euler poles

The movement of a rigid body, such as a plate, on the surface of a sphere can be described as rotation about a fixed axis (relative to the chosen reference frame). This pole of rotation is known as an Euler pole. The movement of a plate is completely specified in terms of its Euler pole and the angular rate of rotation about the pole. Euler poles defined for current plate motions can be used to reconstruct plates in the recent past (few million years).[6] At earlier stages of Earth's history, new Euler poles need to be defined.[4]

Estimating past plate motions

Ages of oceanic lithosphere

In order to move plates backward in time it is necessary to provide information on either relative or absolute positions of the plates being reconstructed such that an Euler pole can be calculated. These are quantitative methods of reconstruction.[7]

Geometric matching of continental borders

Certain fits between continents, particularly that between South America and Africa, were known long before the development of a theory that could adequately explain them. The reconstruction before Atlantic rifting by Bullard based on a least-squares fitting at the 500 fathom contour still provides the best match to paleomagnetic pole data for the two sides from the middle of Paleozoic to Late Triassic.[7]

Plate motion from magnetic stripes

Plate reconstructions in the recent geological past mainly use the pattern of magnetic stripes in oceanic crust to remove the effects of seafloor spreading. The individual stripes are dated from magnetostratigraphy so that their time of formation is known. Each stripe (and its mirror image) represents a plate boundary at a particular time in the past, allowing the two plates to be repositioned relative to one another. The oldest oceanic crust is Jurassic, providing a lower age limit of about 175 Ma for the use of such data. Reconstructions derived in this way are only relative.[7]

Plate reconstructions from paleomagnetism

Paleomagnetic data: Sampling

Paleomagnetic data are obtained by taking oriented samples of rocks and measuring their remanent magnetizations in the laboratory. Good quality data can be recovered from different rock types. In igneous rocks, magnetic minerals crystallize from the melt, and when the rock is cooled below their Curie temperature, it acquires a thermoremanent magnetization (TRM) in the direction of the Earth's magnetic field. In sedimentary rocks, magnetic grains will align their magnetic moments with the direction of the magnetic field during or soon after the deposition, resulting in a detrital or post-detrital remanent magnetization (DRM). A common difficulty with the use of clastic sediments for defining directions of the magnetic field in the past is that the direction of DRM may rotate toward the bedding plane due to the compaction of sediment, resulting in an inclination, which is shallower than the inclination of the field during the deposition. The inclination flattening error can nevertheless be estimated and corrected for through re-deposition experiments, measurements of magnetic anisotropy, and the use of theoretical models for the dispersion of paleomagnetic directions.[8] Metamorphic rocks are not normally used for paleomagnetic measurements due to the complexities related to the acquisition of remanence, uncertainties in magnetization age, and high magnetic anisotropy.

A typical paleomagnetic study would sample a large number of independent rock units of similar age at nearby locations and collect multiple samples from each unit in order to estimate measurement errors and assess how well the obtained paleomagnetic dataset samples geomagnetic secular variation. Progressive demagnetization techniques are used to identify secondary magnetization components (e.g., magnetic overprints that could have been imparted on the rock due to chemical alteration or reheating) and to isolate the primary magnetization, which records the direction of the magnetic field at the time when the rock was formed. Various rock-magnetic and paleomagnetic tests are normally performed to establish the primary nature of the isolated remanent magnetization. The recovered paleomagnetic directions are used to derive paleomagnetic poles, which provide constrains on the latitudinal position of the crustal block from which the rock samples were taken, and its original orientation with respect to the lines of longitude.

Good quality paleomagnetic data are available from the Global Paleomagnetic Database, which is accessible from the World Data Center A in the US at Boulder, Colorado.[9]

Paleomagnetic poles

A paleomagnetic pole is defined by taking the average direction of the primary remanent magnetization for the sampled rocks (expressed as the mean declination and inclination) and calculating the position of a geomagnetic pole for the field of a geocentric magnetic dipole that would produce the observed mean direction at the sampled locality in its present geographic coordinates.[10] An alternative way of defining paleomagnetic poles is to calculate a virtual geomagnetic pole (VGP) for each individual rock unit and then estimate the mean location for all VGPs. Fisher statistics on the sphere[11] is normally used to obtain the mean direction of magnetization, or the mean VGP location, and to estimate their uncertainties. Both approaches are used in paleomagnetic studies, but it has been recognized that averaging directions instead of full remanence vectors can lead to biased estimates of the mean direction of the paleomagnetic field,[12] so that the calculation of paleomagnetic poles by averaging VGPs is currently the preferred technique.

Applications to paleogeographic reconstructions

Paleogeographic reconstruction of the Pangea supercontinent at the Permo-Triassic Boundary (250 Ma). Top panel: Synthetic APWP for Africa (the south paleomagnetic poles are shown with their 95% uncertainty ovals). The red dot highlights the 250 Ma paleomagnetic pole. APWP data are from Torsvik et al. (2012).[13] Middle panel: All continents are assembled in the Pangea configuration at 250 Ma using the estimates of their relative motions, with Africa kept fixed in its present position. The red triangle shows the position of the Euler pole and the red arrow indicates the rotation that would reconstruct the paleomagnetic pole to the south geographic pole. Bottom panel: The Euler rotation has been applied to Pangea, which is now reconstructed paleogeographically. The longitude is arbitrary set to minimize the longitudinal motion of Africa since 250 Ma.

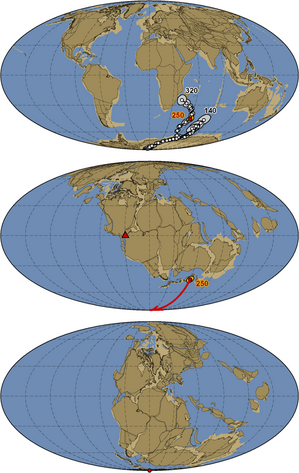
Paleomagnetic studies of geologically recent lavas (Pliocene to Quaternary, 0-5 Ma) indicate that when the geomagnetic field is averaged on time scales of tens of thousands to millions of years – over a time period long enough to fully sample geomagnetic secular variation, the time-averaged field can be accurately approximated by the field of a geocentric axial dipole (GAD) – that is, a magnetic dipole placed in the center of the Earth and aligned with the Earth's rotation axis.[14][15] Hence, if a paleomagnetic dataset has sampled enough time to average secular variation, the paleomagnetic pole derived from it can be interpreted as an estimate for the location of the geographic pole with respect to the sampling locality fixed in the present geographic position.

The difference between the paleomagnetic pole and the present geographic pole reflects the paleogeographic position of the crustal block containing the sampled area at the time when the studied rocks were formed, including its original latitude (paleolatitude) and orientation. Under the assumption that the mean paleomagnetic direction corresponds to that of the GAD field, the paleolatitude of the sampling location (λ) can be derived from the inclination (I) of the mean direction using a simple equation:[16]

[math]\displaystyle{ \tan(\lambda)=\frac{1}{2}\cdot \tan(I) }[/math]

The mean declination (D) gives the sense and amount of rotation about a vertical axis passing through the sampling area, which needs to be applied to restore its original orientation with respect to the lines of longitude. The paleolatitude for any specific location belonging to the same crustal block can be computed as 90° minus the angular distance between this location and the paleomagnetic pole, and the local vertical axis rotation can be estimated by computing the declination expected from the position of the pole.[17] Thus, a paleomagnetic pole defines the paleo-latitudinal position and orientation of the entire tectonic block at a specific time in the past. However, because the GAD field is azimuthally symmetric about the Earth's rotation axis, the pole does not set any constraint on the absolute longitude. From the perspective of paleomagnetic directions, the GAD field has the same values of inclination and declination along a line of constant latitude at all longitudes, so that any conceivable longitude would be an equally viable option for the reconstruction of a tectonic element if its paleogeographic position is constrained by paleomagnetic data alone.

Considering that a paleomagnetic pole approximates the position of the geographic pole with respect to the continent or geologic terrane from which it was determined, the paleolatitude and orientation can be restored by finding a rotation (Euler pole and rotation angle) that reconstructs the paleomagnetic pole to the geographic pole, and applying this rotation to the continent or terrane. By doing so, the crustal block and its paleomagnetic pole are reconstructed using the same Euler rotation, so that they do not move relative to each other, the paleomagnetic pole is placed at the geographic pole, and the crustal block is correctly restored in latitude and orientation (i.e., with respect to the geographic pole). Noting that a further rotation around the geographic pole will only change the longitude of the block, but its latitude and orientation with respect to the lines of longitude will not be affected, the absolute paleolongitude cannot be determined in reconstructions based on paleomagnetism. However, relative longitudes of different crustal blocks can be defined using other types of geological and geophysical data constraining relative motions of tectonic plates, including the histories of seafloor spreading recorded my marine magnetic anomalies, matching of continental borders and geologic terranes, and paleontological data.[7]

Apparent polar wander paths

Main page: Physics:Apparent polar wander

Poles from different ages in a single continent, lithospheric plate, or any other tectonic block can be used to construct an apparent polar wander path (APWP). If paths from adjacent crustal fragments are identical, this is taken to indicate that there has been no relative movement between them during the period covered by the path. Divergence of APW paths indicates that the areas in question have acted independently in the past with the point of divergence marking the time at which they became joined.[17] Combined or synthetic APWPs can be constructed by rotating paleomagnetic poles from different plates into the reference frame fixed to a single plate, using estimates of relative plate motions.[13] For the times postdating the assembly of Pangea (320 Ma), synthetic APWPs are often constructed in the reference frame fixed to the African plate[13] because Africa has occupied a central position in the Pangea configuration and has been dominantly surrounded by spreading ridges after the Pangea breakup, which commenced in the early Jurassic (ca. 180 Ma).

Longitude constraints

For a single lithospheric plate, the APWP reflects the motion of the plate with respect to the geographic pole (changes in latitude) and changes of its orientation with respect to paleomeridians. The longitudes of paleogeographic reconstructions based on APWPs are uncertain, but it has been argued that the uncertainty can be minimized by selecting a reference plate that is expected to move the least in longitude from the consideration of the plate tectonics theory and by linking the reconstructions of the remaining plates to this reference plate using the estimates of relative plate motion.[18] For example, and it was shown that assuming no significant longitudinal motion of Africa since the time of the Pangea assembly results in a reasonable plate tectonic scenario, in which no large, coherent east-west motions of the continental lithosphere are observed in paleogeographic reconstructions.[19]

APWPs can be interpreted as records of a combined signal from two sources of plate motion: (1) motion of lithospheric plates with respect to the Earth's mantle and (2) motion of the entire solid Earth (mantle and lithosphere) with respect to the Earth's rotation axis. The second component is commonly referred to as true polar wander (TPW) and on geologic time scales results from gradual redistribution of mass heterogeneities due to convective motions in the Earth's mantle.[20] By comparing plate reconstructions based on paleomagnetism with reconstructions in the mantle reference frame defined by hotspots for the last 120 Ma, the TPW motions can be estimated, which allows tying paleogeographic reconstructions to the mantle and hence constraining them in paleolongitude.[21][13] For the earlier times in the Mesozoic and Paleozoic, TPW estimates can be obtained through the analysis of coherent rotations of the continental lithosphere,[19] which allows linking the reconstructed paleogeography to the large-scale structures in the lower mantle, commonly referred to as Large Low Shear-wave Velocity Provinces (LLSVPs). It has been argued that the LLSVPs have been stable over at least the past 300 Ma, and possibly longer, and that the LLSVP margins have served as generation zones for the mantle plumes responsible for eruptions of Large Igneous Provinces (LIPs) and kimberlites.[22][23] Correlating the reconstructed locations of LIPs and kimberlites with the margins of LLSVPs using the estimated TPW rotations makes it possible to develop a self-consistent model for plate motions relative to the mantle, true polar wander, and the corresponding changes of paleogeography constrained in longitude for the entire Phanerozoic,[24] although the origin and long-term stability of LLSVPs are the subject of the ongoing scientific debate.[25][26]

Apparent polar wander paths geometric parameterizations

Paleomagnetic Euler poles derived by geometrizing apparent polar wander paths (APWPs) potentially allows constraining paleolongitudes from paleomagnetic data. This method could extend absolute plate motion reconstructions deeply into the geologic history as long as there are reliable APWPs.[27]

Hotspot tracks

The Hawaiian-Emperor seamount chain

The presence of chains of volcanic islands and seamounts interpreted to have formed from fixed hotspots allows the plate on which they sit to be progressively restored so that a seamount is moved back over the hotspot at its time of formation. This method can be used back to the Early Cretaceous, the age of the oldest evidence for hotspot activity. This method gives an absolute reconstruction of both latitude and longitude, although before about 90 Ma there is evidence of relative motion between hotspot groups.[28]

Slab constraints

Once oceanic plates subduct in the lower mantle (slabs), they are assumed to sink in a near-vertical manner. With the help of seismic wave tomography, this can be used to constrain plate reconstructions at first order back to the Permian.[29]

Other evidence for past plate configurations

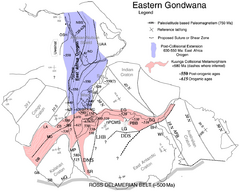
Reconstruction of eastern Gondwana showing position of orogenic belts

Some plate reconstructions are supported by other geological evidence, such as the distribution of sedimentary rock types, the position of orogenic belts and faunal provinces shown by particular fossils. These are semi-quantitative methods of reconstruction.[7]

Sedimentary rock types

Some types of sedimentary rock are restricted to certain latitudinal belts. Glacial deposits for instance are generally confined to high latitudes, whereas evaporites are generally formed in the tropics.[30]

Faunal provinces

Oceans between continents provide barriers to plant and animal migration. Areas that have become separated tend to develop their own fauna and flora. This is particularly the case for plants and land animals but is also true for shallow water marine species, such as trilobites and brachiopods, although their planktonic larvae mean that they were able to migrate over smaller deep water areas. As oceans narrow before a collision occurs, the faunas start to become mixed again, providing supporting evidence for the closure and its timing.[7]

Orogenic belts

When supercontinents break up, older linear geological structures such as orogenic belts may be split between the resulting fragments. When a reconstruction effectively joins up orogenic belts of the same age of formation, this provides further support for the reconstruction's validity.[7]

See also

  • General
    • Consilience, evidence from independent, unrelated sources can "converge" on strong conclusions

References

  1. ↑ Condie, K.C. (1997). Plate tectonics and crustal evolution (4th ed.). Butterworth-Heinemann. pp. 282. ISBN 978-0-7506-3386-4. https://books.google.com/books?id=QfhGuFwi0DgC&q=identification+%22plate+boundaries%22&pg=PA6. Retrieved 2010-02-21. 
  2. ↑ "Measuring plate motion with geodesy - Earth 520: Plate Tectonics and People: Foundations of Solid Earth Science". https://www.e-education.psu.edu/earth520/content/l7_p7.html. 
  3. ↑ Lliboutry, L. (2000). Quantitative geophysics and geology. Springer. pp. 480. ISBN 978-1-85233-115-3. https://books.google.com/books?id=C7rny3qA6RMC&q=old+oceans+suture+ophiolites&pg=PA133. Retrieved 2010-02-22. 
  4. ↑ 4.0 4.1 Kearey, P.; Klepeis K.A.; Vine F.J. (2009). Global tectonics (3rd ed.). Wiley-Blackwell. pp. 482. ISBN 978-1-4051-0777-8. https://books.google.com/books?id=HYqZntfg25UC&q=indo+atlantic+hotspot+%22reference+frame%22&pg=PA102. 
  5. ↑ Pilger, R.H. (2003). Geokinematics: prelude to geodynamics. Springer. pp. 338. ISBN 9783540005483. https://books.google.com/books?id=PfX-o96Ou1wC&q=hotspot+%22reference+frame%22&pg=PA14. Retrieved 2010-02-21. 
  6. ↑ Carracedo, Juan Carlos; Troll, Valentin R. (2021-01-01), Alderton, David; Elias, Scott A., eds. (in en), North-East Atlantic Islands: The Macaronesian Archipelagos, Oxford: Academic Press, pp. 674–699, doi:10.1016/b978-0-08-102908-4.00027-8, ISBN 978-0-08-102909-1, https://www.sciencedirect.com/science/article/pii/B9780081029084000278, retrieved 2021-03-18 
  7. ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 Torsvik, T.H.. "Reconstruction Methods". http://www.geodynamics.no/GMAP/Methods/Introduction_to_Methods.htm. 
  8. ↑ Tauxe, L. (2005). "Inclination flattening and the geocentric axial dipole hypothesis" (in en). Earth and Planetary Science Letters 233 (3–4): 247–261. doi:10.1016/j.epsl.2005.01.027. ISSN 0012-821X. 
  9. ↑ National Geophysics Data Center (2010). "IAGA Paleomagnetic Databases". http://www.ngdc.noaa.gov/geomag/paleo.shtml. 
  10. ↑ Butler, R.F. (1992). Paleomagnetism: Magnetic Domains to Geologic Terranes, Chaper 7: Paleomagnetic Poles. Blackwell Scientific Publications. https://www.geo.arizona.edu/Paleomag/chap07.pdf. 
  11. ↑ Fisher, R. A. (1953). "Dispersion on a sphere" (in en). Proc. R. Soc. Lond. A 217 (1130): 295–305. doi:10.1098/rspa.1953.0064. ISSN 0080-4630. Bibcode: 1953RSPSA.217..295F. 
  12. ↑ Creer, K. M. (1983). "Computer synthesis of geomagnetic palaeosecular variations" (in En). Nature 304 (5928): 695–699. doi:10.1038/304695a0. ISSN 0028-0836. Bibcode: 1983Natur.304..695C. 
  13. ↑ 13.0 13.1 13.2 13.3 Torsvik, T.H. (2012). "Phanerozoic polar wander, palaeogeography and dynamics" (in en). Earth-Science Reviews 114 (3–4): 325–368. doi:10.1016/j.earscirev.2012.06.007. ISSN 0012-8252. Bibcode: 2012ESRv..114..325T. http://www.gt-crust.ru/jour/article/view/311. 
  14. ↑ Opdyke, N. D.; Kent, D. V.; Foster, D. A.; Huang, K. (2015). "Paleomagnetism of Miocene volcanics on Sao Tome: Paleosecular variation at the Equator and a comparison to its latitudinal dependence over the last 5 Myr" (in en). Geochemistry, Geophysics, Geosystems 16 (11): 3870–3882. doi:10.1002/2015gc005901. ISSN 1525-2027. Bibcode: 2015GGG....16.3870O. 
  15. ↑ McElhinny, Michael W.; McFadden, Phillip L. (1997). "Palaeosecular variation over the past 5 Myr based on a new generalized database" (in en). Geophysical Journal International 131 (2): 240–252. doi:10.1111/j.1365-246X.1997.tb01219.x. ISSN 0956-540X. Bibcode: 1997GeoJI.131..240M. 
  16. ↑ Butler, R.F. (1992). Paleomagnetism: Magnetic Domains to Geologic Terranes, Chapter 1: Introduction to Geomagnetism. Blackwell Scientific Publications. https://www.geo.arizona.edu/Paleomag/chap01.pdf. 
  17. ↑ 17.0 17.1 Butler, R.F. (1992). "Chapter 10 Applications to paleogeography". Paleomagnetism:Magnetic domains to geologic terranes. Blackwell. http://www.geo.arizona.edu/Paleomag/book/chap10.pdf. 
  18. ↑ Torsvik, T.H. (2008). "Longitude: Linking Earth's ancient surface to its deep interior" (in en). Earth and Planetary Science Letters 276 (3–4): 273–282. doi:10.1016/j.epsl.2008.09.026. ISSN 0012-821X. Bibcode: 2008E&PSL.276..273T. 
  19. ↑ 19.0 19.1 Steinberger, Bernhard; Torsvik, Trond H. (2008). "Absolute plate motions and true polar wander in the absence of hotspot tracks" (in En). Nature 452 (7187): 620–623. doi:10.1038/nature06824. ISSN 0028-0836. PMID 18385737. Bibcode: 2008Natur.452..620S. 
  20. ↑ Goldreich, Peter; Toomre, Alar (1969-05-15). "Some remarks on polar wandering" (in en). Journal of Geophysical Research 74 (10): 2555–2567. doi:10.1029/jb074i010p02555. ISSN 0148-0227. Bibcode: 1969JGR....74.2555G. 
  21. ↑ Doubrovine, Pavel V.; Steinberger, Bernhard; Torsvik, Trond H. (2012). "Absolute plate motions in a reference frame defined by moving hot spots in the Pacific, Atlantic, and Indian oceans" (in en). Journal of Geophysical Research: Solid Earth 117 (B9): B09101. doi:10.1029/2011jb009072. ISSN 0148-0227. Bibcode: 2012JGRB..117.9101D. 
  22. ↑ Torsvik, Trond H.; Burke, Kevin; Steinberger, Bernhard; Webb, Susan J.; Ashwal, Lewis D. (2010). "Diamonds sampled by plumes from the core–mantle boundary" (in En). Nature 466 (7304): 352–355. doi:10.1038/nature09216. ISSN 0028-0836. PMID 20631796. Bibcode: 2010Natur.466..352T. https://gfzpublic.gfz-potsdam.de/pubman/item/item_240963_1/component/file_240962/15256.pdf. 
  23. ↑ Torsvik, Trond H.; Voo, Rob van der; Doubrovine, Pavel V.; Burke, Kevin; Steinberger, Bernhard; Ashwal, Lewis D.; Trønnes, Reidar G.; Webb, Susan J. et al. (2014). "Deep mantle structure as a reference frame for movements in and on the Earth" (in en). Proceedings of the National Academy of Sciences 111 (24): 8735–8740. doi:10.1073/pnas.1318135111. ISSN 0027-8424. PMID 24889632. Bibcode: 2014PNAS..111.8735T. 
  24. ↑ Torsvik, T.H. (2018). "Earth history: A journey in time and space from base to top" (in en). Tectonophysics 760: 297–313. doi:10.1016/j.tecto.2018.09.009. ISSN 0040-1951. 
  25. ↑ Bower, Dan J.; Gurnis, Michael; Seton, Maria (2013). "Lower mantle structure from paleogeographically constrained dynamic Earth models" (in en). Geochemistry, Geophysics, Geosystems 14 (1): 44–63. doi:10.1029/2012gc004267. ISSN 1525-2027. Bibcode: 2013GGG....14...44B. 
  26. ↑ Bull, A.L. (2014). "The effect of plate motion history on the longevity of deep mantle heterogeneities" (in en). Earth and Planetary Science Letters 401: 172–182. doi:10.1016/j.epsl.2014.06.008. ISSN 0012-821X. Bibcode: 2014E&PSL.401..172B. 
  27. ↑ Wu, L.; Kravchinsky V.A. (2014). "Derivation of paleo-longitude from the geometric parametrization of apparent polar wander path: implication for absolute plate motion reconstruction". Geophysical Research Letters 41 (13): 4503–4511. doi:10.1002/2014GL060080. Bibcode: 2014GeoRL..41.4503W. 
  28. ↑ Torsvik, Trond Helge; Steinberger, Bernhard (December 2006). "Fra kontinentaldrift til manteldynamikk" (in no). Geo 8: 20–30. http://www.geodynamics.no/indexOld.htm. Retrieved 22 June 2010. , translation: Torsvik, Trond Helge; Steinberger, Bernhard (2008). "From Continental Drift to Mantle Dynamics". in Trond Slagstad. Geology for Society for 150 years - The Legacy after Kjerulf. 12. Trondheim: Norges Geologiske Undersokelse. pp. 24–38. http://www.geodynamics.no/guest/Torsvik_SteinbergerGraasteinen12.pdf. Retrieved 18 June 2010[Norwegian Geological Survey, Popular Science]. 
  29. ↑ van der Meer, D.G.; Spakman W.; van Hinsbergen D.J.J.; Amaru M.L.; Torsvik T.H. (2010). "Towards absolute plate motions constrained by lower-mantle slab remnants". Nature Geoscience 3 (1): 36–40. doi:10.1038/NGEO708. Bibcode: 2010NatGe...3...36V. http://www.geologist.nl/images/vanderMeer_2010.pdf. Retrieved 22 November 2011. 
  30. ↑ Scotese, C.R. (2002-04-20). "Climate History". Paleomap Project. http://www.scotese.com/climate.htm. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Earth:Plate_reconstruction&oldid=3296210"