Engineering:Antenna aperture

In electromagnetics and antenna theory, antenna aperture, effective area, or receiving cross section, is a measure of how effective an antenna is at receiving the power of electromagnetic radiation (such as radio waves). The aperture is defined as the area, oriented perpendicular to the direction of an incoming electromagnetic wave, which would intercept the same amount of power from that wave as is produced by the antenna receiving it. Assume a plane wave in a particular direction has an irradiance or power flux density [math]\displaystyle{ S }[/math]; this is the amount of power passing through a unit area of one square meter. Then if an antenna delivers [math]\displaystyle{ P_o }[/math] watts to the load connected to its output terminals (e.g. the receiver) when irradiated by a uniform field of power density [math]\displaystyle{ S }[/math] watts per square meter, the antenna's aperture for the direction of that plane wave is [math]\displaystyle{ A_e }[/math] in square meters, given by:

[math]\displaystyle{ A_e = \frac {P_o}{S} \, }[/math] .

So the power received by an antenna (in watts) is equal to the power density of the electromagnetic energy (in watts per square meter), multiplied by its aperture (in square meters). Radio waves from a direction where the antenna's aperture is larger thus collect a greater amount of that wave's power; this is more often referred to as antenna gain. To actually obtain that available power [math]\displaystyle{ P_o }[/math], the incoming radiation must be in the state of polarization specified for that antenna, and the load (receiver) must be impedance matched to the antenna's feedpoint impedance.

The meaning of aperture is thus based on a receiving antenna, however any receiving antenna can also be used for transmission. Due to reciprocity, an antenna's gain in receiving and transmitting are identical, so the power transmitted by an antenna in different directions (the radiation pattern) is always proportional to the effective area [math]\displaystyle{ A_e }[/math] in each direction; that proportionality factor is derived below. When no direction is specified, [math]\displaystyle{ A_e }[/math] (or "antenna gain") is understood to refer to its maximum value, that is, in the intended direction(s) that the antenna is designed to receive from and/or transmit toward.

Aperture efficiency

In general, the aperture of an antenna cannot be directly inferred from its physical size. However so-called aperture antennas such as parabolic dishes and horn antennas, have a large (relative to the wavelength) physical area [math]\displaystyle{ A_\text{phys} }[/math] which is opaque to such radiation, essentially casting a shadow from a plane wave and thus removing an amount of power [math]\displaystyle{ A_\text{phys} S }[/math] from the original beam. That power removed from the plane wave can be actually received by the antenna (converted into electrical power) or can be reflected or otherwise scattered, or can be absorbed (converted to heat). In this case the effective aperture [math]\displaystyle{ A_e }[/math] is always less than (or equal to) the area of the antenna's physical aperture [math]\displaystyle{ A_\text{phys} }[/math], as it accounts only for the portion of that wave actually received as electrical power. An aperture antenna's aperture efficiency, [math]\displaystyle{ e_a }[/math] is defined as the ratio of these two areas:

[math]\displaystyle{ e_a = {A_e \over A_\text{phys}} \, }[/math]

The aperture efficiency is a dimensionless parameter between 0 and 1.0 that measures how close the antenna comes to using all the radio wave power intersecting its physical aperture. If the aperture efficiency were 100% then all the wave's power falling on its physical aperture would be converted to electrical power delivered to the load attached to its output terminals, so these two areas would be equal [math]\displaystyle{ A_e = A_\text{phys} }[/math]. But due to nonuniform illumination by a parabolic dish's feed, as well as other scattering or loss mechanisms, this is not achieved in practice. Since a parabolic antenna's cost and wind load increase with the physical aperture size, there may be a strong motivation to reduce these (while achieving a specified antenna gain) by maximizing the aperture efficiency. Aperture efficiencies of typical aperture antennas vary from 0.35 to well over 0.70.

Note that when one simply speaks of an antenna's "efficiency," what is most often meant is the radiation efficiency, a measure which applies to all antennas (not just aperture antennas) and accounts only for the gain reduction due to losses. Outside of aperture antennas, most antennas consist of thin wires or rods with a small physical cross-sectional area (generally much smaller than [math]\displaystyle{ A_e }[/math]) for which "aperture efficiency" is not even defined.

Aperture and gain

The directivity of an antenna, its ability to direct radio waves preferentially in one direction or receive preferentially from a given direction, is expressed by a parameter called antenna gain [math]\displaystyle{ G }[/math]. This is most commonly defined as the ratio of the power [math]\displaystyle{ P_o }[/math] received by that antenna from waves in a given direction to the power [math]\displaystyle{ P_\text{iso} }[/math] that would be received by an ideal isotropic antenna, that is, a hypothetical antenna that receives power equally well from all directions. It can be seen that (for antennas at a given frequency) gain is also equal to the ratio of the apertures of these antennas

[math]\displaystyle{ G = {P_o \over P_\text{iso}} = {A_e \over A_\text{iso}} }[/math]

As shown below, the aperture of a lossless isotropic antenna, which by this definition has unity gain, is

[math]\displaystyle{ A_\text{iso} = {\lambda^2 \over 4 \pi} \, }[/math]

where [math]\displaystyle{ \lambda }[/math] is the wavelength of the radio waves. So

[math]\displaystyle{ G = {A_e \over A_\text{iso}} = {4\pi A_e \over \lambda^2} \, }[/math].

So antennas with large effective apertures are considered high gain antennas (or beam antennas), which have relatively small angular beam widths. As receiving antennas, they are much more sensitive to radio waves coming from a preferred direction compared to waves coming from other directions (which would be considered interference). As transmitting antennas, most of their power is radiated in a particular direction at the expense of other directions. Although antenna gain and effective aperture are functions of direction, when no direction is specified these are understood to refer to their maximum values, that is, in the direction(s) of the antenna's intended use (also referred to as the antenna's main lobe or boresight).

Friis transmission formula

The fraction of the power delivered to a transmitting antenna that is received by a receiving antenna is proportional to the product of the apertures of both the antennas and inversely proportional to the distance between the antennas and wavelength. This is given by a form of the Friis transmission formula:.

[math]\displaystyle{ \frac{P_r}{P_t} = \frac { A_r A_t }{ d^2 \lambda^2 }\, }[/math]

where:

• [math]\displaystyle{ P_t }[/math] is the power fed into the transmitting antenna input terminals;
• [math]\displaystyle{ P_r }[/math] is the power available at receiving antenna output terminals;
• [math]\displaystyle{ A_r }[/math] is the effective area of the receiving antenna;
• [math]\displaystyle{ A_t }[/math] is the effective area of the transmitting antenna;
• [math]\displaystyle{ d }[/math] is the distance between antennas. The formula is only valid for [math]\displaystyle{ d }[/math] large enough to ensure a plane wave front at the receive antenna, sufficiently approximated by [math]\displaystyle{ d \geqq 2a^2/\lambda }[/math] where [math]\displaystyle{ a }[/math] is the largest linear dimension of either of the antennas.
• [math]\displaystyle{ \lambda }[/math] is the wavelength of the radio frequency;

Effective length

Most antenna designs are not defined by a physical area but consist of wires or thin rods; then the effective aperture bears no clear relation to the size or area of the antenna. An alternate measure of antenna response that has a greater relationship to the physical length of such antennas is effective length l_eff measured in metres, which is defined for a receiving antenna as:

[math]\displaystyle{ l_\text{eff} = V_0 / E_s \, }[/math]

where

V₀ is the open circuit voltage appearing across the antenna's terminals

E_s is the electric field strength of the radio signal, in volts per metre, at the antenna.

The longer the effective length the greater is the voltage appearing at its terminals, however the actual power implied by that voltage depends on the antenna's feedpoint impedance, so this cannot be directly related to antenna gain which is a measure of received power (but does not directly specify voltage or current). For instance, a half-wave dipole has a much longer effective length than a short dipole. However the effective area of the short dipole is almost as great as it is for the half-wave antenna, since (ideally), given an ideal impedance matching network, it can receive almost as much power from that wave. Note that for a given antenna feedpoint impedance, an antenna's gain or A_eff increases according to the square of l_eff, so that the effective length for an antenna relative to different wave directions follows the square root of the gain in those directions. But since changing the physical size of an antenna inevitably changes the impedance (often by a great factor), the effective length is not, by itself, a useful figure of merit for describing an antenna's peak directivity, and is more of theoretical importance.

Derivation of antenna aperture from thermodynamic considerations

Diagram of antenna A and resistor R in thermal cavities, connected by filter F_ν. If both cavities are at the same temperature [math]\displaystyle{ T }[/math], [math]\displaystyle{ P_\text{A} = P_\text{R} }[/math]

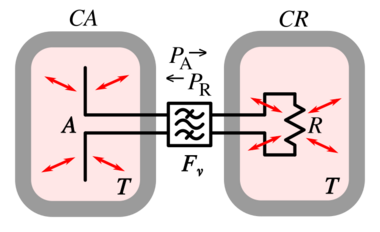
The aperture of an isotropic antenna, the basis of the definition of gain above, can be derived on the basis of consistency with thermodynamics. Suppose an ideal isotropic antenna A with a driving point impedance of R sits within a closed system (CA) in thermodynamic equilibrium at temperature T. We connect the antenna terminals to a resistor also of resistance R inside a second closed system (CR) also at temperature T. In between, an arbitrary lossless electronic filter F_ν may be inserted which only passes some frequency components.

Each cavity is in thermal equilibrium and thus filled with blackbody radiation due to temperature T. The resistor, due to that temperature, will generate an open-circuit voltage due to Johnson–Nyquist noise whose mean-squared spectral density is given by

[math]\displaystyle{ \overline {v_{n}^2} = 4 k_\text{B} T R \, \eta(f) }[/math]

where [math]\displaystyle{ \eta(f) }[/math] is a quantum mechanical factor applying to frequency f; at normal temperatures and electronic frequencies [math]\displaystyle{ \eta(f)=1 }[/math] but in general is given by

[math]\displaystyle{ \eta(f) = \frac{hf/k_\text{B} T}{e^{hf/k_\text{B} T} - 1} }[/math] .

The amount of power supplied by an electrical source of impedance R into a matched load (that is, something with an impedance of R, such as the antenna in CA) whose rms open circuit voltage is v_rms is given by

[math]\displaystyle{ P = \frac{\text{v}_\text{rms}^2}{4\text{R}} }[/math]

The mean-squared voltage [math]\displaystyle{ \overline {v_{n}^2} = \text{v}_\text{rms}^2 }[/math] can be found by integrating the above equation for the spectral density of mean-squared noise voltage over frequencies passed by the filter F_ν. For simplicity, let us just consider F_ν as a narrowband filter of bandwidth B₁ around center frequency f₁ in which case that integral simplifies as follows:

[math]\displaystyle{ P_R = \frac {\int_{0}^{\infty} 4 k_\text{B} T R \, \eta(f) \, F_\nu(f) \, df} {4\text{R}} }[/math]

[math]\displaystyle{ = \frac {4 k_\text{B} T R \, \eta(f_1) \, B_1} {4\text{R}} = k_\text{B} T \, \eta(f_1) \, B_1 }[/math]

This power due to Johnson noise from the resistor is received by the antenna which radiates it into the closed system CA.

The same antenna, being bathed in black-body radiation of temperature T, receives a spectral radiance (power per unit area per unit frequency per unit solid angle) given by Planck's law:

[math]\displaystyle{ \text{P}_{\text{f,A},\Omega}(f) = \frac{ 2 h f^3}{c^2} \frac{1}{e^{hf / k_\mathrm B \text{T}} - 1} = \frac{ 2 f^2}{c^2} \, k_\mathrm{B} \, \text{T} \, \eta(f) }[/math]

using the notation [math]\displaystyle{ \eta(f) }[/math] defined above.

However that radiation is unpolarized, whereas the antenna is only sensitive to one polarization, reducing it by a factor of 1/2. To find the total power from black-body radiation accepted by the antenna, we must integrate that quantity times the assumed cross-sectional area of the antenna A_eff over all solid angle Ω and over all frequency f:

[math]\displaystyle{ P_A = \int_{0}^{\infty} df \int_{4\pi} d\Omega \; \frac{ \text{P}_{\text{f,A},\Omega}(f)}{2} \text{A}_\text{eff}(\Omega, f) \, \text{F}_\nu(f) }[/math]

Since we have assumed an isotropic radiator, A_eff is independent of angle so the integration over solid angle is trivial, introducing a factor of 4π. And again we can take the simple case of a narrowband electronic filter function F_ν which only passes power of bandwidth B₁ around frequency f₁. The double integral then simplifies to:

[math]\displaystyle{ P_A = 2\pi \text{P}_{\text{f,A},\Omega}(f) \text{A}_\text{eff} \, B_1 = \frac{ 4\pi \, k_\mathrm{B} \, \text{T} \, \eta(f_1)} {\lambda_1^2} \text{A}_\text{eff} B_1 }[/math]

where [math]\displaystyle{ \lambda_1 = c/f_1 }[/math] is the free space wavelength corresponding to the frequency f₁.

Since each system is in thermodynamic equilibrium at the same temperature, we expect no net transfer of power between the cavities. Otherwise one cavity would heat up and the other would cool down in violation of the second law of thermodynamics. Therefore, the power flows in both directions must be equal

[math]\displaystyle{ P_A = P_R }[/math]

We can then solve for A_eff, the cross sectional area intercepted by the isotropic antenna:

[math]\displaystyle{ \frac{4 \pi \, k_\mathrm{B} \, \text{T} \, \eta(f_1)} {\lambda_1^2} \text{A}_\text{eff} B_1 = k_\text{B} T \, \eta(f_1) \, B_1 }[/math]

[math]\displaystyle{ \text{A}_\text{eff} = \frac {\lambda_1^2}{4\pi} }[/math]

We thus find that for a hypothetical isotropic antenna, thermodynamics demands that the effective cross-section of the receiving antenna to have an area of λ²/4π. This result could be further generalized if we allow the integral over frequency to be more general. Then we find that A_eff for the same antenna must vary with frequency according to that same formula, using λ=c/f. Moreover, the integral over solid angle can be generalized for an antenna that is not isotropic (that is, any real antenna!). Since the angle of arriving electromagnetic radiation only enters into A_eff in the above integral, we arrive at the simple but powerful result that the average of the effective cross section A_eff over all angles at wavelength λ must also be given by

[math]\displaystyle{ \overline{\text{A}_\text{eff}} = \frac {\lambda^2}{4\pi} \; }[/math] .

.

Although the above is sufficient proof, we can note that the condition of the antenna's impedance being R, the same as the resistor, can also be relaxed. In principle any antenna impedance (that isn't totally reactive) can be impedance matched to the resistor R by inserting a suitable (lossless) matching network. Since that network is lossless, the powers P_A and P_R will still flow in opposite directions, even though the voltage and currents seen at the antenna and resistor's terminals will differ. The spectral density of the power flow in either direction will still be given by [math]\displaystyle{ k_\text{B} T \, \eta(f) }[/math], and in fact this is the very thermal noise power spectral density associated with one electromagnetic mode, be it in free-space or transmitted electrically. Since there is only a single connection to the resistor, the resistor itself represents a single mode. And an antenna, also having a single electrical connection, couples to one mode of the electromagnetic field according to its average effective cross section of [math]\displaystyle{ \frac {\lambda_1^2}{4\pi} }[/math].

Notes

de:Apertur