Engineering:Stress intensity factor

Short description: Quantity in fracture mechanics; predicts stress intensity near a crack's tip

Polar coordinates at the crack tip.

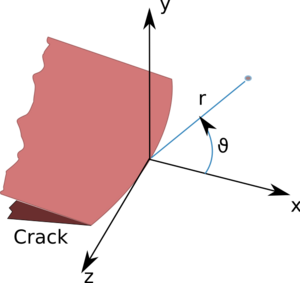
In fracture mechanics, the stress intensity factor (K) is used to predict the stress state ("stress intensity") near the tip of a crack or notch caused by a remote load or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic material and is useful for providing a failure criterion for brittle materials, and is a critical technique in the discipline of damage tolerance. The concept can also be applied to materials that exhibit small-scale yielding at a crack tip.

The magnitude of K depends on specimen geometry, the size and location of the crack or notch, and the magnitude and the distribution of loads on the material. It can be written as:

[math]\displaystyle{ K = \sigma \sqrt{\pi a} \, f(a/W) }[/math]

where [math]\displaystyle{ f(a/W) }[/math] is a specimen geometry dependent function of the crack length, a, and the specimen width, W, and σ is the applied stress.

Linear elastic theory predicts that the stress distribution ([math]\displaystyle{ \sigma_{ij} }[/math]) near the crack tip, in polar coordinates ([math]\displaystyle{ r,\theta }[/math]) with origin at the crack tip, has the form

[math]\displaystyle{ \sigma_{ij}(r, \theta) = \frac {K} {\sqrt{2 \pi r}}\,f_{ij} ( \theta) + \,\,\rm{higher\, order\, terms} }[/math]

where K is the stress intensity factor (with units of stress × length^1/2) and [math]\displaystyle{ f_{ij} }[/math] is a dimensionless quantity that varies with the load and geometry. Theoretically, as r goes to 0, the stress [math]\displaystyle{ \sigma_{ij} }[/math] goes to [math]\displaystyle{ \infty }[/math] resulting in a stress singularity. Practically however, this relation breaks down very close to the tip (small r) because plasticity typically occurs at stresses exceeding the material's yield strength and the linear elastic solution is no longer applicable. Nonetheless, if the crack-tip plastic zone is small in comparison to the crack length, the asymptotic stress distribution near the crack tip is still applicable.

Stress intensity factors for various modes

Mode I, Mode II, and Mode III crack loading.

In 1957, G. Irwin found that the stresses around a crack could be expressed in terms of a scaling factor called the stress intensity factor. He found that a crack subjected to any arbitrary loading could be resolved into three types of linearly independent cracking modes. These load types are categorized as Mode I, II, or III as shown in the figure. Mode I is an opening (tensile) mode where the crack surfaces move directly apart. Mode II is a sliding (in-plane shear) mode where the crack surfaces slide over one another in a direction perpendicular to the leading edge of the crack. Mode III is a tearing (antiplane shear) mode where the crack surfaces move relative to one another and parallel to the leading edge of the crack. Mode I is the most common load type encountered in engineering design.

Different subscripts are used to designate the stress intensity factor for the three different modes. The stress intensity factor for mode I is designated [math]\displaystyle{ K_{\rm I} }[/math] and applied to the crack opening mode. The mode II stress intensity factor, [math]\displaystyle{ K_{\rm II} }[/math], applies to the crack sliding mode and the mode III stress intensity factor, [math]\displaystyle{ K_{\rm III} }[/math], applies to the tearing mode. These factors are formally defined as:

[math]\displaystyle{ \begin{align} K_{\rm I} & = \lim_{r\rightarrow 0} \sqrt{2\pi r}\,\sigma_{yy}(r,0) \\ K_{\rm II} & = \lim_{r\rightarrow 0} \sqrt{2\pi r}\,\sigma_{yx}(r,0) \\ K_{\rm III} & = \lim_{r\rightarrow 0} \sqrt{2\pi r}\,\sigma_{yz}(r,0) \,. \end{align} }[/math]

Equations for stress and displacement fields

The mode I stress field expressed in terms of [math]\displaystyle{ K_{\rm I} }[/math] is [math]\displaystyle{ \left\{ \begin{align} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{xy} \end{align} \right\} = \frac{K_{\rm I}}{\sqrt{2\pi r}} \cos\frac{\theta}{2} \left\{ \begin{align} 1 - \sin\frac{\theta}{2}\sin\frac{3\theta}{2} \\ 1 + \sin\frac{\theta}{2}\sin\frac{3\theta}{2} \\ \sin\frac{\theta}{2}\cos\frac{3\theta}{2} \end{align} \right\} }[/math], and [math]\displaystyle{ \left\{ \begin{align} \sigma_{rr} \\ \sigma_{\theta \theta} \\ \sigma_{r \theta} \end{align} \right\} = \frac{K_{\rm I}}{\sqrt{2\pi r}} \cos\frac{\theta}{2} \left\{ \begin{align} 1 + \sin^2\frac{\theta}{2} \\ \cos^2\frac{\theta}{2} \\ \sin\frac{\theta}{2}\cos\frac{\theta}{2} \end{align} \right\} }[/math]. [math]\displaystyle{ \sigma_{zz} = \nu_1 (\sigma_{xx} + \sigma_{yy}) = \nu_1 (\sigma_{rr} + \sigma_{\theta\theta}) }[/math], [math]\displaystyle{ \sigma_{xz} = \sigma_{yz} = \sigma_{rz} = \sigma_{\theta z} = 0 }[/math]. The displacements are [math]\displaystyle{ \left\{ \begin{align} u_x \\ u_y \end{align} \right\} = \frac{K_{\rm I}}{2E} \sqrt{\frac{r}{2\pi}} \left\{ \begin{align} (1+ \nu) \left[ (2\kappa - 1) \cos\frac{\theta}{2} - \cos\frac{3\theta}{2} \right] \\ (1+ \nu) \left[ (2\kappa + 1) \sin\frac{\theta}{2} - \sin\frac{3\theta}{2} \right] \end{align} \right\} }[/math] [math]\displaystyle{ \left\{ \begin{align} u_r \\ u_\theta \end{align} \right\} = \frac{K_{\rm I}}{2E} \sqrt{\frac{r}{2\pi}} \left\{ \begin{align} (1+ \nu) \left[ (2\kappa - 1) \cos\frac{\theta}{2} - \cos\frac{3\theta}{2} \right] \\ (1+ \nu) \left[ -(2\kappa - 1) \sin\frac{\theta}{2} + \sin\frac{3\theta}{2} \right] \end{align} \right\} }[/math] [math]\displaystyle{ u_z = -\left(\frac{\nu_2 z}{E}\right) (\sigma_{xx} + \sigma_{yy}) = -\left(\frac{\nu_2 z}{E}\right) (\sigma_{rr} + \sigma_{\theta\theta}) }[/math] Where, for plane stress conditions [math]\displaystyle{ \kappa = \frac{(3 - \nu) }{(1 + \nu)} }[/math], [math]\displaystyle{ \nu_1 = 0 }[/math], [math]\displaystyle{ \nu_2=\nu }[/math], and for plane strain [math]\displaystyle{ \kappa = (3 - 4 \nu) }[/math], [math]\displaystyle{ \nu_1 = \nu }[/math], [math]\displaystyle{ \nu_2 = 0 }[/math]. For mode II [math]\displaystyle{ \left\{ \begin{align} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{xy} \end{align} \right\} = \frac{K_{\rm II}}{\sqrt{2\pi r}} \left\{ \begin{align} - \sin\frac{\theta}{2}(2+\cos\frac{\theta}{2}\cos\frac{3\theta}{2} ) \\ \sin\frac{\theta}{2}\cos\frac{\theta}{2} \sin\frac{3\theta}{2} \\ \cos\frac{\theta}{2} (1-\sin\frac{\theta}{2}\sin\frac{3\theta}{2}) \end{align} \right\} }[/math] and [math]\displaystyle{ \left\{ \begin{align} \sigma_{rr} \\ \sigma_{\theta\theta} \\ \sigma_{r\theta} \end{align} \right\} = \frac{K_{\rm II}}{\sqrt{2\pi r}} \left\{ \begin{align} \sin\frac{\theta}{2}(1-3\sin^2\frac{\theta}{2}) \\ -3 \sin\frac{\theta}{2}\cos^2\frac{\theta}{2} \\ \cos\frac{\theta}{2} (1-3\sin^2\frac{\theta}{2}) \end{align} \right\} }[/math], [math]\displaystyle{ \sigma_{zz} = \nu_1(\sigma_{xx} + \sigma_{yy}) = \nu_1 (\sigma_{rr} + \sigma_{\theta\theta}) }[/math], [math]\displaystyle{ \sigma_{xz} = \sigma_{yz} = \sigma_{rz} = \sigma_{\theta z} = 0 }[/math]. [math]\displaystyle{ \left\{ \begin{align} u_x \\ u_y \end{align} \right\} = \frac{K_{\rm II}}{2E} \sqrt{\frac{r}{2\pi}} \left\{ \begin{align} (1+ \nu) \left[ (2\kappa + 3) \sin\frac{\theta}{2} + \sin\frac{3\theta}{2} \right] \\ -(1+ \nu) \left[ (2\kappa - 3) \cos\frac{\theta}{2} + \cos\frac{3\theta}{2} \right] \end{align} \right\} }[/math] [math]\displaystyle{ \left\{ \begin{align} u_r \\ u_\theta \end{align} \right\} = \frac{K_{\rm II}}{2E} \sqrt{\frac{r}{2\pi}} \left\{ \begin{align} (1+ \nu) \left[ -(2\kappa - 1) \sin\frac{\theta}{2} + 3\sin\frac{3\theta}{2} \right] \\ (1+ \nu) \left[ -(2\kappa + 1) \cos\frac{\theta}{2} + 3\cos\frac{3\theta}{2} \right] \end{align} \right\} }[/math] [math]\displaystyle{ u_z = -\left(\frac{\nu_2 z}{E} \right) (\sigma_{xx} + \sigma_{yy}) = -\left(\frac{\nu_2 z}{E}\right)(\sigma_{rr} + \sigma_{\theta\theta}) }[/math] And finally, for mode III [math]\displaystyle{ \left\{ \begin{align} \sigma_{xz} \\ \sigma_{yz} \end{align} \right\} = \frac{K_{\rm III}}{\sqrt{2\pi r}} \left\{ \begin{align} -\sin\frac{\theta}{2} \\ \cos\frac{\theta}{2} \end{align} \right\} }[/math] [math]\displaystyle{ \left\{ \begin{align} \sigma_{rz} \\ \sigma_{\theta z} \end{align} \right\} = \frac{K_{\rm III}}{\sqrt{2\pi r}} \left\{ \begin{align} \sin\frac{\theta}{2} \\ \cos\frac{\theta}{2} \end{align} \right\} }[/math] with [math]\displaystyle{ \sigma_{xx} = \sigma_{yy} = \sigma_{rr} = \sigma_{\theta\theta} = \sigma_{zz} = \sigma_{xy} = \sigma_{r\theta} = 0 }[/math]. [math]\displaystyle{ u_z = \frac{2K_{\rm III}}{E} \sqrt{\frac{r}{2\pi}} \left\{ 2(1+\nu) \sin \frac{\theta}{2} \right\} }[/math], [math]\displaystyle{ u_x = u_y = u_r = u_\theta = 0 }[/math].

Relationship to energy release rate and J-integral

In plane stress conditions, the strain energy release rate ([math]\displaystyle{ G }[/math]) for a crack under pure mode I, or pure mode II loading is related to the stress intensity factor by:

[math]\displaystyle{ G_{\rm I} = K_{\rm I}^2\left(\frac{1}{E}\right) }[/math]

[math]\displaystyle{ G_{\rm II} = K_{\rm II}^2\left(\frac{1}{E}\right) }[/math]

where [math]\displaystyle{ E }[/math] is the Young's modulus and [math]\displaystyle{ \nu }[/math] is the Poisson's ratio of the material. The material is assumed to be an isotropic, homogeneous, and linear elastic. The crack has been assumed to extend along the direction of the initial crack

For plane strain conditions, the equivalent relation is a little more complicated:

[math]\displaystyle{ G_{\rm I} = K_{\rm I}^2\left(\frac{1-\nu^2}{E}\right)\, }[/math]

[math]\displaystyle{ G_{\rm II} = K_{\rm II}^2\left(\frac{1-\nu^2}{E}\right)\,. }[/math]

For pure mode III loading,

[math]\displaystyle{ G_{\rm III} = K_{\rm III}^2\left(\frac{1}{2\mu}\right) = K_{\rm III}^2\left(\frac{1+\nu}{E}\right) }[/math]

where [math]\displaystyle{ \mu }[/math] is the shear modulus. For general loading in plane strain, the linear combination holds:

[math]\displaystyle{ G = G_{\rm I} + G_{\rm II} + G_{\rm III}\,. }[/math]

A similar relation is obtained for plane stress by adding the contributions for the three modes.

The above relations can also be used to connect the J-integral to the stress intensity factor because

[math]\displaystyle{ G = J = \int_\Gamma \left(W~dx_2 - \mathbf{t}\cdot\cfrac{\partial\mathbf{u}}{\partial x_1}~ds\right) \,. }[/math]

Critical stress intensity factor

The stress intensity factor, [math]\displaystyle{ K }[/math], is a parameter that amplifies the magnitude of the applied stress that includes the geometrical parameter [math]\displaystyle{ Y }[/math] (load type). Stress intensity in any mode situation is directly proportional to the applied load on the material. If a very sharp crack, or a V-notch can be made in a material, the minimum value of [math]\displaystyle{ K_\mathrm{I} }[/math] can be empirically determined, which is the critical value of stress intensity required to propagate the crack. This critical value determined for mode I loading in plane strain is referred to as the critical fracture toughness ([math]\displaystyle{ K_\mathrm{Ic} }[/math]) of the material. [math]\displaystyle{ K_\mathrm{Ic} }[/math] has units of stress times the root of a distance (e.g. MN/m^3/2). The units of [math]\displaystyle{ K_\mathrm{Ic} }[/math] imply that the fracture stress of the material must be reached over some critical distance in order for [math]\displaystyle{ K_\mathrm{Ic} }[/math] to be reached and crack propagation to occur. The Mode I critical stress intensity factor, [math]\displaystyle{ K_\mathrm{Ic} }[/math], is the most often used engineering design parameter in fracture mechanics and hence must be understood if we are to design fracture tolerant materials used in bridges, buildings, aircraft, or even bells.

Polishing cannot detect a crack. Typically, if a crack can be seen it is very close to the critical stress state predicted by the stress intensity factor.

G–criterion

The G-criterion is a fracture criterion that relates the critical stress intensity factor (or fracture toughness) to the stress intensity factors for the three modes. This failure criterion is written as

[math]\displaystyle{ K_{\rm c}^2 = K_{\rm I}^2 + K_{\rm II}^2 + \frac{E'}{2\mu}\,K_{\rm III}^2 }[/math]

where [math]\displaystyle{ K_{\rm c} }[/math] is the fracture toughness, [math]\displaystyle{ E' = E/(1-\nu^2) }[/math] for plane strain and [math]\displaystyle{ E' = E }[/math] for plane stress. The critical stress intensity factor for plane stress is often written as [math]\displaystyle{ K_{\rm c} }[/math].

Examples

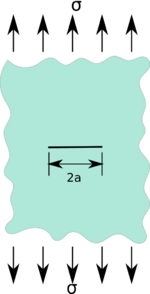
Infinite plate: Uniform uniaxial stress

The stress intensity factor for an assumed straight crack of length [math]\displaystyle{ 2a }[/math] perpendicular to the loading direction, in an infinite plane, having a uniform stress field [math]\displaystyle{ \sigma }[/math] is [math]\displaystyle{ K_\mathrm{I}=\sigma \sqrt{\pi a} }[/math]

Crack in an infinite plate under mode I loading.

Penny-shaped crack in an infinite domain

The stress intensity factor at the tip of a penny-shaped crack of radius [math]\displaystyle{ a }[/math] in an infinite domain under uniaxial tension [math]\displaystyle{ \sigma }[/math] is [math]\displaystyle{ K_{\rm I} = \frac{2}{\pi}\sigma\sqrt{\pi a} \,. }[/math]

Penny-shaped crack in an infinite domain under uniaxial tension.

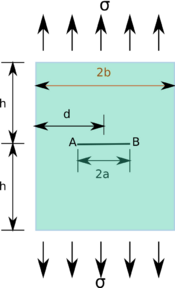
Finite plate: Uniform uniaxial stress

If the crack is located centrally in a finite plate of width [math]\displaystyle{ 2b }[/math] and height [math]\displaystyle{ 2h }[/math], an approximate relation for the stress intensity factor is [math]\displaystyle{ K_{\rm I} = \sigma \sqrt{\pi a}\left[\cfrac{1 - \frac{a}{2b} + 0.326\left(\frac{a}{b}\right)^2}{\sqrt{1 - \frac{a}{b}}}\right] \,. }[/math] If the crack is not located centrally along the width, i.e., [math]\displaystyle{ d \ne b }[/math], the stress intensity factor at location A can be approximated by the series expansion [math]\displaystyle{ K_{\rm IA} = \sigma \sqrt{\pi a}\left[1 + \sum_{n=2}^{M} C_n\left(\frac{a}{b}\right)^n\right] }[/math] where the factors [math]\displaystyle{ C_n }[/math] can be found from fits to stress intensity curves for various values of [math]\displaystyle{ d }[/math]. A similar (but not identical) expression can be found for tip B of the crack. Alternative expressions for the stress intensity factors at A and B are [math]\displaystyle{ K_{\rm IA} = \sigma\sqrt{\pi a}\,\Phi_A \,\, , K_{\rm IB} = \sigma\sqrt{\pi a}\,\Phi_B }[/math] where [math]\displaystyle{ \begin{align} \Phi_A &:= \left[\beta + \left(\frac{1-\beta}{4}\right)\left(1 + \frac{1}{4\sqrt{\sec\alpha_A}}\right)^2\right]\sqrt{\sec\alpha_A} \\ \Phi_B &:= 1 + \left[\frac{\sqrt{\sec\alpha_{AB}} - 1}{1 + 0.21\sin\left\{8\,\tan^{-1}\left[\left(\frac{\alpha_A - \alpha_B}{\alpha_A + \alpha_B}\right)^{0.9}\right]\right\}}\right] \end{align} }[/math] with [math]\displaystyle{ \beta := \sin\left(\frac{\pi\alpha_B}{\alpha_A+\alpha_B}\right) ~,~~ \alpha_A := \frac{\pi a}{2 d} ~,~~ \alpha_B := \frac{\pi a}{4b - 2d} ~;~~ \alpha_{AB} := \frac{4}{7}\,\alpha_A + \frac{3}{7}\,\alpha_B \,. }[/math] In the above expressions [math]\displaystyle{ d }[/math] is the distance from the center of the crack to the boundary closest to point A. Note that when [math]\displaystyle{ d=b }[/math] the above expressions do not simplify into the approximate expression for a centered crack.

Crack in a finite plate under mode I loading.

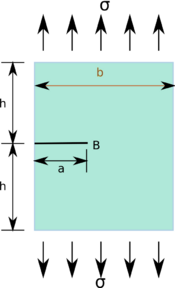
Edge crack in a plate under uniaxial stress

For a plate having dimensions [math]\displaystyle{ 2h \times b }[/math] containing an unconstrained edge crack of length [math]\displaystyle{ a }[/math], if the dimensions of the plate are such that [math]\displaystyle{ h/b \ge 0.5 }[/math] and [math]\displaystyle{ a/b \le 0.6 }[/math], the stress intensity factor at the crack tip under a uniaxial stress [math]\displaystyle{ \sigma }[/math] is [math]\displaystyle{ K_{\rm I} = \sigma\sqrt{\pi a}\left[1.122 - 0.231\left(\frac{a}{b}\right) + 10.55\left(\frac{a}{b}\right)^2 - 21.71\left(\frac{a}{b}\right)^3 + 30.382\left(\frac{a}{b}\right)^4\right] \,. }[/math] For the situation where [math]\displaystyle{ h/b \ge 1 }[/math] and [math]\displaystyle{ a/b \ge 0.3 }[/math], the stress intensity factor can be approximated by [math]\displaystyle{ K_{\rm I} = \sigma\sqrt{\pi a}\left[\frac{1 + 3\frac{a}{b}}{2\sqrt{\pi\frac{a}{b}}\left(1-\frac{a}{b}\right)^{3/2}}\right] \,. }[/math]

Edge crack in a finite plate under uniaxial stress.

Infinite plate: Slanted crack in a biaxial stress field

For a slanted crack of length [math]\displaystyle{ 2a }[/math] in a biaxial stress field with stress [math]\displaystyle{ \sigma }[/math] in the [math]\displaystyle{ y }[/math]-direction and [math]\displaystyle{ \alpha\sigma }[/math] in the [math]\displaystyle{ x }[/math]-direction, the stress intensity factors are [math]\displaystyle{ \begin{align} K_{\rm I} & = \sigma\sqrt{\pi a}\left(\cos^2\beta + \alpha \sin^2\beta\right) \\ K_{\rm II} & = \sigma\sqrt{\pi a}\left(1- \alpha\right)\sin\beta\cos\beta \end{align} }[/math] where [math]\displaystyle{ \beta }[/math] is the angle made by the crack with the [math]\displaystyle{ x }[/math]-axis.

A slanted crack in a thin plate under biaxial load.

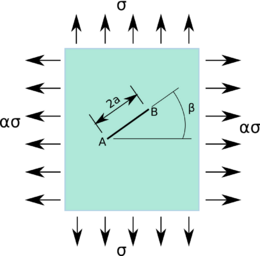Crack in a plate under point in-plane force

Consider a plate with dimensions [math]\displaystyle{ 2h \times 2b }[/math] containing a crack of length [math]\displaystyle{ 2a }[/math]. A point force with components [math]\displaystyle{ F_x }[/math] and [math]\displaystyle{ F_y }[/math] is applied at the point ([math]\displaystyle{ x,y }[/math]) of the plate. For the situation where the plate is large compared to the size of the crack and the location of the force is relatively close to the crack, i.e., [math]\displaystyle{ h \gg a }[/math], [math]\displaystyle{ b \gg a }[/math], [math]\displaystyle{ x \ll b }[/math], [math]\displaystyle{ y \ll h }[/math], the plate can be considered infinite. In that case, for the stress intensity factors for [math]\displaystyle{ F_x }[/math] at crack tip B ([math]\displaystyle{ x = a }[/math]) are [math]\displaystyle{ \begin{align} K_{\rm I} & = \frac{F_x}{2\sqrt{\pi a}}\left(\frac{\kappa -1}{\kappa+1}\right) \left[G_1 + \frac{1}{\kappa-1} H_1\right] \\ K_{\rm II} & = \frac{F_x}{2\sqrt{\pi a}} \left[G_2 + \frac{1}{\kappa+1} H_2\right] \end{align} }[/math] where [math]\displaystyle{ \begin{align} G_1 & = 1 - \text{Re}\left[\frac{a+z}{\sqrt{z^2-a^2}}\right] \,,\,\, G_2 = - \text{Im}\left[\frac{a+z}{\sqrt{z^2-a^2}}\right] \\ H_1 & = \text{Re}\left[\frac{a(\bar{z}-z)}{(\bar{z}-a)\sqrt{{\bar{z}}^2-a^2}}\right] \,,\,\, H_2 = -\text{Im}\left[\frac{a(\bar{z}-z)}{(\bar{z}-a)\sqrt{{\bar{z}}^2-a^2}}\right] \end{align} }[/math] with [math]\displaystyle{ z = x + iy }[/math], [math]\displaystyle{ \bar{z} = x - iy }[/math], [math]\displaystyle{ \kappa = 3-4\nu }[/math] for plane strain, [math]\displaystyle{ \kappa= (3-\nu)/(1+\nu) }[/math] for plane stress, and [math]\displaystyle{ \nu }[/math] is the Poisson's ratio. The stress intensity factors for [math]\displaystyle{ F_y }[/math] at tip B are [math]\displaystyle{ \begin{align} K_{\rm I} & = \frac{F_y}{2\sqrt{\pi a}} \left[G_2 - \frac{1}{\kappa+1} H_2\right] \\ K_{\rm II} & = -\frac{F_y}{2\sqrt{\pi a}}\left(\frac{\kappa -1}{\kappa+1}\right) \left[G_1 - \frac{1}{\kappa-1} H_1\right] \,. \end{align} }[/math] The stress intensity factors at the tip A ([math]\displaystyle{ x = -a }[/math]) can be determined from the above relations. For the load [math]\displaystyle{ F_x }[/math] at location [math]\displaystyle{ (x,y) }[/math], [math]\displaystyle{ K_{\rm I}(-a; x,y) = -K_{\rm I}(a; -x,y) \,,\,\, K_{\rm II}(-a; x,y) = K_{\rm II}(a; -x,y) \,. }[/math] Similarly for the load [math]\displaystyle{ F_y }[/math], [math]\displaystyle{ K_{\rm I}(-a; x,y) = K_{\rm I}(a; -x,y) \,,\,\, K_{\rm II}(-a; x,y) = -K_{\rm II}(a; -x,y) \,. }[/math]

A crack in a plate under the action of a localized force with components [math]\displaystyle{ F_x }[/math] and [math]\displaystyle{ F_y }[/math].

Loaded crack in a plate

If the crack is loaded by a point force [math]\displaystyle{ F_y }[/math] located at [math]\displaystyle{ y=0 }[/math] and [math]\displaystyle{ -a \lt x \lt a }[/math], the stress intensity factors at point B are [math]\displaystyle{ K_{\rm I} = \frac{F_y}{2\sqrt{\pi a}}\sqrt{\frac{a+x}{a-x}}\,,\,\, K_{\rm II} = -\frac{F_x}{2\sqrt{\pi a}}\left(\frac{\kappa -1}{\kappa+1}\right) \,. }[/math] If the force is distributed uniformly between [math]\displaystyle{ -a \lt x \lt a }[/math], then the stress intensity factor at tip B is [math]\displaystyle{ K_{\rm I} = \frac{1}{2\sqrt{\pi a}}\int_{-a}^a F_y(x)\,\sqrt{\frac{a+x}{a-x}}\,{\rm d}x\,,\,\, K_{\rm II} = -\frac{1}{2\sqrt{\pi a}}\left(\frac{\kappa -1}{\kappa+1}\right)\int_{-a}^a F_y(x)\,{\rm d}x, \,. }[/math]

A loaded crack in a plate.

Stack of Parallel Cracks in an Infinite Plate

If the crack spacing is much greater than the crack length (h >> a), the interaction effect between neighboring cracks can be ignored, and the stress intensity factor is equal to that of a single crack of length 2a.

Then the stress intensity factor at crack tip is

[math]\displaystyle{ \begin{align} K_{\rm I} & = \sigma\sqrt{\pi a} \end{align} }[/math]

If the crack length is much greater than the spacing (a >> h ), the cracks can be considered as a stack of semi-infinite cracks.

Then the stress intensity factor at crack tip is

[math]\displaystyle{ \begin{align} K_{\rm I} & = \sigma\sqrt{h} \end{align} }[/math]

Compact tension specimen

The stress intensity factor at the crack tip of a compact tension specimen is [math]\displaystyle{ \begin{align} K_{\rm I} & = \frac{P}{B}\sqrt{\frac{\pi}{W}}\left[16.7\left(\frac{a}{W}\right)^{1/2} - 104.7\left(\frac{a}{W}\right)^{3/2} + 369.9\left(\frac{a}{W}\right)^{5/2} \right.\\ & \qquad \left.- 573.8\left(\frac{a}{W}\right)^{7/2} + 360.5\left(\frac{a}{W}\right)^{9/2} \right] \end{align} }[/math] where [math]\displaystyle{ P }[/math] is the applied load, [math]\displaystyle{ B }[/math] is the thickness of the specimen, [math]\displaystyle{ a }[/math] is the crack length, and [math]\displaystyle{ W }[/math] is the width of the specimen.

Compact tension specimen for fracture toughness testing.

Single-edge notch-bending specimen

The stress intensity factor at the crack tip of a single-edge notch-bending specimen is [math]\displaystyle{ \begin{align} K_{\rm I} & = \frac{4P}{B}\sqrt{\frac{\pi}{W}}\left[1.6\left(\frac{a}{W}\right)^{1/2} - 2.6\left(\frac{a}{W}\right)^{3/2} + 12.3\left(\frac{a}{W}\right)^{5/2} \right.\\ & \qquad \left.- 21.2\left(\frac{a}{W}\right)^{7/2} + 21.8\left(\frac{a}{W}\right)^{9/2} \right] \end{align} }[/math] where [math]\displaystyle{ P }[/math] is the applied load, [math]\displaystyle{ B }[/math] is the thickness of the specimen, [math]\displaystyle{ a }[/math] is the crack length, and [math]\displaystyle{ W }[/math] is the width of the specimen.

Single-edge notch-bending specimen (also called three-point bending specimen) for fracture toughness testing

See also

• Fracture mechanics
• Fracture toughness
• Strain energy release rate
• J-integral
• Material failure theory
• Paris' law

External links

• Kathiresan, K. ; Hsu, T. M. ; Brussat, T. R., 1984, Advanced Life Analysis Methods. Volume 2. Crack Growth Analysis Methods for Attachment Lugs
• Stress Intensity Factor on www.fracturemechanics.org, by Bob McGinty