Engineering:Substrate inhibition in bioreactors

Substrate inhibition in bioreactors occurs when the concentration of substrate (such as glucose, salts, or phenols) exceeds the optimal parameters and reduces the growth rate of the cells within the bioreactor. This is often confused with substrate limitation, which describes environments in which cell growth is limited due to of low substrate. Limited conditions can be modeled with the Monod equation; however, the Monod equation is no longer suitable in substrate inhibiting conditions. A Monod deviation, such as the Haldane (Andrew) equation, is more suitable for substrate inhibiting conditions. These cell growth models are analogous to equations that describe enzyme kinetics, although, unlike enzyme kinetics parameters, cell growth parameters are generally empirically estimated.

General Principles

Cell growth in bioreactors depends on a wide range of environmental and physiological conditions such as substrate concentration. With regards to bioreactor cell growth, substrate refers to the nutrients that the cells consume and is contained within the bioreactor medium. Cell growth can either be substrate limited or inhibited depending on whether the substrate concentration is too low or too high, respectively. The Monod equation accurately describes limiting conditions, but substrate inhibition models are more complex.

Substrate inhibition occurs when the rate of microbial growth lessens due to a high concentration of substrate. Higher substrate concentrations are usually caused by osmotic issues, viscosity, or inefficient oxygen transport. By slowly adding substrate into the medium, fed-batch bioreactor systems can help alleviate substrate inhibition. Substrate inhibition is also closely related to enzyme kinetics which is commonly modeled by the Michaelis–Menten equation. If an enzyme that is part of a rate-limiting step of microbial growth is substrate inhibited, then the cell growth will be inhibited in the same manner. However, the mechanisms are often more complex, and parameters for a model equation need to be estimated from experimental data. Additionally, information on inhibitory effects caused by mixtures of compounds is limited because most studies have been performed with single-substrate systems

Types of Inhibition

Enzyme Kinetics Overview

This plot depicts the reaction velocity versus substrate concentration, modeled by the Michaelis-Menten equation for competitive inhibition (dotted black) and non-competitive inhibition (solid grey) compared to normal enzyme activity (solid black).

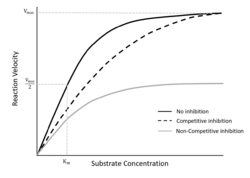
thumb|A plot depicting the initial reaction rate versus substrate concentration as modeled by the Michaelis-Menten equation (solid line) and the Haldane equation for substrate inhibition (dotted line).One of the most well known equations to describe single-substrate enzyme kinetics is the Michaelis-Menten equation. This equation relates the initial rate of reaction to the concentration of substrate present, and deviations of model can be used to predict competitive inhibition and non-competitive inhibition. The model takes the form of the following equation:

[math]\displaystyle{ \nu=\frac{V_m[S]}{K_M+[S]} }[/math] (Michaelis-Menten equation)

Where

[math]\displaystyle{ K_M }[/math] is the Michaelis constant

[math]\displaystyle{ \nu }[/math] is the initial reaction rate

[math]\displaystyle{ V_m }[/math] is the maximum reaction rate

If the inhibitor is different from the substrate, then competitive inhibition will increase Km while Vmax remains the same, and non-competitive will decrease Vmax while Km remains the same. However, under substrate inhibiting effects where two of the same substrate molecules bind to the active sites and inhibitory sites, the reaction rate will reach a peak value before decreasing. The reaction rate will either decrease to zero under complete inhibition, or it will decrease to a non-zero asymptote during partial inhibition. This can be described by the Haldane (or Andrew) equation, which is a common deviation of the Michaelis-Menten equation, and takes the following form:

[math]\displaystyle{ \nu=\frac{V_m[S]}{K_M+[S]+\frac{[S]^2}{K_I}} }[/math] (Haldane equation for single-substrate inhibition of enzymatic reaction rate)

Where

[math]\displaystyle{ K_I }[/math] is the inhibition constant

Cell Growth in Bioreactors

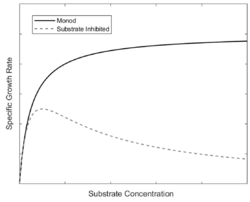
Bioreactor cell growth kinetics is analogous to the equations presented in enzyme kinetics. Under non-inhibiting single-substrate conditions, the specific growth rate of biomass can be modeled by the well-known Monod equation. The Monod equation models the growth of organisms during substrate limiting conditions, and its parameters are determined through experimental observation. The Monod equation is based on a single substrate-consuming enzyme system that follows the Michaelis-Menten equation. The Monod takes the following familiar form:

[math]\displaystyle{ \mu=\frac{\mu_m[S]}{K_S+[S]} }[/math] (Monod equation)

Where:

[math]\displaystyle{ K_S }[/math] is the saturation constant

[math]\displaystyle{ \mu }[/math] is the specific growth rate

[math]\displaystyle{ \mu_m }[/math] is the maximum specific growth rate

A plot depicting the specific growth rate versus substrate concentration as modeled by the Monod equation (solid line) and the Haldane equation for substrate inhibition (dotted line).

Under single-substrate inhibiting conditions, the Monod equation is no longer suitable, and the most common Monod derivative is once again in the form of the Haldane equation. As in enzyme kinetics, the growth rate will initially increase as substrate is increased before reaching a peak and decreasing at high substrate concentrations. Reasons for substrate inhibition in bioreactor cell growth includes osmotic issues, viscosity, or inefficient oxygen transport due to overly concentrated substrate in the bioreactor medium. Substrates that are known to cause inhibition include glucose, NaCl, and phenols, among others Substrate inhibition is also a concern in wastewater treatment, where one of the most studied biodegradation substrates are the toxic phenols. Due to their toxicity, there is a large interest in bioremediation of phenols, and it is well known that phenol inhibition can be modeled by the following Haldane equation:

[math]\displaystyle{ \mu=\frac{\mu_m[S]}{K_S+[S]+\frac{[S]^2}{K_I}} }[/math] (Haldane equation for single-substrate inhibition of cell growth)

Where:

[math]\displaystyle{ K_I }[/math] is the inhibition constant

There are several equations that have been developed to describe substrate inhibition. Two equations listed below that are referred to as non-competitive substrate inhibition and competitive substrate inhibition models respectively by Shuler and Michael in Bioprocess Engineering: Basic Concepts. Note that the Haldane equation above is a special case of the following non-competitive substrate inhibition model, where KI >>Ks.

[math]\displaystyle{ \mu=\frac{\mu_m}{(1+\frac{K_S}{[S]})(1+\frac{[S]}{K_I})} }[/math] (non-competitive single-substrate inhibition)

[math]\displaystyle{ \mu=\frac{\mu_m[S]}{K_S(1+\frac{[S]}{K_I})+[S]} }[/math] (competitive single-substrate inhibition)

These equations also have enzymatic counterparts, where the equations commonly describe the interactions between substrate and inhibitors at the active and inhibitory sites. The concept of competitive and non-competitive substrate inhibition is more well defined in enzyme kinetics, but these analogous equations also apply to cell growth models.

Overcoming Substrate Inhibition in Bioreactors

Substrate inhibition can be characterized by a high substrate concentration and decreased growth rate, resulting in decreased bioreactor outputs. The most common solution is to change the growth from a batch process to a fed-batch process. Other methods to overcome substrate inhibition include the addition of another substrate type in order to develop alternative metabolic pathways, immobilizing the cells or increasing the biomass concentration.

Utilizing Fed-Batch

A fed-batch process is the most common way to decrease the effects of substrate inhibition. Fed-batch processes are characterized by the continuous addition of bioreactor media (which includes the substrate) into the inoculum (cellular solution). The addition of media will increase the overall volume within the reactor along with substrate and other growth materials. A fed-batch process will also have an output flow rate of the substrate/cell/product mixture which can be collected to retrieve the desired product. Fed-batch is a good way to overcome substrate inhibition because the amount of substrate can be changed at various points in the growth process. This allows for the bioreactor technician to provide the cells with the amount of substrate they need rather than providing them too much or too little.

Other methods

Other methods to overcome substrate inhibition include the use of Two Phase Partitioning Bioreactors, the immobilization of cells, and increasing the biomass concentration in the bioreactor.

Two Phase Partitioning Bioreactors are able to reduce the aqueous phase substrate concentration by storing substrate in an alternative phase, which can be re-released into the biomass based on metabolic demand. The cell immobilization method the bioreactor works by encapsulating the cells into a material that makes the removal of inhibitory compounds easier, thus reducing inhibition by creating a matrix with the cells which can act as a protective barrier against the inhibitory effects of toxic materials. The method of increasing cell concentration is done by supporting the cellular material on a scaffold to create a biofilm. Biofilms allow for extremely high cell concentrations while preventing the overgrowth of inhibitory substrates.

Impact On Product Production

The impact of product production depends on how the product is created. Substrate inhibition will affect products produced by enzymatic reactions differently than growth associated product formation. Substrate inhibition of enzymatic product production will inhibit the enzyme's activity, which will lower the reaction rate and reduce the rate of product formation. However, if a product is being produced by cells, then substrate inhibition will narrow product formation by limiting the growth of cells.

Growth Associated Products

There are multiple relationships that may exist between the rate of product formation, the specific rate of substrate consumption, and specific growth rate. The following equations demonstrate the relationship between cell growth and product production for growth associated production. The parameters [math]\displaystyle{ q_p }[/math] and [math]\displaystyle{ \mu }[/math] (specific rate of product formation and specific growth rate respectively) are defined below.

[math]\displaystyle{ q_p = \frac{1}{X} \frac{dP}{dt} }[/math] (specific rate of product formation)

[math]\displaystyle{ \mu = \frac{1}{X}\frac{dX}{dt} }[/math] (specific growth rate)

Where [math]\displaystyle{ X }[/math] is the cell concentration, and [math]\displaystyle{ P }[/math] is the product concentration.

The product formation and cell growth are both directly linked to the amount of substrate consumed through the yield coefficients, [math]\displaystyle{ Y_{\frac{P}{S}} }[/math] and [math]\displaystyle{ Y_{\frac{X}{S}} }[/math]respectively. These coefficients can be combined to define a yield coefficient, [math]\displaystyle{ Y_{\frac{P}{X}} }[/math], that relates the product production to cell growth.

[math]\displaystyle{ \frac{Y_{\frac{P}{S}}}{Y_{\frac{X}{S}}}= Y_{\frac{P}{X}} = \frac{\Delta P}{\Delta X} }[/math]

This yield coefficient can be further used to directly relate the rate of change of product to the rate of change of cell growth

[math]\displaystyle{ \frac{dP}{dt} = Y_{\frac{P}{X}}\frac{dX}{dt} \rightarrow \frac{dP}{dt} = Y_{\frac{P}{X}}X\frac{1}{X}\frac{dX}{dt} }[/math]

Rearranging this equation gives the following relationship between the specific rate of product formation and the specific growth rate of the cells for growth associated products.

[math]\displaystyle{ q_P = Y_{\frac{P}{X}}\mu }[/math]

The above relationships demonstrate that for growth associated product, the specific growth rate is directly proportional to the specific rate of product formation. Furthermore, substrate inhibition limits the specific growth rate, which reduces the final biomass concentration. Increasing the substrate concentration may increase the viscosity of the media, lowers the rate of oxygen diffusivity, and affect the osmolarity of the system. These effects can be detrimental to cell growth, and by extension, the yield of product.