Engineering:Ward Leonard control

Ward Leonard control, also known as the Ward Leonard drive system, was a widely used DC motor speed control system introduced by Harry Ward Leonard in 1891. In the early 1900s, the control system of Ward Leonard was adopted by the U.S. Navy and also used in passenger lifts of large mines. It also provided a solution to a moving sidewalk at the Paris Exposition of 1900, where many others had failed to operate properly. It was applied to railway locomotives used in World War I, and was used in anti-aircraft radars in World War II. Connected to automatic anti-aircraft gun directors, the tracking motion in two dimensions had to be extremely smooth and precise. The MIT Radiation Laboratory selected Ward-Leonard to equip the famous radar SCR-584 in 1942. The Ward Leonard control system was widely used for elevators until thyristor drives became available in the 1980s, because it offered smooth speed control and consistent torque. Many Ward Leonard control systems and variations on them remain in use.

Basic concept

The key feature of the Ward Leonard control system is the ability to smoothly vary the speed of a DC motor, including reversing it, by controlling the field and hence the output voltage of a DC generator, as well as the field of the motor itself. As the speed of a DC motor is dictated by the supplied voltage, this gives simple speed control. The DC generator could be driven by any means. This 'prime mover' could be an AC motor, or it could be an internal combustion engine (its application to vehicles was patented by H.W. Leonard in 1903).

A Ward Leonard drive can be viewed as a high-power amplifier in the multi-kilowatt range, built from rotating electrical machinery. Where the 'prime mover' is electrical, a Ward Leonard drive unit consists of a motor and generator with shafts coupled together. The prime mover, which turns at a constant speed, may be AC or DC powered. The generator is a DC generator, with field windings and armature windings. The input to the amplifier is applied to the field windings, and the higher power output comes from the armature windings. (See Excitation (magnetic) for how a generator can act as an amplifier.) The amplifier output is usually connected to a second motor, which moves the load, such as an elevator. With this arrangement, small changes in current applied to the input, and thus the generator field, result in large changes in the output, allowing smooth speed control.

A flywheel may be used to reduce voltage fluctuations during sudden load changes. The Ward Leonard system with this modification is known as Ward Leonard Ilgner Control. In that configuration, the synchronous motor, normally used for Ward Leonard control, is replaced by a wound-rotor induction motor. The combination of an induction motor, flywheel, and generator(s) is known as an Ilgner set. It effectively decouples intermittent short-term high loading of the generator from the AC supply.

A more technical description

A Ward Leonard Control system with generator and motor connected directly.

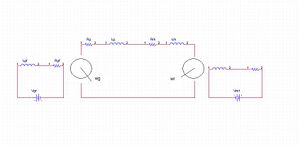
The speed of a DC motor is controlled by varying the voltage fed to the generator field windings, V_gf, which varies the output voltage of the generator. The varied output voltage will change the voltage of the motor, since they are connected directly through the armature. Consequently, changing the V_gf will control the speed of the motor. The picture on the right shows the Ward Leonard control system, with the V_gf feeding the generator and V_mf feeding the motor.

Transfer function

The first subscripts 'g' and 'm' each represents generator and motor. The superscripts 'f', 'r',and 'a', correspond to field, rotor, and armature.

• [math]\displaystyle{ W_i }[/math] = plant state vector
• [math]\displaystyle{ K }[/math] = gain
• [math]\displaystyle{ t }[/math] = time constant
• [math]\displaystyle{ J }[/math] = polar moment of inertia
• [math]\displaystyle{ D }[/math] = angular viscous friction
• [math]\displaystyle{ G }[/math] = rotational inductance constant
• [math]\displaystyle{ s }[/math] = Laplace operator

Eq. 1: The generator field equation

[math]\displaystyle{ V_g^f = R_g^f I_g^f + L_g^f I_g^f }[/math]

Eq. 2: The equation of electrical equilibrium in the armature circuit

[math]\displaystyle{ -G_g^fa I_g^f W_g^r + (R_g^a + R_m^a) I^a + (L_g^a + L_m^a) I^a + G_m^fa I_m^f W_m^r = 0 }[/math]

Eq. 3: Motor torque equation

[math]\displaystyle{ -T_L = J_m W_m^r + D_mW_m^r }[/math]

With total impedance, [math]\displaystyle{ L_g^a + L_m^a }[/math], neglected, the transfer function can be obtained by solving eq 3 [math]\displaystyle{ T_L = 0 }[/math].

Eq. 4: Transfer function

[math]\displaystyle{ \frac{W_m^r(S)}{V_g^f(S)} = \cfrac{K_BK_v/D_m}{\left(t_g^fs + 1\right)\left(t_ms + \frac{K_m}{D_m}\right)} }[/math]

with the constants defined as below:

[math]\displaystyle{ K_B = \frac{G_m^fa V_m^f}{R_m^f(R_g^a + R_m^a)} }[/math]

[math]\displaystyle{ K_v = \frac{G_g^fa W_g^r}{R_g^f} }[/math]

[math]\displaystyle{ t_m = \frac{J_m}{D_m} }[/math]

[math]\displaystyle{ t_g^f = \frac{L_g^f}{R_g^f} }[/math]

[math]\displaystyle{ K_m = D_m + K_B^2(R_g^a + R_m^a) }[/math]

See also

• Adjustable-speed drive
• Amplidyne, an electromechanical amplifier invented during World War II
• Brushed DC electric motor
• Electric motor
• Electronic speed control
• Harry Ward Leonard
• Metadyne
• Motor controller
• Motor-generator

References

Citations

General references

• The Editors (Nov 1989). "Technology for Electrical Components". Power Transmission Design: 25–27. 
• Ward Leonard, H. (1896). "Volts versus ohms - the speed regulation of electric motors". AIEE Trans. 13: 375–384. 
• Gottlieb, I.M. (1994). Electric Motors & Control Techniques 2nd Edition. TAB Books. 
• Malcolm Barnes (2003). Practical Variable Speed Drives and Power Electronics. Oxford: Newnes. pp. 20–21. ISBN 978-0-7506-5808-9. https://books.google.com/books?id=8mQewRR_3q4C&q=%22ward+leonard%22+drive&pg=RA1-PA20. 

de:Umformer#Leonardsatz