Fast inverse square root

Short description: Root-finding algorithm

Lighting and reflection calculations, as in the video game OpenArena, use the fast inverse square root code to compute angles of incidence and reflection.

Fast inverse square root, sometimes referred to as Fast InvSqrt() or by the hexadecimal constant 0x5F3759DF, is an algorithm that estimates [math]\displaystyle{ \frac{1}{\sqrt{x}} }[/math], the reciprocal (or multiplicative inverse) of the square root of a 32-bit floating-point number [math]\displaystyle{ x }[/math] in IEEE 754 floating-point format. The algorithm is best known for its implementation in 1999 in Quake III Arena, a first-person shooter video game heavily based on 3D graphics. With subsequent hardware advancements, especially the x86 SSE instruction rsqrtss, this algorithm is not generally the best choice for modern computers, though it remains an interesting historical example.

The algorithm accepts a 32-bit floating-point number as the input and stores a halved value for later use. Then, treating the bits representing the floating-point number as a 32-bit integer, a logical shift right by one bit is performed and the result subtracted from the number 0x5F3759DF, which is a floating-point representation of an approximation of [math]\displaystyle{ \sqrt{2^{127}} }[/math]. This results in the first approximation of the inverse square root of the input. Treating the bits again as a floating-point number, it runs one iteration of Newton's method, yielding a more precise approximation.

History

William Kahan and K.C. Ng at Berkeley wrote an unpublished paper in May 1986 describing how to calculate the square root using bit-fiddling techniques followed by Newton iterations. In the late 1980s, Cleve Moler at Ardent Computer learned about this technique and passed it along to his coworker Greg Walsh. Greg Walsh devised the now-famous constant and fast inverse square root algorithm. Gary Tarolli was consulting for Kubota, the company funding Ardent at the time, and likely brought the algorithm to 3dfx Interactive circa 1994.

Jim Blinn demonstrated a simple approximation of the inverse square root in a 1997 column for IEEE Computer Graphics and Applications. Reverse engineering of other contemporary 3D video games uncovered a variation of the algorithm in Activision's 1997 Interstate '76.

Quake III Arena, a first-person shooter video game, was released in 1999 by id Software and used the algorithm. Brian Hook may have brought the algorithm from 3dfx to id Software. A discussion of the code appeared on the Chinese developer forum CSDN in 2000, and Usenet and the gamedev.net forum spread the code widely in 2002 and 2003. Speculation arose as to who wrote the algorithm and how the constant was derived; some guessed John Carmack. Quake III's full source code was released at QuakeCon 2005, but provided no answers. The authorship question was answered in 2006 when Greg Walsh contacted Beyond3D as their speculation gained popularity on Slashdot.

In 2007 the algorithm was implemented in some dedicated hardware vertex shaders using field-programmable gate arrays (FPGA).

Motivation

Surface normals are used extensively in lighting and shading calculations, requiring the calculation of norms for vectors. A field of vectors normal to a surface is shown here.

A two-dimensional example of using the normal [math]\displaystyle{ C }[/math] to find the angle of reflection from the angle of incidence; in this case, on light reflecting from a curved mirror. The fast inverse square root is used to generalize this calculation to three-dimensional space.

The inverse square root of a floating point number is used in digital signal processing to normalize a vector, scaling it to length 1 to produce a unit vector. For example, computer graphics programs use inverse square roots to compute angles of incidence and reflection for lighting and shading. 3D graphics programs must perform millions of these calculations every second to simulate lighting. When the code was developed in the early 1990s, most floating point processing power lagged the speed of integer processing. This was troublesome for 3D graphics programs before the advent of specialized hardware to handle transform and lighting. Computation of square roots usually depends upon many division operations, which for floating point numbers are computationally expensive. The fast inverse square generates a good approximation with only one division step.

The length of the vector is determined by calculating its Euclidean norm: the square root of the sum of squares of the vector components. When each component of the vector is divided by that length, the new vector will be a unit vector pointing in the same direction. In a 3D graphics program, all vectors are in three-dimensional space, so [math]\displaystyle{ \boldsymbol v }[/math] would be a vector [math]\displaystyle{ (v_1, v_2, v_3) }[/math].

[math]\displaystyle{ \|\boldsymbol{v}\| = \sqrt{v_1^2+v_2^2+v_3^2} }[/math]

is the Euclidean norm of the vector.

[math]\displaystyle{ \boldsymbol{\hat{v}} = \frac{\boldsymbol{v}}{\left\|\boldsymbol{v}\right\|} }[/math]

is the normalized (unit) vector. Substituting [math]\displaystyle{ \|\boldsymbol v\| }[/math], the equation can also be written as:

[math]\displaystyle{ \boldsymbol{\hat{v}} = \frac{\boldsymbol{v}}\sqrt{v_1^2+v_2^2+v_3^2} }[/math]

which relates the unit vector to the inverse square root of the distance components. The inverse square root can be used to compute [math]\displaystyle{ \boldsymbol{\hat{v}} }[/math] because this equation is equivalent to

[math]\displaystyle{ \boldsymbol{\hat{v}} = \boldsymbol{v}\, \frac{1}\sqrt{v_1^2+v_2^2+v_3^2} }[/math]

where the fraction term is the inverse square root of [math]\displaystyle{ v_1^2+v_2^2+v_3^2 }[/math].

At the time, floating-point division was generally expensive compared to multiplication; the fast inverse square root algorithm bypassed the division step, giving it its performance advantage.

Overview of the code

The following code is the fast inverse square root implementation from Quake III Arena, stripped of C preprocessor directives, but including the exact original comment text:

float q_rsqrt(float number)
{
  long i;
  float x2, y;
  const float threehalfs = 1.5F;

  x2 = number * 0.5F;
  y  = number;
  i  = * ( long * ) &y;                       // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
  y  = * ( float * ) &i;
  y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

  return y;
}

At the time, the general method to compute the inverse square root was to calculate an approximation for [math]\displaystyle{ \frac{1}{\sqrt{x}} }[/math], then revise that approximation via another method until it came within an acceptable error range of the actual result. Common software methods in the early 1990s drew approximations from a lookup table. The key of the fast inverse square root was to directly compute an approximation by utilizing the structure of floating-point numbers, proving faster than table lookups. The algorithm was approximately four times faster than computing the square root with another method and calculating the reciprocal via floating-point division. The algorithm was designed with the IEEE 754-1985 32-bit floating-point specification in mind, but investigation from Chris Lomont showed that it could be implemented in other floating-point specifications.

The advantages in speed offered by the fast inverse square root trick came from treating the 32-bit floating-point word as an integer, then subtracting it from a "magic" constant, 0x5F3759DF. This integer subtraction and bit shift results in a bit pattern which, when re-defined as a floating-point number, is a rough approximation for the inverse square root of the number. One iteration of Newton's method is performed to gain some accuracy, and the code is finished. The algorithm generates reasonably accurate results using a unique first approximation for Newton's method; however, it is much slower and less accurate than using the SSE instruction rsqrtss on x86 processors also released in 1999.

Worked example

As an example, the number [math]\displaystyle{ x=0.15625 }[/math] can be used to calculate [math]\displaystyle{ \frac{1}{\sqrt{x}} \approx 2.52982 }[/math]. The first steps of the algorithm are illustrated below:

0011_1110_0010_0000_0000_0000_0000_0000  Bit pattern of both x and i
0001_1111_0001_0000_0000_0000_0000_0000  Shift right one position: (i >> 1)
0101_1111_0011_0111_0101_1001_1101_1111  The magic number 0x5F3759DF
0100_0000_0010_0111_0101_1001_1101_1111  The result of 0x5F3759DF - (i >> 1)

Interpreting as IEEE 32-bit representation:

0_01111100_01000000000000000000000  1.25 × 2−3
0_00111110_00100000000000000000000  1.125 × 2−65
0_10111110_01101110101100111011111  1.432430... × 263
0_10000000_01001110101100111011111  1.307430... × 21

Reinterpreting this last bit pattern as a floating point number gives the approximation [math]\displaystyle{ y=2.61486 }[/math], which has an error of about 3.4%. After one single iteration of Newton's method, the final result is [math]\displaystyle{ y=2.52549 }[/math], an error of only 0.17%.

Avoiding undefined behavior

According to the C standard, reinterpreting a floating point value as an integer by casting then dereferencing the pointer to it is not valid (undefined behavior). Another way would be to place the floating point value in an anonymous union containing an additional 32-bit unsigned integer member, and accesses to that integer provides a bit level view of the contents of the floating point value. However, type punning through a union is also undefined behavior in C++.

# include <stdint.h> // uint32_t

float q_rsqrt(float number)
{
  union {
    float    f;
    uint32_t i;
  } conv = { .f = number };
  conv.i  = 0x5f3759df - (conv.i >> 1);
  conv.f *= 1.5F - (number * 0.5F * conv.f * conv.f);
  return conv.f;
}

In modern C++, the usual method for implementing this function's casts is through C++20's std::bit_cast. This also allows the function to work in constexpr context:

# include <bit>
# include <limits>
# include <cstdint>

constexpr float Q_rsqrt(float number) noexcept
{
  static_assert(std::numeric_limits<float>::is_iec559); // (enable only on IEEE 754)

  float const y = std::bit_cast<float>(
    0x5f3759df - (std::bit_cast<std::uint32_t>(number) >> 1));
  return y * (1.5f - (number * 0.5f * y * y));
}

Algorithm

The algorithm computes [math]\displaystyle{ \frac{1}{\sqrt{x}} }[/math] by performing the following steps:

1. Alias the argument [math]\displaystyle{ x }[/math] to an integer as a way to compute an approximation of the binary logarithm [math]\displaystyle{ \log_{2}(x) }[/math]
2. Use this approximation to compute an approximation of [math]\displaystyle{ \log_{2}\left(\frac{1}{\sqrt{x}}\right) = -\frac{1}{2} \log_{2}(x) }[/math]
3. Alias back to a float, as a way to compute an approximation of the base-2 exponential
4. Refine the approximation using a single iteration of Newton's method.

Floating-point representation

Since this algorithm relies heavily on the bit-level representation of single-precision floating-point numbers, a short overview of this representation is provided here. To encode a non-zero real number [math]\displaystyle{ x }[/math] as a single precision float, the first step is to write [math]\displaystyle{ x }[/math] as a normalized binary number:

[math]\displaystyle{ \begin{align} x &= \pm 1.b_1b_2b_3\ldots \times 2^{e_x} \end{align} }[/math]

where the exponent [math]\displaystyle{ e_x }[/math] is an integer, and [math]\displaystyle{ 1.b_1b_2b_3\ldots }[/math] is the binary representation of the significand. Since the single bit before the point in the significand is always 1, it does not need be stored. The equation can be rewritten as:

[math]\displaystyle{ \begin{align} x &= \pm 2^{e_x} (1 + m_x) \end{align} }[/math]

where [math]\displaystyle{ m_x }[/math] means [math]\displaystyle{ 0.b_1b_2b_3\ldots }[/math], so [math]\displaystyle{ m_x \in [0, 1) }[/math]. From this form, three unsigned integers are computed:

• [math]\displaystyle{ S_x }[/math], the "sign bit", is [math]\displaystyle{ 0 }[/math] if [math]\displaystyle{ x }[/math] is positive and [math]\displaystyle{ 1 }[/math] negative or zero (1 bit)
• [math]\displaystyle{ E_x = e_x + B }[/math] is the "biased exponent", where [math]\displaystyle{ B = 127 }[/math] is the "exponent bias" (8 bits)
• [math]\displaystyle{ M_x = m_x \times L }[/math], where [math]\displaystyle{ L = 2^{23} }[/math] (23 bits)

These fields are then packed, left to right, into a 32-bit container.

As an example, consider again the number [math]\displaystyle{ x = 0.15625 = 0.00101_2 }[/math]. Normalizing [math]\displaystyle{ x }[/math] yields:

[math]\displaystyle{ x = +2^{-3}(1 + 0.25) }[/math]

and thus, the three unsigned integer fields are:

• [math]\displaystyle{ S = 0 }[/math]
• [math]\displaystyle{ E = -3 + 127 = 124 = 0111\ 1100_2 }[/math]
• [math]\displaystyle{ M = 0.25 \times 2^{23} = 2\ 097\ 152 = 0010\ 0000\ 0000\ 0000\ 0000\ 0000_2 }[/math]

these fields are packed as shown in the figure below:

Aliasing to an integer as an approximate logarithm

If [math]\displaystyle{ \frac{1}{\sqrt{x}} }[/math] were to be calculated without a computer or a calculator, a table of logarithms would be useful, together with the identity [math]\displaystyle{ \log_b\left(\frac{1}{\sqrt{x}}\right) = \log_b\left(x^{-\frac{1}{2}}\right) = -\frac{1}{2} \log_b(x) }[/math], which is valid for every base [math]\displaystyle{ b }[/math]. The fast inverse square root is based on this identity, and on the fact that aliasing a float32 to an integer gives a rough approximation of its logarithm. Here is how:

If [math]\displaystyle{ x }[/math] is a positive normal number:

[math]\displaystyle{ x = 2^{e_x} (1 + m_x) }[/math]

then

[math]\displaystyle{ \log_2(x) = e_x + \log_2(1 + m_x) }[/math]

and since [math]\displaystyle{ m_x \in [0, 1) }[/math], the logarithm on the right-hand side can be approximated by

[math]\displaystyle{ \log_2(1 + m_x) \approx m_x + \sigma }[/math]

where [math]\displaystyle{ \sigma }[/math] is a free parameter used to tune the approximation. For example, [math]\displaystyle{ \sigma = 0 }[/math] yields exact results at both ends of the interval, while [math]\displaystyle{ \sigma = \frac{1}{2} - \frac{1+\ln(\ln(2))}{2\ln(2)} \approx 0.0430357 }[/math] yields the optimal approximation (the best in the sense of the uniform norm of the error). However, this value is not used by the algorithm as it does not take subsequent steps into account.

The integer aliased to a floating point number (in blue), compared to a scaled and shifted logarithm (in gray).

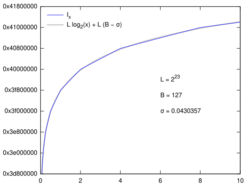
Thus there is the approximation

[math]\displaystyle{ \log_2(x) \approx e_x + m_x + \sigma. }[/math]

Interpreting the floating-point bit-pattern of [math]\displaystyle{ x }[/math] as an integer [math]\displaystyle{ I_x }[/math] yields

[math]\displaystyle{ \begin{align} I_x &= E_x L + M_x\\ &= L (e_x + B + m_x)\\ &= L (e_x + m_x + \sigma + B - \sigma)\\ &\approx L \log_2(x) + L (B - \sigma). \end{align} }[/math]

It then appears that [math]\displaystyle{ I_x }[/math] is a scaled and shifted piecewise-linear approximation of [math]\displaystyle{ \log_2(x) }[/math], as illustrated in the figure on the right. In other words, [math]\displaystyle{ \log_2(x) }[/math] is approximated by

[math]\displaystyle{ \log_2(x) \approx \frac{I_x}{L} - (B - \sigma). }[/math]

First approximation of the result

The calculation of [math]\displaystyle{ y=\frac{1}{\sqrt{x}} }[/math] is based on the identity

[math]\displaystyle{ \log_2(y) = - \tfrac{1}{2}\log_2(x) }[/math]

Using the approximation of the logarithm above, applied to both [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math], the above equation gives:

[math]\displaystyle{ \frac{I_y}{L} - (B - \sigma) \approx - \frac{1}{2}\left(\frac{I_x}{L} - (B - \sigma)\right) }[/math]

Thus, an approximation of [math]\displaystyle{ I_y }[/math] is:

[math]\displaystyle{ I_y \approx \tfrac{3}{2} L (B - \sigma) - \tfrac{1}{2} I_x }[/math]

which is written in the code as

i  = 0x5f3759df - ( i >> 1 );

The first term above is the magic number

[math]\displaystyle{ \tfrac{3}{2} L (B - \sigma) = \mathtt{0x5F3759DF} }[/math]

from which it can be inferred that [math]\displaystyle{ \sigma \approx 0.0450466 }[/math]. The second term, [math]\displaystyle{ \frac{1}{2}I_x }[/math], is calculated by shifting the bits of [math]\displaystyle{ I_x }[/math] one position to the right.

Newton's method

Relative error between direct calculation and fast inverse square root carrying out 0, 1, 2, 3, and 4 iterations of Newton's root-finding method. Note that double precision is adopted and the smallest representable difference between two double precision numbers is reached after carrying out 4 iterations.

With [math]\displaystyle{ y }[/math] as the inverse square root, [math]\displaystyle{ f(y)=\frac{1}{y^2}-x=0 }[/math]. The approximation yielded by the earlier steps can be refined by using a root-finding method, a method that finds the zero of a function. The algorithm uses Newton's method: if there is an approximation, [math]\displaystyle{ y_n }[/math] for [math]\displaystyle{ y }[/math], then a better approximation [math]\displaystyle{ y_{n+1} }[/math] can be calculated by taking [math]\displaystyle{ y_n - \frac{f(y_n)}{f'(y_n)} }[/math], where [math]\displaystyle{ f'(y_n) }[/math] is the derivative of [math]\displaystyle{ f(y) }[/math] at [math]\displaystyle{ y_n }[/math]. For the above [math]\displaystyle{ f(y) }[/math],

[math]\displaystyle{ y_{n+1} = \frac{y_{n}\left(3-xy_n^2\right)}{2} }[/math]

where [math]\displaystyle{ f(y)= \frac{1}{y^2} - x }[/math] and [math]\displaystyle{ f'(y) = -\frac{2}{y^3} }[/math].

Treating [math]\displaystyle{ y }[/math] as a floating-point number, y = y*(threehalfs - x/2*y*y); is equivalent to

[math]\displaystyle{ y_{n+1} = y_{n}\left (\frac32-\frac{x}{2}y_n^2\right ) = \frac{y_{n}\left(3-xy_n^2\right)}{2}. }[/math]

By repeating this step, using the output of the function ([math]\displaystyle{ y_{n+1} }[/math]) as the input of the next iteration, the algorithm causes [math]\displaystyle{ y }[/math] to converge to the inverse square root. For the purposes of the Quake III engine, only one iteration was used. A second iteration remained in the code but was commented out.

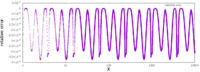
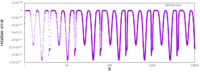
Accuracy

As noted above, the approximation is very accurate. The single graph on the right plots the error of the function (that is, the error of the approximation after it has been improved by running one iteration of Newton's method), for inputs starting at 0.01, where the standard library gives 10.0 as a result, and InvSqrt() gives 9.982522, making the relative difference 0.0017478, or 0.175% of the true value, 10. The absolute error only drops from then on, and the relative error stays within the same bounds across all orders of magnitude.

Subsequent improvements

Magic number

It is not known precisely how the exact value for the magic number was determined. Chris Lomont developed a function to minimize approximation error by choosing the magic number [math]\displaystyle{ R }[/math] over a range. He first computed the optimal constant for the linear approximation step as 0x5F37642F, close to 0x5F3759DF, but this new constant gave slightly less accuracy after one iteration of Newton's method. Lomont then searched for a constant optimal even after one and two Newton iterations and found 0x5F375A86, which is more accurate than the original at every iteration stage. He concluded by asking whether the exact value of the original constant was chosen through derivation or trial and error. Lomont said that the magic number for 64-bit IEEE754 size type double is 0x5FE6EC85E7DE30DA, but it was later shown by Matthew Robertson to be exactly 0x5FE6EB50C7B537A9.

Jan Kadlec reduced the relative error by a further factor of 2.7 by adjusting the constants in the single Newton's method iteration as well, arriving after an exhaustive search at

conv.i = 0x5F1FFFF9 - ( conv.i >> 1 );
conv.f *= 0.703952253f * ( 2.38924456f - x * conv.f * conv.f );
return conv.f;

A complete mathematical analysis for determining the magic number is now available for single-precision floating-point numbers.

Zero finding

Intermediate to the use of one vs. two iterations of Newton's method in terms of speed and accuracy is a single iteration of Halley's method. In this case, Halley's method is equivalent to applying Newton's method with the starting formula [math]\displaystyle{ f(y) = \frac{1}{y^{1/2}} - xy^{3/2} = 0 }[/math]. The update step is then

[math]\displaystyle{ y_{n+1} = y_{n} - \frac{f(y_n)}{f'(y_n)} = y_n \left(\frac{3 + xy_n^2}{1 + 3xy_n^2}\right), }[/math]

where the implementation should calculate [math]\displaystyle{ xy_n^2 }[/math] only once, via a temporary variable.

Obsolescence

Subsequent additions by hardware manufacturers have made this algorithm redundant for the most part. For example, on x86, Intel introduced the SSE instruction rsqrtss in 1999. In a 2009 benchmark on the Intel Core 2, this instruction took 0.85ns per float compared to 3.54ns for the fast inverse square root algorithm, and had less error.

Some low-cost embedded systems do not have specialized square root instructions. However, manufacturers of these systems usually provide trigonometric and other math libraries, based on algorithms such as CORDIC. Most applications in this area are not performance-sensitive and a specialized fast inverse square root algorithm is not needed.

See also

• Methods of computing square roots § Approximations that depend on the floating point representation
• Magic number

References

Bibliography

• Blinn, Jim (July 1997). "Floating Point Tricks". IEEE Computer Graphics & Applications 17 (4): 80. doi:10.1109/38.595279. 
• Blinn, Jim (2003). Jim Blinn's Corner: Notation, notation notation. Morgan Kaufmann. ISBN 1-55860-860-5. 
• Eberly, David (2001). 3D Game Engine Design. Morgan Kaufmann. ISBN 978-1-55860-593-0. https://archive.org/details/isbn_9781558605930. 
• Goldberg, David (1991). "What every computer scientist should know about floating-point arithmetic". ACM Computing Surveys 23 (1): 5–48. doi:10.1145/103162.103163. 
• Hardy, Godfrey (1908). A Course of Pure Mathematics. Cambridge, UK: Cambridge University Press. ISBN 0-521-72055-9. http://www.gutenberg.org/files/38769. 
• Hennessey, John; Patterson, David A. (1998). Computer Organization and Design (2nd ed.). San Francisco, CA: Morgan Kaufmann Publishers. ISBN 978-1-55860-491-9. https://archive.org/details/computerorganiz000henn. 
• Lomont, Chris (February 2003). "Fast Inverse Square Root". http://www.lomont.org/Math/Papers/2003/InvSqrt.pdf. 
• McEniry, Charles (August 2007). "The Mathematics Behind the Fast Inverse Square Root Function Code". http://www.daxia.com/bibis/upload/406Fast_Inverse_Square_Root.pdf. 
• Middendorf, Lars; Mühlbauer, Felix; Umlauf, George; Bodba, Christophe (June 1, 2007). "Embedded Vertex Shader in FPGA". in Rettberg, Achin. IFIP TC10 Working Conference:International Embedded Systems Symposium (IESS). et al.. Irvine, California: Springer. doi:10.1007/978-0-387-72258-0_14. ISBN 978-0-387-72257-3. https://link.springer.com/content/pdf/10.1007/978-0-387-72258-0_14.pdf. 
• Striegel, Jason (2008-12-04). "Quake's fast inverse square root". Hackszine. O'Reilly Media. http://www.hackszine.com/blog/archive/2008/12/quakes_fast_inverse_square_roo.html. 
• IEEE Computer Society (1985), 754-1985 - IEEE Standard for Binary Floating-Point Arithmetic, Institute of Electrical and Electronics Engineers, https://standards.ieee.org/findstds/standard/754-1985.html 
• Moroz, Leonid V.; Walczyk, Cezary J.; Hrynchyshyn, Andriy; Holimath, Vijay; Cieslinski, Jan L. (January 2018). "Fast calculation of inverse square root with the use of magic constant analytical approach". Applied Mathematics and Computation (Elsevier Science Inc.) 316 (C): 245–255. doi:10.1016/j.amc.2017.08.025. 

Further reading

• Kushner, David (August 2002). "The wizardry of Id". IEEE Spectrum 39 (8): 42–47. doi:10.1109/MSPEC.2002.1021943. 

External links

• 0x5f3759df, further investigations into accuracy and generalizability of the algorithm by Christian Plesner Hansen
• Origin of Quake3's Fast InvSqrt()
• Quake III Arena source code (archived in Software Heritage)
• Implementation of InvSqrt in DESMOS
• "Fast Inverse Square Root — A Quake III Algorithm" (YouTube)