Fence (mathematics)

From HandWiki
Short description: Partially ordered set with alternatingly-related elements
The Hasse diagram of a six-element fence.

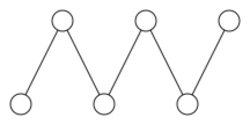
In mathematics, a fence, also called a zigzag poset, is a partially ordered set (poset) in which the order relations form a path with alternating orientations:

[math]\displaystyle{ a\lt b\gt c\lt d\gt e\lt f\gt h\lt i \cdots }[/math]

or

[math]\displaystyle{ a\gt b\lt c\gt d\lt e\gt f\lt h\gt i \cdots }[/math]

A fence may be finite, or it may be formed by an infinite alternating sequence extending in both directions. The incidence posets of path graphs form examples of fences.

A linear extension of a fence is called an alternating permutation; André's problem of counting the number of different linear extensions has been studied since the 19th century.[1] The solutions to this counting problem, the so-called Euler zigzag numbers or up/down numbers, are:

[math]\displaystyle{ 1, 1, 2, 4, 10, 32, 122, 544, 2770, 15872, 101042. }[/math]
(sequence A001250 in the OEIS).

The number of antichains in a fence is a Fibonacci number; the distributive lattice with this many elements, generated from a fence via Birkhoff's representation theorem, has as its graph the Fibonacci cube.[2]

A partially ordered set is series-parallel if and only if it does not have four elements forming a fence.[3]

Several authors have also investigated the number of order-preserving maps from fences to themselves, or to fences of other sizes.[4]

An up-down poset Q(a,b) is a generalization of a zigzag poset in which there are a downward orientations for every upward one and b total elements.[5] For instance, Q(2,9) has the elements and relations

[math]\displaystyle{ a\gt b\gt c\lt d\gt e\gt f\lt g\gt h\gt i. }[/math]

In this notation, a fence is a partially ordered set of the form Q(1,n).

Equivalent conditions

The following conditions are equivalent for a poset P:[citation needed]

  1. P is a disjoint union of zigzag posets.
  2. If a ≤ b ≤ c in P, either a = b or b = c.
  3. [math]\displaystyle{ \lt \circ \lt \; = \emptyset }[/math], i.e. it is never the case that a < b and b < c, so that < is vacuously transitive.
  4. P has dimension at most one (defined analogously to the Krull dimension of a commutative ring).
  5. Every element of P is either maximal or minimal.
  6. The slice category Pos/P is cartesian closed.[lower-alpha 1]

The prime ideals of a commutative ring R, ordered by inclusion, satisfy the equivalent conditions above if and only if R has Krull dimension at most one.[citation needed]

Notes

  1. ↑ Here, Pos denotes the category of partially ordered sets.

References

  1. ↑ (André 1881).
  2. ↑ (Gansner 1982) calls the fact that this lattice has a Fibonacci number of elements a “well known fact,” while (Stanley 1986) asks for a description of it in an exercise. See also (Höft Höft), (Beck 1990), and (Salvi Salvi).
  3. ↑ (Valdes Tarjan).
  4. ↑ (Currie Visentin); (Duffus Rödl); (Rutkowski 1992a); (Rutkowski 1992b); (Farley 1995).
  5. ↑ (Gansner 1982).
  • André, Désiré (1881), "Sur les permutations alternées", J. Math. Pures Appl., (Ser. 3) 7: 167–184 .
  • Beck, István (1990), "Partial orders and the Fibonacci numbers", Fibonacci Quarterly 28 (2): 172–174 .
  • Currie, J. D.; Visentin, T. I. (1991), "The number of order-preserving maps of fences and crowns", Order 8 (2): 133–142, doi:10.1007/BF00383399 .
  • "Enumeration of order preserving maps", Order 9 (1): 15–29, 1992, doi:10.1007/BF00419036 .
  • Farley, Jonathan David (1995), "The number of order-preserving maps between fences and crowns", Order 12 (1): 5–44, doi:10.1007/BF01108588 .
  • Gansner, Emden R. (1982), "On the lattice of order ideals of an up-down poset", Discrete Mathematics 39 (2): 113–122, doi:10.1016/0012-365X(82)90134-0 .
  • Höft, Hartmut; Höft, Margret (1985), "A Fibonacci sequence of distributive lattices", Fibonacci Quarterly 23 (3): 232–237 .
  • Kelly, David (1974), "Crowns, fences, and dismantlable lattices", Canadian Journal of Mathematics 26 (5): 1257–1271, doi:10.4153/cjm-1974-120-2 .
  • Rutkowski, Aleksander (1992a), "The number of strictly increasing mappings of fences", Order 9 (1): 31–42, doi:10.1007/BF00419037 .
  • Rutkowski, Aleksander (1992b), "The formula for the number of order-preserving self-mappings of a fence", Order 9 (2): 127–137, doi:10.1007/BF00814405 .
  • Salvi, Rodolfo; Salvi, Norma Zagaglia (2008), "Alternating unimodal sequences of Whitney numbers", Ars Combinatoria 87: 105–117 .
  • Enumerative Combinatorics, Wadsworth, Inc., 1986  Exercise 3.23a, page 157.
  • Valdes, Jacobo (1982), "The Recognition of Series Parallel Digraphs", SIAM Journal on Computing 11 (2): 298–313, doi:10.1137/0211023 .

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Fence_(mathematics)&oldid=3381026"