Disjoint union
This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations. (January 2022) (Learn how and when to remove this template message) |
 | |
| Type | Set operation |
|---|---|
| Field | Set theory |
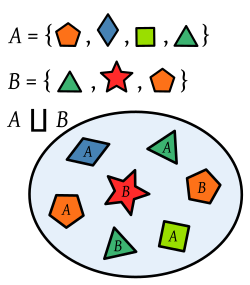
In mathematics, the disjoint union (or discriminated union) [math]\displaystyle{ A \sqcup B }[/math] of the sets A and B is the set formed from the elements of A and B labelled (indexed) with the name of the set from which they come. So, an element belonging to both A and B appears twice in the disjoint union, with two different labels.
A disjoint union of an indexed family of sets [math]\displaystyle{ (A_i : i\in I) }[/math] is a set [math]\displaystyle{ A, }[/math] often denoted by [math]\displaystyle{ \bigsqcup_{i \in I} A_i, }[/math] with an injection of each [math]\displaystyle{ A_i }[/math] into [math]\displaystyle{ A, }[/math] such that the images of these injections form a partition of [math]\displaystyle{ A }[/math] (that is, each element of [math]\displaystyle{ A }[/math] belongs to exactly one of these images). A disjoint union of a family of pairwise disjoint sets is their union.
In category theory, the disjoint union is the coproduct of the category of sets, and thus defined up to a bijection. In this context, the notation [math]\displaystyle{ \coprod_{i\in I} A_i }[/math] is often used.
The disjoint union of two sets [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] is written with infix notation as [math]\displaystyle{ A \sqcup B }[/math]. Some authors use the alternative notation [math]\displaystyle{ A \uplus B }[/math] or [math]\displaystyle{ A \operatorname{{\cup}\!\!\!{\cdot}\,} B }[/math] (along with the corresponding [math]\displaystyle{ \biguplus_{i\in I} A_i }[/math] or [math]\displaystyle{ \operatorname{{\bigcup}\!\!\!{\cdot}\,}_{i\in I} A_i }[/math]).
A standard way for building the disjoint union is to define [math]\displaystyle{ A }[/math] as the set of ordered pairs [math]\displaystyle{ (x, i) }[/math] such that [math]\displaystyle{ x \in A_i, }[/math] and the injection [math]\displaystyle{ A_i \to A }[/math] as [math]\displaystyle{ x \mapsto (x, i). }[/math]
Example
Consider the sets [math]\displaystyle{ A_0 = \{5, 6, 7\} }[/math] and [math]\displaystyle{ A_1 = \{5, 6\}. }[/math] It is possible to index the set elements according to set origin by forming the associated sets [math]\displaystyle{ \begin{align} A^*_0 & = \{(5, 0), (6, 0), (7, 0)\} \\ A^*_1 & = \{(5, 1), (6, 1)\}, \\ \end{align} }[/math]
where the second element in each pair matches the subscript of the origin set (for example, the [math]\displaystyle{ 0 }[/math] in [math]\displaystyle{ (5, 0) }[/math] matches the subscript in [math]\displaystyle{ A_0, }[/math] etc.). The disjoint union [math]\displaystyle{ A_0 \sqcup A_1 }[/math] can then be calculated as follows: [math]\displaystyle{ A_0 \sqcup A_1 = A^*_0 \cup A^*_1 = \{(5, 0), (6, 0), (7, 0), (5, 1), (6, 1)\}. }[/math]
Set theory definition
Formally, let [math]\displaystyle{ \left(A_i : i \in I\right) }[/math] be an indexed family of sets indexed by [math]\displaystyle{ I. }[/math] The disjoint union of this family is the set [math]\displaystyle{ \bigsqcup_{i \in I} A_i = \bigcup_{i \in I} \left\{(x, i) : x \in A_i\right\}. }[/math] The elements of the disjoint union are ordered pairs [math]\displaystyle{ (x, i). }[/math] Here [math]\displaystyle{ i }[/math] serves as an auxiliary index that indicates which [math]\displaystyle{ A_i }[/math] the element [math]\displaystyle{ x }[/math] came from.
Each of the sets [math]\displaystyle{ A_i }[/math] is canonically isomorphic to the set [math]\displaystyle{ A_i^* = \left\{(x,i) : x \in A_i\right\}. }[/math] Through this isomorphism, one may consider that [math]\displaystyle{ A_i }[/math] is canonically embedded in the disjoint union. For [math]\displaystyle{ i \neq j, }[/math] the sets [math]\displaystyle{ A_i^* }[/math] and [math]\displaystyle{ A_j^* }[/math] are disjoint even if the sets [math]\displaystyle{ A_i }[/math] and [math]\displaystyle{ A_j }[/math] are not.
In the extreme case where each of the [math]\displaystyle{ A_i }[/math] is equal to some fixed set [math]\displaystyle{ A }[/math] for each [math]\displaystyle{ i \in I, }[/math] the disjoint union is the Cartesian product of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ I }[/math]: [math]\displaystyle{ \bigsqcup_{i \in I} A_i = A \times I. }[/math]
Occasionally, the notation [math]\displaystyle{ \sum_{i \in I} A_i }[/math] is used for the disjoint union of a family of sets, or the notation [math]\displaystyle{ A + B }[/math] for the disjoint union of two sets. This notation is meant to be suggestive of the fact that the cardinality of the disjoint union is the sum of the cardinalities of the terms in the family. Compare this to the notation for the Cartesian product of a family of sets.
In the language of category theory, the disjoint union is the coproduct in the category of sets. It therefore satisfies the associated universal property. This also means that the disjoint union is the categorical dual of the Cartesian product construction. See Coproduct for more details.
For many purposes, the particular choice of auxiliary index is unimportant, and in a simplifying abuse of notation, the indexed family can be treated simply as a collection of sets. In this case [math]\displaystyle{ A_i^* }[/math] is referred to as a copy of [math]\displaystyle{ A_i }[/math] and the notation [math]\displaystyle{ \underset{A \in C}{\,\,\bigcup\nolimits^{*}\!} A }[/math] is sometimes used.
Category theory point of view
In category theory the disjoint union is defined as a coproduct in the category of sets.
As such, the disjoint union is defined up to an isomorphism, and the above definition is just one realization of the coproduct, among others. When the sets are pairwise disjoint, the usual union is another realization of the coproduct. This justifies the second definition in the lead.
This categorical aspect of the disjoint union explains why [math]\displaystyle{ \coprod }[/math] is frequently used, instead of [math]\displaystyle{ \bigsqcup, }[/math] to denote coproduct.
See also
- Coproduct – Category-theoretic construction
- Direct limit – Special case of colimit in category theory
- Disjoint union (topology)
- Disjoint union of graphs – Combining the vertex and edge sets of two graphs
- Intersection (set theory) – Set of elements common to all of some sets
- List of set identities and relations – Equalities for combinations of sets
- Partition of a set – Mathematical ways to group elements of a set
- Symmetric difference – Elements in exactly one of two sets
- Tagged union – Data structure used to hold a value that could take on several different, but fixed, types
References
- Lang, Serge (2004), Algebra, Graduate Texts in Mathematics, 211 (Corrected fourth printing, revised third ed.), New York: Springer-Verlag, p. 60, ISBN 978-0-387-95385-4
- Weisstein, Eric W.. "Disjoint Union". http://mathworld.wolfram.com/DisjointUnion.html.
 |

