Fuzzy relation
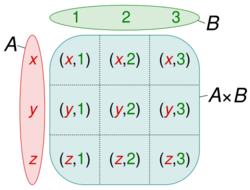
A fuzzy relation is the cartesian product of mathematical fuzzy sets.[1] Two fuzzy sets are taken as input, the fuzzy relation is then equal to the cross product of the sets which is created by vector multiplication. Usually, a rule base is stored in a matrix notation which allows the fuzzy controller to update its internal values.[2][3]
From a historical perspective, the first fuzzy relation was mentioned in the year 1971 by Lotfi A. Zadeh.[4]
A practical approach to describe a fuzzy relation is based on a 2d table. At first, a table is created which consists of fuzzy values from 0..1. The next step is to apply the if-then-rules to the values. The resulting numbers are stored in the table as an array.
Fuzzy relations can be utilized in fuzzy databases.[5]
References
- ↑ Timothy J. Ross (8 April 2005). Fuzzy Logic with Engineering Applications. John Wiley & Sons. pp. 59–. ISBN 978-0-470-86076-2. https://books.google.com/books?id=3zcgIKPl8L0C.
- ↑ Galindo, Jos (31 May 2008). Handbook of Research on Fuzzy Information Processing in Databases. IGI Global. pp. 17–. ISBN 978-1-59904-854-3. https://books.google.com/books?id=vaY9PTkrn3gC&pg=PA17.
- ↑ Witold Pedrycz (31 March 1996). Fuzzy Modelling: Paradigms and Practice. Springer Science & Business Media. pp. 39–. ISBN 978-0-7923-9703-8. https://books.google.com/books?id=31ngwZ8l-C0C&pg=PA39.
- ↑ Witold Pedrycz; Fernando Gomide (12 October 2007). Fuzzy Systems Engineering: Toward Human-Centric Computing. John Wiley & Sons. pp. 156–. ISBN 978-0-470-16895-0. https://books.google.com/books?id=VIFUBIMDqLsC&pg=PA156.
- ↑ Zongmin Ma (30 March 2006). Fuzzy Database Modeling with XML. Springer Science & Business Media. p. 97–. ISBN 978-0-387-24249-1. https://books.google.com/books?id=cR4ByFywfAUC.
 |
