Graph factorization

1-factorization of Desargues graph: each color class is a 1-factor.

Petersen graph can be partitioned into a 1-factor (red) and a 2-factor (blue). However, the graph is not 1-factorable.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.

1-factorization

If a graph is 1-factorable (i.e., has a 1-factorization), then it has to be a regular graph. However, not all regular graphs are 1-factorable. A k-regular graph is 1-factorable if it has chromatic index k; examples of such graphs include:

• Any regular bipartite graph. Hall's marriage theorem can be used to show that a k-regular bipartite graph contains a perfect matching. One can then remove the perfect matching to obtain a (k − 1)-regular bipartite graph, and apply the same reasoning repeatedly.
• Any complete graph with an even number of nodes (see below).

However, there are also k-regular graphs that have chromatic index k + 1, and these graphs are not 1-factorable; examples of such graphs include:

• Any regular graph with an odd number of nodes.
• The Petersen graph.

Complete graphs

1-factorization of K₈ in which each 1-factor consists of an edge from the center to a vertex of a heptagon together with all possible perpendicular edges

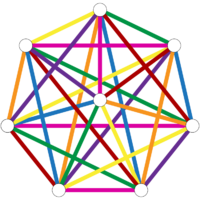
A 1-factorization of a complete graph corresponds to pairings in a round-robin tournament. The 1-factorization of complete graphs is a special case of Baranyai's theorem concerning the 1-factorization of complete hypergraphs.

One method for constructing a 1-factorization of a complete graph on an even number of vertices involves placing all but one of the vertices on a circle, forming a regular polygon, with the remaining vertex at the center of the circle. With this arrangement of vertices, one way of constructing a 1-factor of the graph is to choose an edge e from the center to a single polygon vertex together with all possible edges that lie on lines perpendicular to e. The 1-factors that can be constructed in this way form a 1-factorization of the graph.

The number of distinct 1-factorizations of K₂, K₄, K₆, K₈, ... is 1, 1, 6, 6240, 1225566720, 252282619805368320, 98758655816833727741338583040, ... OEIS: A000438.

1-factorization conjecture

Let G be a k-regular graph with 2n nodes. If k is sufficiently large, it is known that G has to be 1-factorable:

• If k = 2n − 1, then G is the complete graph K_2n, and hence 1-factorable (see above).
• If k = 2n − 2, then G can be constructed by removing a perfect matching from K_2n. Again, G is 1-factorable.
• (Chetwynd Hilton) show that if k ≥ 12n/7, then G is 1-factorable.

The 1-factorization conjecture is a long-standing conjecture that states that k ≈ n is sufficient. In precise terms, the conjecture is:

• If n is odd and k ≥ n, then G is 1-factorable. If n is even and k ≥ n − 1 then G is 1-factorable.

The overfull conjecture implies the 1-factorization conjecture.

Perfect 1-factorization

A perfect pair from a 1-factorization is a pair of 1-factors whose union induces a Hamiltonian cycle.

A perfect 1-factorization (P1F) of a graph is a 1-factorization having the property that every pair of 1-factors is a perfect pair. A perfect 1-factorization should not be confused with a perfect matching (also called a 1-factor).

In 1964, Anton Kotzig conjectured that every complete graph K_2n where n ≥ 2 has a perfect 1-factorization. So far, it is known that the following graphs have a perfect 1-factorization:

• the infinite family of complete graphs K_2p where p is an odd prime (by Anderson and also Nakamura, independently),
• the infinite family of complete graphs K_{p + 1} where p is an odd prime,
• and sporadic additional results, including K_2n where 2n ∈ {16, 28, 36, 40, 50, 126, 170, 244, 344, 730, 1332, 1370, 1850, 2198, 3126, 6860, 12168, 16808, 29792}. Some newer results are collected here.

If the complete graph K_{n + 1} has a perfect 1-factorization, then the complete bipartite graph K_n,n also has a perfect 1-factorization.

2-factorization

If a graph is 2-factorable, then it has to be 2k-regular for some integer k. Julius Petersen showed in 1891 that this necessary condition is also sufficient: any 2k-regular graph is 2-factorable.

If a connected graph is 2k-regular and has an even number of edges it may also be k-factored, by choosing each of the two factors to be an alternating subset of the edges of an Euler tour. This applies only to connected graphs; disconnected counterexamples include disjoint unions of odd cycles, or of copies of K_2k+1.

The Oberwolfach problem concerns the existence of 2-factorizations of complete graphs into isomorphic subgraphs. It asks for which subgraphs this is possible. This is known when the subgraph is connected (in which case it is a Hamiltonian cycle and this special case is the problem of Hamiltonian decomposition) but the general case remains unsolved.

Bibliography

• Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7, https://archive.org/details/graphtheorywitha0000bond, retrieved 2019-12-18 , Section 5.1: "Matchings".
• "Regular graphs of high degree are 1-factorizable", Proceedings of the London Mathematical Society 50 (2): 193–206, 1985, doi:10.1112/plms/s3-50.2.193 .
• Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6 , Chapter 2: "Matching, covering and packing". Electronic edition.
• Graph Theory, Addison-Wesley, 1969, ISBN 0-201-02787-9 , Chapter 9: "Factorization".
• Hazewinkel, Michiel, ed. (2001), "One-factorization", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/o110070 
• Niessen, Thomas (1994), "How to find overfull subgraphs in graphs with large maximum degree", Discrete Applied Mathematics 51 (1–2): 117–125, doi:10.1016/0166-218X(94)90101-5 .
• Perkovic, L. (1997), "Edge coloring regular graphs of high degree", Discrete Mathematics 165–166: 567–578, doi:10.1016/S0012-365X(96)00202-6 .
• "Die Theorie der regulären graphs", Acta Mathematica 15: 193–220, 1891, doi:10.1007/BF02392606 .
• West, Douglas B.. "1-Factorization Conjecture (1985?)". Open Problems – Graph Theory and Combinatorics. http://www.math.uiuc.edu/~west/openp/1fact.html. 
• Weisstein, Eric W.. "Graph Factor". http://mathworld.wolfram.com/GraphFactor.html. 
• Weisstein, Eric W.. "k-Factor". http://mathworld.wolfram.com/k-Factor.html. 
• Weisstein, Eric W.. "k-Factorable Graph". http://mathworld.wolfram.com/k-FactorableGraph.html. 

Further reading

• "Graph factors and factorization: 1985–2003: A survey", Discrete Mathematics 307 (7–8): 791–821, 2007, doi:10.1016/j.disc.2005.11.059 .