Hemicontinuity

In mathematics, the notion of the continuity of functions is not immediately extensible to set-valued functions between two sets A and B. The dual concepts of upper hemicontinuity and lower hemicontinuity facilitate such an extension. A set-valued function that has both properties is said to be continuous in an analogy to the property of the same name for single-valued functions.

To explain both notions, consider a sequence a of points in a domain, and a sequence b of points in the range. We say that b corresponds to a if each point in b is contained in the image of the corresponding point in a.

• Upper hemicontinuity requires that, for any convergent sequence a in a domain, and for any convergent sequence b that corresponds to a, the image of the limit of a contains the limit of b.
• Lower hemicontinuity requires that, for any convergent sequence a in a domain, and for any point x in the image of the limit of a, there exists a sequence b that corresponds to a subsequence of a, that converges to x.

Examples

This set-valued function is upper hemicontinuous everywhere, but not lower hemicontinuous at [math]\displaystyle{ x }[/math] : for a sequence of points [math]\displaystyle{ \left(x_m\right) }[/math] that converges to [math]\displaystyle{ x, }[/math] we have a [math]\displaystyle{ y }[/math] ([math]\displaystyle{ y \in f(x) }[/math]) such that no sequence of [math]\displaystyle{ \left(y_m\right) }[/math] converges to [math]\displaystyle{ y }[/math] where each [math]\displaystyle{ y_m }[/math] is in [math]\displaystyle{ f\left(x_m\right). }[/math]

This set-valued function is lower hemicontinuous everywhere, but not upper hemicontinuous at [math]\displaystyle{ x, }[/math] because the graph (set) is not closed.

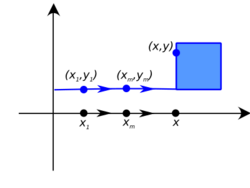
The image on the right shows a function that is not lower hemicontinuous at x. To see this, let a be a sequence that converges to x from the left. The image of x is a vertical line that contains some point (x,y). But every sequence b that corresponds to a is contained in the bottom horizontal line, so it cannot converge to y. In contrast, the function is upper hemicontinuous everywhere. For example, considering any sequence a that converges to x from the left or from the right, and any corresponding sequence b, the limit of b is contained in the vertical line that is the image of the limit of a.

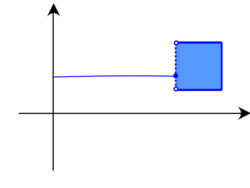
The image on the left shows a function that is not upper hemicontinuous at x. To see this, let a be a sequence that converges to x from the right. The image of a contains vertical lines, so there exists a corresponding sequence b in which all elements are bounded away from f(x). The image of the limit of a contains a single point f(x), so it does not contain the limit of b. In contrast, that function is lower hemicontinuous everywhere. For example, for any sequence a that converges to x, from the left or from the right, f(x) contains a single point, and there exists a corresponding sequence b that converges to f(x).

Formal definition: upper hemicontinuity

A set-valued function [math]\displaystyle{ \Gamma : A \to B }[/math] is said to be upper hemicontinuous at the point [math]\displaystyle{ a }[/math] if, for any open [math]\displaystyle{ V \subset B }[/math] with [math]\displaystyle{ \Gamma(a) \subset V }[/math], there exists a neighbourhood [math]\displaystyle{ U }[/math] of [math]\displaystyle{ a }[/math] such that for all [math]\displaystyle{ x \in U, }[/math] [math]\displaystyle{ \Gamma(x) }[/math] is a subset of [math]\displaystyle{ V. }[/math]

Sequential characterization

For a set-valued function [math]\displaystyle{ \Gamma : A \to B }[/math] with closed values, if [math]\displaystyle{ \Gamma : A \to B }[/math] is upper hemicontinuous at [math]\displaystyle{ a \in A }[/math] then for all sequences [math]\displaystyle{ a_{\bull} = \left(a_m\right)_{m=1}^{\infty} }[/math] in [math]\displaystyle{ A }[/math] and all sequences [math]\displaystyle{ \left(b_m\right)_{m=1}^{\infty} }[/math] such that [math]\displaystyle{ b_m \in \Gamma\left(a_m\right), }[/math]

if [math]\displaystyle{ \lim_{m \to \infty} a_m = a }[/math] and [math]\displaystyle{ \lim_{m \to \infty} b_m = b }[/math] then [math]\displaystyle{ b \in \Gamma(a). }[/math]

As an example, look at the image at the right, and consider sequence a in the domain that converges to x (either from the left or from the right). Then, any sequence b that satisfies the requirements converges to some point in f(x). Therefore, the

If B is compact, the converse is also true.

Closed graph theorem

The graph of a set-valued function [math]\displaystyle{ \Gamma : A \to B }[/math] is the set defined by [math]\displaystyle{ Gr(\Gamma) = \{ (a,b) \in A \times B : b \in \Gamma(a) \}. }[/math]

If [math]\displaystyle{ \Gamma : A \to B }[/math] is an upper hemicontinuous set-valued function with closed domain (that is, the set of points [math]\displaystyle{ a \in A }[/math] where [math]\displaystyle{ \Gamma(a) }[/math] is not the empty set is closed) and closed values (i.e. [math]\displaystyle{ \Gamma(a) }[/math] is closed for all [math]\displaystyle{ a \in A }[/math]), then [math]\displaystyle{ \operatorname{Gr}(\Gamma) }[/math] is closed. If [math]\displaystyle{ B }[/math] is compact, then the converse is also true.

Formal definition: lower hemicontinuity

A set-valued function [math]\displaystyle{ \Gamma : A \to B }[/math] is said to be lower hemicontinuous at the point [math]\displaystyle{ a }[/math] if for any open set [math]\displaystyle{ V }[/math] intersecting [math]\displaystyle{ \Gamma(a) }[/math] there exists a neighbourhood [math]\displaystyle{ U }[/math] of [math]\displaystyle{ a }[/math] such that [math]\displaystyle{ \Gamma(x) }[/math] intersects [math]\displaystyle{ V }[/math] for all [math]\displaystyle{ x \in U. }[/math] (Here [math]\displaystyle{ V }[/math] intersects [math]\displaystyle{ S }[/math] means nonempty intersection [math]\displaystyle{ V \cap S \neq \varnothing }[/math]).

Sequential characterization

[math]\displaystyle{ \Gamma : A \to B }[/math] is lower hemicontinuous at [math]\displaystyle{ a }[/math] if and only if for every sequence [math]\displaystyle{ a_{\bull} = \left(a_m\right)_{m=1}^{\infty} }[/math] in [math]\displaystyle{ A }[/math] such that [math]\displaystyle{ a_{\bull} \to a }[/math] in [math]\displaystyle{ A }[/math] and all [math]\displaystyle{ b \in \Gamma(a), }[/math] there exists a subsequence [math]\displaystyle{ \left(a_{m_k}\right)_{k=1}^{\infty} }[/math] of [math]\displaystyle{ a_{\bull} }[/math] and also a sequence [math]\displaystyle{ b_{\bull} = \left(b_k\right)_{k=1}^{\infty} }[/math] such that [math]\displaystyle{ b_{\bull} \to b }[/math] and [math]\displaystyle{ b_k \in \Gamma\left(a_{m_k}\right) }[/math] for every [math]\displaystyle{ k. }[/math]

Open graph theorem

A set-valued function [math]\displaystyle{ \Gamma : A \to B }[/math] have open lower sections if the set [math]\displaystyle{ \Gamma^{-1}(b) = \{ a \in A : b \in \Gamma(a) \} }[/math] is open in [math]\displaystyle{ A }[/math] for every [math]\displaystyle{ b \in B. }[/math] If [math]\displaystyle{ \Gamma }[/math] values are all open sets in [math]\displaystyle{ B, }[/math] then [math]\displaystyle{ \Gamma }[/math] is said to have open upper sections.

If [math]\displaystyle{ \Gamma }[/math] has an open graph [math]\displaystyle{ \operatorname{Gr}(\Gamma), }[/math] then [math]\displaystyle{ \Gamma }[/math] has open upper and lower sections and if [math]\displaystyle{ \Gamma }[/math] has open lower sections then it is lower hemicontinuous.

The open graph theorem says that if [math]\displaystyle{ \Gamma : A \to P\left(\R^n\right) }[/math] is a set-valued function with convex values and open upper sections, then [math]\displaystyle{ \Gamma }[/math] has an open graph in [math]\displaystyle{ A \times \R^n }[/math] if and only if [math]\displaystyle{ \Gamma }[/math] is lower hemicontinuous.

Properties

Set-theoretic, algebraic and topological operations on set-valued functions (like union, composition, sum, convex hull, closure) usually preserve the type of continuity. But this should be taken with appropriate care since, for example, there exists a pair of lower hemicontinuous set-valued functions whose intersection is not lower hemicontinuous. This can be fixed upon strengthening continuity properties: if one of those lower hemicontinuous multifunctions has open graph then their intersection is again lower hemicontinuous.

Crucial to set-valued analysis (in view of applications) are the investigation of single-valued selections and approximations to set-valued functions. Typically lower hemicontinuous set-valued functions admit single-valued selections (Michael selection theorem, Bressan–Colombo directionally continuous selection theorem, Fryszkowski decomposable map selection). Likewise, upper hemicontinuous maps admit approximations (e.g. Ancel–Granas–Górniewicz–Kryszewski theorem).

Implications for continuity

If a set-valued function is both upper hemicontinuous and lower hemicontinuous, it is said to be continuous. A continuous function is in all cases both upper and lower hemicontinuous.

Other concepts of continuity

The upper and lower hemicontinuity might be viewed as usual continuity:

[math]\displaystyle{ \Gamma : A \to B }[/math] is lower [resp. upper] hemicontinuous if and only if the mapping [math]\displaystyle{ \Gamma : A \to P(B) }[/math] is continuous where the hyperspace P(B) has been endowed with the lower [resp. upper] Vietoris topology.

(For the notion of hyperspace compare also power set and function space).

Using lower and upper Hausdorff uniformity we can also define the so-called upper and lower semicontinuous maps in the sense of Hausdorff (also known as metrically lower / upper semicontinuous maps).

See also

• Differential inclusion
• Hausdorff distance – Distance between two metric-space subsets

References

• Template:Aliprantis Border Infinite Dimensional Analysis A Hitchhiker's Guide Third Edition
• Aubin, Jean-Pierre; Cellina, Arrigo (1984). Differential Inclusions: Set-Valued Maps and Viability Theory. Grundl. der Math. Wiss.. 264. Berlin: Springer. ISBN 0-387-13105-1. https://books.google.com/books?id=rVnsCAAAQBAJ. 
• Aubin, Jean-Pierre; Frankowska, Hélène (1990). Set-Valued Analysis. Basel: Birkhäuser. ISBN 3-7643-3478-9. https://books.google.com/books?id=cVUl3smcGlcC. 
• Deimling, Klaus (1992). Multivalued Differential Equations. Walter de Gruyter. ISBN 3-11-013212-5. https://books.google.com/books?id=ejhT-QMEVZ0C. 
• Mas-Colell, Andreu; Whinston, Michael D.; Green, Jerry R. (1995). Microeconomic Analysis. New York: Oxford University Press. pp. 949–951. ISBN 0-19-507340-1. https://books.google.com/books?id=KGtegVXqD8wC&pg=PA949. 
• Ok, Efe A. (2007). Real Analysis with Economic Applications. Princeton University Press. pp. 216–226. ISBN 978-0-691-11768-3.