Hexagonal fast Fourier transform

The fast Fourier transform (FFT) is an important tool in the fields of image and signal processing. The hexagonal fast Fourier transform (HFFT) uses existing FFT routines to compute the discrete Fourier transform (DFT) of images that have been captured with hexagonal sampling. The hexagonal grid serves as the optimal sampling lattice for isotropically band-limited two-dimensional signals and has a sampling efficiency which is 13.4% greater than the sampling efficiency obtained from rectangular sampling. Several other advantages of hexagonal sampling include consistent connectivity, higher symmetry, greater angular resolution, and equidistant neighbouring pixels. Sometimes, more than one of these advantages compound together, thereby increasing the efficiency by 50% in terms of computation and storage when compared to rectangular sampling. Despite all of these advantages of hexagonal sampling over rectangular sampling, its application has been limited because of the lack of an efficient coordinate system. However that limitation has been removed with the recent development of the hexagonal efficient coordinate system (HECS, formerly known as array set addressing or ASA) which includes the benefit of a separable Fourier kernel. The existence of a separable Fourier kernel for a hexagonally sampled image allows the use of existing FFT routines to efficiently compute the DFT of such an image.

Preliminaries

Hexagonal Efficient Coordinate System (HECS)

Representation of hexagonally sampled data as a pair of rectangular arrays using the HECS coordinate system

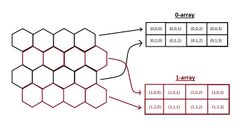
The hexagonal efficient coordinate system (formerly known as array set addressing (ASA)) was developed based on the fact that a hexagonal grid can be represented as a combination of two interleaved rectangular arrays. It is easy to address each individual array using familiar integer-valued row and column indices and the individual arrays are distinguished by a single binary coordinate. Therefore, a full address for any point in the hexagonal grid can be uniquely represented by three coordinates.

[math]\displaystyle{ (a,r,c) \in \{ 0,1 \} \times\mathbb Z \times\mathbb Z }[/math]

where the coordinates a, r and c represent the array, row and column respectively. The figure shows how the hexagonal grid is represented by two interleaved rectangular arrays in HECS coordinates.

Hexagonal discrete Fourier transform

The hexagonal discrete Fourier transform (HDFT) has been developed by Mersereau and it has been converted to an HECS representation by Rummelt. Let [math]\displaystyle{ x(a, r, c) }[/math] be a two-dimensional hexagonally sampled signal and let both arrays be of size [math]\displaystyle{ n\times m }[/math]. Let, [math]\displaystyle{ X(b, s, d) }[/math] be the Fourier transform of x. The HDFT equation for the forward transform as shown in is given by

[math]\displaystyle{ X(b, s, d) = \sum_a \sum_r \sum_c x(a, r, c)E(\cdot) }[/math]

where

[math]\displaystyle{ E(\cdot) = \exp\left[-j\pi\left(\frac{(a+2c)(b+2d)}{2m} + \frac{(a+2r)(b+2s)}{n}\right)\right] }[/math]

Note that the above equation is separable and hence can be expressed as

[math]\displaystyle{ X(b, s, d) = f_0(b, s, d) + W(\cdot) f_1(b, s, d) }[/math]

where

[math]\displaystyle{ W(\cdot) = \exp\left[-j\pi\left(\frac{b+2d}{2m} + \frac{b+2s}{n}\right)\right] }[/math]

and

[math]\displaystyle{ g_a(b, r, d) = \sum_c x(a, r, c) \exp\left(-j2\pi \frac{(c)(b+2d)}{2m} \right) }[/math]

[math]\displaystyle{ f_a(b, s, d) = \sum_r g_a(b, r, d) \exp\left(-j2\pi\frac{(r)(b+2s)}{n}\right) }[/math]

Hexagonal fast Fourier transform (HFFT)

The linear transforms [math]\displaystyle{ g_a }[/math] and [math]\displaystyle{ f_{a} }[/math] are similar to the rectangular Fourier kernel where a linear transform is applied along each dimension of the 2-D rectangular data. Note that each of these equations, discussed above, is a combination of four rectangular arrays that serve as precursors to the HDFT. Two, out of those four rectangular [math]\displaystyle{ g_{a} }[/math] terms contribute to the sub-array of HFFT. Now, by switching the binary coordinate, we have four different forms of equations. In, the three out of those four expressions have been evaluated using what the author called "non-standard transforms (NSTs)" (shown below) while one expression is computed using any correct and applicable FFT algorithm.

[math]\displaystyle{ g_a(0, r, d) = \sum_c x(a, r, c) \exp\left( -j2\pi \frac{(c)(d)}{m} \right) }[/math]

[math]\displaystyle{ g_a(1, r, d) = \sum_c x(a, r, c) \exp\left(-j2\pi \frac{(c)(2d+1)}{2m} \right) }[/math]

[math]\displaystyle{ f_a(0, s, d) = \sum_r g_{a}(a, r, d) \exp\left(-j2\pi \frac{(r)(2s)}{n}\right) }[/math]

[math]\displaystyle{ f_a(1, s, d) = \sum_r g_{a}(a, r, d) \exp\left(-j2\pi \frac{(r)(2s+1)}{n}\right) }[/math]

Looking at the second expression, [math]\displaystyle{ g_{a}(1,r,d) }[/math], we see that it is nothing more than a standard discrete Fourier transform (DFT) with a constant offset along the rows of rectangular sub-arrays of a hexagonally-sampled image [math]\displaystyle{ x(a, r, c) }[/math]. This expression is nothing more than a circular rotation of the DFT. Note that the shift must happen in the integer number of samples for the property to hold. This way, the function [math]\displaystyle{ g_{a} }[/math] can be computed using the standard DFT, in same number of operations, without introducing an NST.

If we have a look at 0-array [math]\displaystyle{ f_{a} }[/math], the expression will always be symmetric about half its spatial period. Because of this, it is enough to compute only half of it. We find that this expression is the standard DFT of the columns of [math]\displaystyle{ g_{a} }[/math], which is decimated by a factor of 2 and then is duplicated to span the space of r for the identical second period of the complex exponential. Mathematically,

[math]\displaystyle{ \begin{align} X_\text{even}[k] & = \sum_{n=0}^{N-1} x[n]e^{-\tfrac{2j\pi}{N}2kn} \\[5pt] & = \sum_{n=0}^{\tfrac{N}{2}-1} x[n]e^{-\tfrac{2j\pi}{N/2}kn} + \sum_{n=\tfrac{N}{2}}^{N-1} x[n]e^{-\tfrac{2j\pi}{N/2}kn} \\[5pt] & = \sum_{n=0}^{\tfrac{N}{2}-1} x[n]e^{-\tfrac{2j\pi}{N/2}kn} + \sum_{n=0}^{\tfrac{N}{2}-1} x\left[n+\tfrac{N}{2}\right]e^{-\tfrac{2j\pi}{N/2}kn} \\[5pt] & = \sum_{n=0}^{\tfrac{N}{2}-1} \left(x[n]+x\left[n+\tfrac{N}{2}\right]\right)e^{-\tfrac{2j\pi}{N/2}kn} \end{align} }[/math]

The expression for the 1-array [math]\displaystyle{ f_a }[/math] is equivalent to the 0-array expression with a shift of one sample. Hence, the 1-array expression can be expressed as columns of the DFT of [math]\displaystyle{ g_{a} }[/math] decimated by a factor of two, starting with second sample providing a constant offset needed by 1-array, and then doubled in space to span the range of s. Thus, the method developed by James B. Birdsong and Nicholas I. Rummelt in is able to successfully compute the HFFT using the standard FFT routines unlike the previous work in.