Jensen's inequality

Short description: Theorem of convex functions

Jensen's inequality generalizes the statement that a secant line of a convex function lies above its graph.

File:Convex 01.ogg

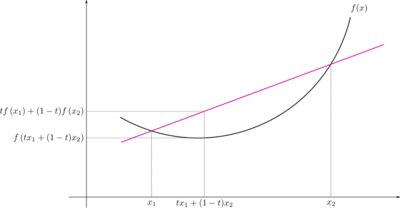
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations.

Jensen's inequality generalizes the statement that the secant line of a convex function lies above the graph of the function, which is Jensen's inequality for two points: the secant line consists of weighted means of the convex function (for t ∈ [0,1]),

[math]\displaystyle{ t f(x_1) + (1-t) f(x_2), }[/math]

while the graph of the function is the convex function of the weighted means,

[math]\displaystyle{ f(t x_1 + (1-t) x_2). }[/math]

Thus, Jensen's inequality is

[math]\displaystyle{ f(t x_1 + (1-t) x_2) \leq t f(x_1) + (1-t) f(x_2). }[/math]

In the context of probability theory, it is generally stated in the following form: if X is a random variable and φ is a convex function, then

[math]\displaystyle{ \varphi(\operatorname{E}[X]) \leq \operatorname{E} \left[\varphi(X)\right]. }[/math]

The difference between the two sides of the inequality, [math]\displaystyle{ \operatorname{E} \left[\varphi(X)\right] - \varphi\left(\operatorname{E}[X]\right) }[/math], is called the Jensen gap.

Statements

The classical form of Jensen's inequality involves several numbers and weights. The inequality can be stated quite generally using either the language of measure theory or (equivalently) probability. In the probabilistic setting, the inequality can be further generalized to its full strength.

Finite form

For a real convex function [math]\displaystyle{ \varphi }[/math], numbers [math]\displaystyle{ x_1, x_2, \ldots, x_n }[/math] in its domain, and positive weights [math]\displaystyle{ a_i }[/math], Jensen's inequality can be stated as:

[math]\displaystyle{ \varphi\left(\frac{\sum a_i x_i}{\sum a_i}\right) \le \frac{\sum a_i \varphi (x_i)}{\sum a_i} }[/math]

(1)

and the inequality is reversed if [math]\displaystyle{ \varphi }[/math] is concave, which is

[math]\displaystyle{ \varphi\left(\frac{\sum a_i x_i}{\sum a_i}\right) \geq \frac{\sum a_i \varphi (x_i)}{\sum a_i}. }[/math]

(2)

Equality holds if and only if [math]\displaystyle{ x_1=x_2=\cdots =x_n }[/math] or [math]\displaystyle{ \varphi }[/math] is linear on a domain containing [math]\displaystyle{ x_1,x_2,\cdots ,x_n }[/math].

As a particular case, if the weights [math]\displaystyle{ a_i }[/math] are all equal, then (1) and (2) become

[math]\displaystyle{ \varphi\left(\frac{\sum x_i}{n}\right) \le \frac{\sum \varphi (x_i)}{n} }[/math]

(3)

[math]\displaystyle{ \varphi\left(\frac{\sum x_i}{n}\right) \geq \frac{\sum \varphi (x_i)}{n} }[/math]

(4)

For instance, the function log(x) is concave, so substituting [math]\displaystyle{ \varphi(x) = \log(x) }[/math] in the previous formula (4) establishes the (logarithm of the) familiar arithmetic-mean/geometric-mean inequality:

[math]\displaystyle{ \log\!\left( \frac{\sum_{i=1}^n x_i}{n}\right) \geq \frac{\sum_{i=1}^n \log\!\left( x_i \right)}{n} \quad \text{or} \quad \frac{x_1 + x_2 + \cdots + x_n}{n} \geq \sqrt[n]{x_1 \cdot x_2 \cdots x_n} }[/math]

A common application has x as a function of another variable (or set of variables) t, that is, [math]\displaystyle{ x_i = g(t_i) }[/math]. All of this carries directly over to the general continuous case: the weights a_i are replaced by a non-negative integrable function  f (x), such as a probability distribution, and the summations are replaced by integrals.

Measure-theoretic form

Let [math]\displaystyle{ (\Omega, A, \mu) }[/math] be a probability space. Let [math]\displaystyle{ f : \Omega \to \mathbb{R} }[/math] be a [math]\displaystyle{ \mu }[/math]-measurable function and [math]\displaystyle{ \varphi : \mathbb{R} \to \mathbb{R} }[/math] be convex. Then: [math]\displaystyle{ \varphi\left(\int_\Omega f \,\mathrm{d}\mu\right) \leq \int_\Omega \varphi \circ f \,\mathrm{d}\mu }[/math]

In real analysis, we may require an estimate on

[math]\displaystyle{ \varphi\left(\int_a^b f(x)\, dx\right) }[/math]

where [math]\displaystyle{ a, b \in \mathbb{R} }[/math], and [math]\displaystyle{ f\colon[a, b] \to \R }[/math] is a non-negative Lebesgue-integrable function. In this case, the Lebesgue measure of [math]\displaystyle{ [a, b] }[/math] need not be unity. However, by integration by substitution, the interval can be rescaled so that it has measure unity. Then Jensen's inequality can be applied to get

[math]\displaystyle{ \varphi\left(\frac{1}{b-a}\int_a^b f(x)\, dx\right) \le \frac{1}{b-a} \int_a^b \varphi(f(x)) \,dx. }[/math]

Probabilistic form

The same result can be equivalently stated in a probability theory setting, by a simple change of notation. Let [math]\displaystyle{ (\Omega, \mathfrak{F},\operatorname{P}) }[/math] be a probability space, X an integrable real-valued random variable and φ a convex function. Then:

[math]\displaystyle{ \varphi\left(\operatorname{E}[X]\right) \leq \operatorname{E} \left[ \varphi(X) \right]. }[/math]

In this probability setting, the measure μ is intended as a probability [math]\displaystyle{ \operatorname{P} }[/math], the integral with respect to μ as an expected value [math]\displaystyle{ \operatorname{E} }[/math], and the function [math]\displaystyle{ f }[/math] as a random variable X.

Note that the equality holds if and only if φ is a linear function on some convex set [math]\displaystyle{ A }[/math] such that [math]\displaystyle{ \mathrm{P}(X \in A) = 1 }[/math] (which follows by inspecting the measure-theoretical proof below).

General inequality in a probabilistic setting

More generally, let T be a real topological vector space, and X a T-valued integrable random variable. In this general setting, integrable means that there exists an element [math]\displaystyle{ \operatorname{E}[X] }[/math] in T, such that for any element z in the dual space of T: [math]\displaystyle{ \operatorname{E}|\langle z, X \rangle|\lt \infty }[/math], and [math]\displaystyle{ \langle z, \operatorname{E}[X]\rangle = \operatorname{E}[\langle z, X \rangle] }[/math]. Then, for any measurable convex function φ and any sub-σ-algebra [math]\displaystyle{ \mathfrak{G} }[/math] of [math]\displaystyle{ \mathfrak{F} }[/math]:

[math]\displaystyle{ \varphi\left(\operatorname{E}\left[X\mid\mathfrak{G}\right]\right) \leq \operatorname{E}\left[\varphi(X)\mid\mathfrak{G}\right]. }[/math]

Here [math]\displaystyle{ \operatorname{E}[\cdot\mid\mathfrak{G}] }[/math] stands for the expectation conditioned to the σ-algebra [math]\displaystyle{ \mathfrak{G} }[/math]. This general statement reduces to the previous ones when the topological vector space T is the real axis, and [math]\displaystyle{ \mathfrak{G} }[/math] is the trivial σ-algebra {∅, Ω} (where ∅ is the empty set, and Ω is the sample space).

A sharpened and generalized form

Let X be a one-dimensional random variable with mean [math]\displaystyle{ \mu }[/math] and variance [math]\displaystyle{ \sigma^2\ge 0 }[/math]. Let [math]\displaystyle{ \varphi(x) }[/math] be a twice differentiable function, and define the function

[math]\displaystyle{ h(x)\triangleq\frac{\varphi \left(x\right)-\varphi \left(\mu \right)}{\left(x-\mu \right)^2}-\frac{\varphi '\left(\mu \right)}{x-\mu}. }[/math]

Then

[math]\displaystyle{ \sigma^2\inf \frac{\varphi''(x)}{2} \le \sigma^2\inf h(x) \leq E\left[\varphi \left(X\right)\right]-\varphi\left(E[X]\right)\le \sigma^2\sup h(x) \le \sigma^2\sup \frac{\varphi''(x)}{2}. }[/math]

In particular, when [math]\displaystyle{ \varphi(x) }[/math] is convex, then [math]\displaystyle{ \varphi''(x)\ge 0 }[/math], and the standard form of Jensen's inequality immediately follows for the case where [math]\displaystyle{ \varphi(x) }[/math] is additionally assumed to be twice differentiable.

Proofs

Intuitive graphical proof

A graphical "proof" of Jensen's inequality for the probabilistic case. The dashed curve along the X axis is the hypothetical distribution of X, while the dashed curve along the Y axis is the corresponding distribution of Y values. Note that the convex mapping Y(X) increasingly "stretches" the distribution for increasing values of X.

This is a proof without words of Jensen's inequality for n variables. Without loss of generality, the sum of the positive weights is 1. It follows that the weighted point lies in the convex hull of the original points, which lies above the function itself by the definition of convexity. The conclusion follows.

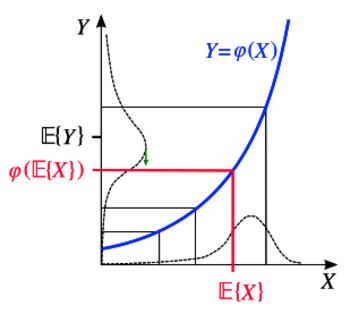
Jensen's inequality can be proved in several ways, and three different proofs corresponding to the different statements above will be offered. Before embarking on these mathematical derivations, however, it is worth analyzing an intuitive graphical argument based on the probabilistic case where X is a real number (see figure). Assuming a hypothetical distribution of X values, one can immediately identify the position of [math]\displaystyle{ \operatorname{E}[X] }[/math] and its image [math]\displaystyle{ \varphi(\operatorname{E}[X]) }[/math] in the graph. Noticing that for convex mappings Y = φ(x) of some x values the corresponding distribution of Y values is increasingly "stretched up" for increasing values of X, it is easy to see that the distribution of Y is broader in the interval corresponding to X > X₀ and narrower in X < X₀ for any X₀; in particular, this is also true for [math]\displaystyle{ X_0 = \operatorname{E}[X] }[/math]. Consequently, in this picture the expectation of Y will always shift upwards with respect to the position of [math]\displaystyle{ \varphi(\operatorname{E}[X]) }[/math]. A similar reasoning holds if the distribution of X covers a decreasing portion of the convex function, or both a decreasing and an increasing portion of it. This "proves" the inequality, i.e.

[math]\displaystyle{ \varphi(\operatorname{E}[X]) \leq \operatorname{E}[\varphi(X)] = \operatorname{E}[Y], }[/math]

with equality when φ(X) is not strictly convex, e.g. when it is a straight line, or when X follows a degenerate distribution (i.e. is a constant).

The proofs below formalize this intuitive notion.

Proof 1 (finite form)

If λ₁ and λ₂ are two arbitrary nonnegative real numbers such that λ₁ + λ₂ = 1 then convexity of φ implies

[math]\displaystyle{ \forall x_1, x_2: \qquad \varphi \left (\lambda_1 x_1+\lambda_2 x_2 \right )\leq \lambda_1\,\varphi(x_1)+\lambda_2\,\varphi(x_2). }[/math]

This can be generalized: if λ₁, ..., λ_n are nonnegative real numbers such that λ₁ + ... + λ_n = 1, then

[math]\displaystyle{ \varphi(\lambda_1 x_1+\lambda_2 x_2+\cdots+\lambda_n x_n)\leq \lambda_1\,\varphi(x_1)+\lambda_2\,\varphi(x_2)+\cdots+\lambda_n\,\varphi(x_n), }[/math]

for any x₁, ..., x_n.

The finite form of the Jensen's inequality can be proved by induction: by convexity hypotheses, the statement is true for n = 2. Suppose the statement is true for some n, so

[math]\displaystyle{ \varphi\left(\sum_{i=1}^{n}\lambda_i x_i\right) \leq \sum_{i=1}^{n}\lambda_i \varphi\left(x_i\right) }[/math]

for any λ₁, ..., λ_n such that λ₁ + ... + λ_n = 1.

One needs to prove it for n + 1. At least one of the λ_i is strictly smaller than [math]\displaystyle{ 1 }[/math], say λ_n+1; therefore by convexity inequality:

[math]\displaystyle{ \begin{align} \varphi\left(\sum_{i=1}^{n+1}\lambda_i x_i\right) &= \varphi\left((1-\lambda_{n+1})\sum_{i=1}^{n} \frac{\lambda_i}{1-\lambda_{n+1}} x_i + \lambda_{n+1} x_{n+1} \right) \\ &\leq (1-\lambda_{n+1}) \varphi\left(\sum_{i=1}^{n} \frac{\lambda_i}{1-\lambda_{n+1}} x_i \right)+\lambda_{n+1}\,\varphi(x_{n+1}). \end{align} }[/math]

Since λ₁ + ... +λ_n + λ_n+1 = 1,

[math]\displaystyle{ \sum_{i=1}^{n} \frac{\lambda_i}{1-\lambda_{n+1}} = 1 }[/math],

applying the inductive hypothesis gives

[math]\displaystyle{ \varphi\left(\sum_{i=1}^{n}\frac{\lambda_i}{1-\lambda_{n+1}} x_i\right) \leq \sum_{i=1}^{n}\frac{\lambda_i}{1-\lambda_{n+1}} \varphi(x_i) }[/math]

therefore

[math]\displaystyle{ \begin{align} \varphi\left(\sum_{i=1}^{n+1}\lambda_i x_i\right) &\leq (1-\lambda_{n+1}) \sum_{i=1}^{n}\frac{\lambda_i}{1-\lambda_{n+1}} \varphi(x_i)+\lambda_{n+1}\,\varphi(x_{n+1}) =\sum_{i=1}^{n+1}\lambda_i \varphi(x_i) \end{align} }[/math]

We deduce the equality is true for n + 1, by induction it follows that the result is also true for all integer n greater than 2.

In order to obtain the general inequality from this finite form, one needs to use a density argument. The finite form can be rewritten as:

[math]\displaystyle{ \varphi\left(\int x\,d\mu_n(x) \right)\leq \int \varphi(x)\,d\mu_n(x), }[/math]

where μ_n is a measure given by an arbitrary convex combination of Dirac deltas:

[math]\displaystyle{ \mu_n= \sum_{i=1}^n \lambda_i \delta_{x_i}. }[/math]

Since convex functions are continuous, and since convex combinations of Dirac deltas are weakly dense in the set of probability measures (as could be easily verified), the general statement is obtained simply by a limiting procedure.

Proof 2 (measure-theoretic form)

Let [math]\displaystyle{ g }[/math] be a real-valued [math]\displaystyle{ \mu }[/math]-integrable function on a probability space [math]\displaystyle{ \Omega }[/math], and let [math]\displaystyle{ \varphi }[/math] be a convex function on the real numbers. Since [math]\displaystyle{ \varphi }[/math] is convex, at each real number [math]\displaystyle{ x }[/math] we have a nonempty set of subderivatives, which may be thought of as lines touching the graph of [math]\displaystyle{ \varphi }[/math] at [math]\displaystyle{ x }[/math], but which are below the graph of [math]\displaystyle{ \varphi }[/math] at all points (support lines of the graph).

Now, if we define

[math]\displaystyle{ x_0:=\int_\Omega g\, d\mu, }[/math]

because of the existence of subderivatives for convex functions, we may choose [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] such that

[math]\displaystyle{ ax + b \leq \varphi(x), }[/math]

for all real [math]\displaystyle{ x }[/math] and

[math]\displaystyle{ ax_0+ b = \varphi(x_0). }[/math]

But then we have that

[math]\displaystyle{ \varphi \circ g (\omega) \geq ag(\omega)+ b }[/math]

for almost all [math]\displaystyle{ \omega \in \Omega }[/math]. Since we have a probability measure, the integral is monotone with [math]\displaystyle{ \mu(\Omega) = 1 }[/math] so that

[math]\displaystyle{ \int_\Omega \varphi \circ g\, d\mu \geq \int_\Omega (ag + b)\, d\mu = a\int_\Omega g\, d\mu + b\int_\Omega d\mu = ax_0 + b = \varphi (x_0) = \varphi \left (\int_\Omega g\, d\mu \right ), }[/math]

as desired.

Proof 3 (general inequality in a probabilistic setting)

Let X be an integrable random variable that takes values in a real topological vector space T. Since [math]\displaystyle{ \varphi: T \to \R }[/math] is convex, for any [math]\displaystyle{ x,y \in T }[/math], the quantity

[math]\displaystyle{ \frac{\varphi(x+\theta\,y)-\varphi(x)}{\theta}, }[/math]

is decreasing as θ approaches 0⁺. In particular, the subdifferential of [math]\displaystyle{ \varphi }[/math] evaluated at x in the direction y is well-defined by

[math]\displaystyle{ (D\varphi)(x)\cdot y:=\lim_{\theta \downarrow 0} \frac{\varphi(x+\theta\,y)-\varphi(x)}{\theta}=\inf_{\theta \neq 0} \frac{\varphi(x+\theta\,y)-\varphi(x)}{\theta}. }[/math]

It is easily seen that the subdifferential is linear in y (that is false and the assertion requires Hahn-Banach theorem to be proved) and, since the infimum taken in the right-hand side of the previous formula is smaller than the value of the same term for θ = 1, one gets

[math]\displaystyle{ \varphi(x)\leq \varphi(x+y)-(D\varphi)(x)\cdot y. }[/math]

In particular, for an arbitrary sub-σ-algebra [math]\displaystyle{ \mathfrak{G} }[/math] we can evaluate the last inequality when [math]\displaystyle{ x = \operatorname{E}[X\mid\mathfrak{G}],\,y=X-\operatorname{E}[X\mid\mathfrak{G}] }[/math] to obtain

[math]\displaystyle{ \varphi(\operatorname{E}[X\mid\mathfrak{G}]) \leq \varphi(X)-(D\varphi)(\operatorname{E}[X\mid\mathfrak{G}])\cdot (X-\operatorname{E}[X\mid\mathfrak{G}]). }[/math]

Now, if we take the expectation conditioned to [math]\displaystyle{ \mathfrak{G} }[/math] on both sides of the previous expression, we get the result since:

[math]\displaystyle{ \operatorname{E} \left [\left[(D\varphi)(\operatorname{E}[X\mid\mathfrak{G}])\cdot (X-\operatorname{E}[X\mid\mathfrak{G}])\right]\mid\mathfrak{G} \right] = (D\varphi)(\operatorname{E}[X\mid\mathfrak{G}])\cdot \operatorname{E}[\left( X-\operatorname{E}[X\mid\mathfrak{G}] \right) \mid \mathfrak{G}]=0, }[/math]

by the linearity of the subdifferential in the y variable, and the following well-known property of the conditional expectation:

[math]\displaystyle{ \operatorname{E} \left [ \left(\operatorname{E}[X\mid\mathfrak{G}] \right) \mid\mathfrak{G} \right ] = \operatorname{E}[ X \mid\mathfrak{G}]. }[/math]

Applications and special cases

Form involving a probability density function

Suppose Ω is a measurable subset of the real line and f(x) is a non-negative function such that

[math]\displaystyle{ \int_{-\infty}^\infty f(x)\,dx = 1. }[/math]

In probabilistic language, f is a probability density function.

Then Jensen's inequality becomes the following statement about convex integrals:

If g is any real-valued measurable function and [math]\displaystyle{ \varphi }[/math] is convex over the range of g, then

[math]\displaystyle{ \varphi\left(\int_{-\infty}^\infty g(x)f(x)\, dx\right) \le \int_{-\infty}^\infty \varphi(g(x)) f(x)\, dx. }[/math]

If g(x) = x, then this form of the inequality reduces to a commonly used special case:

[math]\displaystyle{ \varphi\left(\int_{-\infty}^\infty x\, f(x)\, dx\right) \le \int_{-\infty}^\infty \varphi(x)\,f(x)\, dx. }[/math]

This is applied in Variational Bayesian methods.

Example: even moments of a random variable

If g(x) = x²ⁿ, and X is a random variable, then g is convex as

[math]\displaystyle{ \frac{d^{2}g}{dx^{2}}(x) = 2n(2n - 1)x^{2n - 2} \geq 0\quad \forall\ x \in \R }[/math]

and so

[math]\displaystyle{ g(\operatorname{E}[X]) = (\operatorname{E}[X])^{2n} \leq\operatorname{E}[X^{2n}]. }[/math]

In particular, if some even moment 2n of X is finite, X has a finite mean. An extension of this argument shows X has finite moments of every order [math]\displaystyle{ l\in\N }[/math] dividing n.

Alternative finite form

Let Ω = {x₁, ... x_n}, and take μ to be the counting measure on Ω, then the general form reduces to a statement about sums:

[math]\displaystyle{ \varphi\left(\sum_{i=1}^{n} g(x_i)\lambda_i \right) \le \sum_{i=1}^{n} \varphi(g(x_i)) \lambda_i, }[/math]

provided that λ_i ≥ 0 and

[math]\displaystyle{ \lambda_1 + \cdots + \lambda_n = 1. }[/math]

There is also an infinite discrete form.

Statistical physics

Jensen's inequality is of particular importance in statistical physics when the convex function is an exponential, giving:

[math]\displaystyle{ e^{\operatorname{E}[X]} \leq \operatorname{E} \left [ e^X \right ], }[/math]

where the expected values are with respect to some probability distribution in the random variable X.

Proof: Let [math]\displaystyle{ \varphi(x) = e^x }[/math] in [math]\displaystyle{ \varphi\left(\operatorname{E}[X]\right) \leq \operatorname{E} \left[ \varphi(X) \right]. }[/math]

Information theory

If p(x) is the true probability density for X, and q(x) is another density, then applying Jensen's inequality for the random variable Y(X) = q(X)/p(X) and the convex function φ(y) = −log(y) gives

[math]\displaystyle{ \operatorname{E}[\varphi(Y)] \ge \varphi(\operatorname{E}[Y]) }[/math]

Therefore:

[math]\displaystyle{ -D(p(x)\|q(x))=\int p(x) \log \left (\frac{q(x)}{p(x)} \right ) \, dx \le \log \left ( \int p(x) \frac{q(x)}{p(x)}\,dx \right ) = \log \left (\int q(x)\,dx \right ) =0 }[/math]

a result called Gibbs' inequality.

It shows that the average message length is minimised when codes are assigned on the basis of the true probabilities p rather than any other distribution q. The quantity that is non-negative is called the Kullback–Leibler divergence of q from p.

Since −log(x) is a strictly convex function for x > 0, it follows that equality holds when p(x) equals q(x) almost everywhere.

Rao–Blackwell theorem

If L is a convex function and [math]\displaystyle{ \mathfrak{G} }[/math] a sub-sigma-algebra, then, from the conditional version of Jensen's inequality, we get

[math]\displaystyle{ L(\operatorname{E}[\delta(X) \mid \mathfrak{G}]) \le \operatorname{E}[L(\delta(X)) \mid \mathfrak{G}] \quad \Longrightarrow \quad \operatorname{E}[L(\operatorname{E}[\delta(X) \mid \mathfrak{G}])] \le \operatorname{E}[L(\delta(X))]. }[/math]

So if δ(X) is some estimator of an unobserved parameter θ given a vector of observables X; and if T(X) is a sufficient statistic for θ; then an improved estimator, in the sense of having a smaller expected loss L, can be obtained by calculating

[math]\displaystyle{ \delta_1 (X) = \operatorname{E}_{\theta}[\delta(X') \mid T(X')= T(X)], }[/math]

the expected value of δ with respect to θ, taken over all possible vectors of observations X compatible with the same value of T(X) as that observed. Further, because T is a sufficient statistics, [math]\displaystyle{ \delta_1 (X) }[/math] does not depend on θ, hence, becomes a statistics.

This result is known as the Rao–Blackwell theorem.

See also

• Karamata's inequality for a more general inequality
• Popoviciu's inequality
• Law of averages
• A proof without words of Jensen's inequality

References

• David Chandler (1987). Introduction to Modern Statistical Mechanics. Oxford. ISBN 0-19-504277-8. https://archive.org/details/introductiontomo0000chan. 
• Tristan Needham (1993) "A Visual Explanation of Jensen's Inequality", American Mathematical Monthly 100(8):768–71.
• Nicola Fusco; Paolo Marcellini; Carlo Sbordone (1996). Analisi Matematica Due. Liguori. ISBN 978-88-207-2675-1. 
• Walter Rudin (1987). Real and Complex Analysis. McGraw-Hill. ISBN 0-07-054234-1. 
• Rick Durrett (2019). Probability: Theory and Examples (5th ed.). Cambridge University Press. pp. 430. ISBN 978-1108473682. https://services.math.duke.edu/~rtd/PTE/pte.html. Retrieved 21 Dec 2020. 
• Sam Savage (2012) The Flaw of Averages: Why We Underestimate Risk in the Face of Uncertainty (1st ed.) Wiley. ISBN 978-0471381976

External links

• Jensen's Operator Inequality of Hansen and Pedersen.
• Hazewinkel, Michiel, ed. (2001), "Jensen inequality", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/j054220 
• Weisstein, Eric W.. "Jensen's inequality". http://mathworld.wolfram.com/JensensInequality.html. 
• Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format. http://www.mediafire.com/file/1mw1tkgozzu.