Generalized mean
In mathematics, generalized means (or power mean or Hölder mean from Otto Hölder)[1] are a family of functions for aggregating sets of numbers. These include as special cases the Pythagorean means (arithmetic, geometric, and harmonic means).
Definition
If p is a non-zero real number, and [math]\displaystyle{ x_1, \dots, x_n }[/math] are positive real numbers, then the generalized mean or power mean with exponent p of these positive real numbers is[2][3]
[math]\displaystyle{ M_p(x_1,\dots,x_n) = \left( \frac{1}{n} \sum_{i=1}^n x_i^p \right)^{{1}/{p}} . }[/math]
(See p-norm). For p = 0 we set it equal to the geometric mean (which is the limit of means with exponents approaching zero, as proved below):
[math]\displaystyle{ M_0(x_1, \dots, x_n) = \left(\prod_{i=1}^n x_i\right)^{1/n} . }[/math]
Furthermore, for a sequence of positive weights wi we define the weighted power mean as[2] [math]\displaystyle{ M_p(x_1,\dots,x_n) = \left(\frac{\sum_{i=1}^n w_i x_i^p}{\sum_{i=1}^n w_i} \right)^{{1}/{p}} }[/math] and when p = 0, it is equal to the weighted geometric mean:
[math]\displaystyle{ M_0(x_1,\dots,x_n) = \left(\prod_{i=1}^n x_i^{w_i}\right)^{1 / \sum_{i=1}^n w_i} . }[/math]
The unweighted means correspond to setting all wi = 1/n.
Special cases
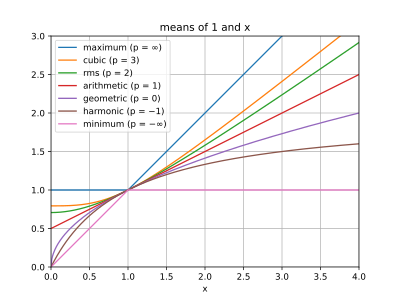
A few particular values of p yield special cases with their own names:[4]
- minimum
- [math]\displaystyle{ M_{-\infty}(x_1,\dots,x_n) = \lim_{p\to-\infty} M_p(x_1,\dots,x_n) = \min \{x_1,\dots,x_n\} }[/math]
- harmonic mean
- [math]\displaystyle{ M_{-1}(x_1,\dots,x_n) = \frac{n}{\frac{1}{x_1}+\dots+\frac{1}{x_n}} }[/math]
- geometric mean [math]\displaystyle{ M_0(x_1,\dots,x_n) = \lim_{p\to0} M_p(x_1,\dots,x_n) = \sqrt[n]{x_1\cdot\dots\cdot x_n} }[/math]
- arithmetic mean
- [math]\displaystyle{ M_1(x_1,\dots,x_n) = \frac{x_1 + \dots + x_n}{n} }[/math]
- root mean square
or quadratic mean[5][6] - [math]\displaystyle{ M_2(x_1,\dots,x_n) = \sqrt{\frac{x_1^2 + \dots + x_n^2}{n}} }[/math]
- cubic mean
- [math]\displaystyle{ M_3(x_1,\dots,x_n) = \sqrt[3]{\frac{x_1^3 + \dots + x_n^3}{n}} }[/math]
- maximum
- [math]\displaystyle{ M_{+\infty}(x_1,\dots,x_n) = \lim_{p\to\infty} M_p(x_1,\dots,x_n) = \max \{x_1,\dots,x_n\} }[/math]
For the purpose of the proof, we will assume without loss of generality that [math]\displaystyle{ w_i \in [0,1] }[/math] and [math]\displaystyle{ \sum_{i=1}^n w_i = 1. }[/math]
We can rewrite the definition of [math]\displaystyle{ M_p }[/math] using the exponential function as
[math]\displaystyle{ M_p(x_1,\dots,x_n) = \exp{\left( \ln{\left[\left(\sum_{i=1}^n w_ix_{i}^p \right)^{1/p}\right]} \right) } = \exp{\left( \frac{\ln{\left(\sum_{i=1}^n w_ix_{i}^p \right)}}{p} \right) } }[/math]
In the limit p → 0, we can apply L'Hôpital's rule to the argument of the exponential function. We assume that p ∈ ℝ but p ≠ 0, and that the sum of wi is equal to 1 (without loss in generality);[7] Differentiating the numerator and denominator with respect to p, we have [math]\displaystyle{ \begin{align} \lim_{p \to 0} \frac{\ln{\left(\sum_{i=1}^n w_ix_{i}^p \right)}}{p} &= \lim_{p \to 0} \frac{\frac{\sum_{i=1}^n w_i x_i^p \ln{x_i}}{\sum_{j=1}^n w_j x_j^p}}{1} \\ &= \lim_{p \to 0} \frac{\sum_{i=1}^n w_i x_i^p \ln{x_i}}{\sum_{j=1}^n w_j x_j^p} \\ &= \frac{\sum_{i=1}^n w_i \ln{x_i}}{\sum_{j=1}^n w_j} \\ &= \sum_{i=1}^n w_i \ln{x_i} \\ &= \ln{\left(\prod_{i=1}^n x_i^{w_i} \right)} \end{align} }[/math]
By the continuity of the exponential function, we can substitute back into the above relation to obtain [math]\displaystyle{ \lim_{p \to 0} M_p(x_1,\dots,x_n) = \exp{\left( \ln{\left(\prod_{i=1}^n x_i^{w_i} \right)} \right)} = \prod_{i=1}^n x_i^{w_i} = M_0(x_1,\dots,x_n) }[/math] as desired.[2]
Assume (possibly after relabeling and combining terms together) that [math]\displaystyle{ x_1 \geq \dots \geq x_n }[/math]. Then
[math]\displaystyle{ \begin{align} \lim_{p \to \infty} M_p(x_1,\dots,x_n) &= \lim_{p \to \infty} \left( \sum_{i=1}^n w_i x_i^p \right)^{1/p} \\ &= x_1 \lim_{p \to \infty} \left( \sum_{i=1}^n w_i \left( \frac{x_i}{x_1} \right)^p \right)^{1/p} \\ &= x_1 = M_\infty (x_1,\dots,x_n). \end{align} }[/math]
The formula for [math]\displaystyle{ M_{-\infty} }[/math] follows from [math]\displaystyle{ M_{-\infty} (x_1,\dots,x_n) = \frac{1}{M_\infty (1/x_1,\dots,1/x_n)} = x_n. }[/math]
Properties
Let [math]\displaystyle{ x_1, \dots, x_n }[/math] be a sequence of positive real numbers, then the following properties hold:[1]
- [math]\displaystyle{ \min(x_1, \dots, x_n) \le M_p(x_1, \dots, x_n) \le \max(x_1, \dots, x_n) }[/math].
- [math]\displaystyle{ M_p(x_1, \dots, x_n) = M_p(P(x_1, \dots, x_n)) }[/math], where [math]\displaystyle{ P }[/math] is a permutation operator.
- [math]\displaystyle{ M_p(b x_1, \dots, b x_n) = b \cdot M_p(x_1, \dots, x_n) }[/math].
- [math]\displaystyle{ M_p(x_1, \dots, x_{n \cdot k}) = M_p\left[M_p(x_1, \dots, x_{k}), M_p(x_{k + 1}, \dots, x_{2 \cdot k}), \dots, M_p(x_{(n - 1) \cdot k + 1}, \dots, x_{n \cdot k})\right] }[/math].
Generalized mean inequality
In general, if p < q, then [math]\displaystyle{ M_p(x_1, \dots, x_n) \le M_q(x_1, \dots, x_n) }[/math] and the two means are equal if and only if x1 = x2 = ... = xn.
The inequality is true for real values of p and q, as well as positive and negative infinity values.
It follows from the fact that, for all real p, [math]\displaystyle{ \frac{\partial}{\partial p}M_p(x_1, \dots, x_n) \geq 0 }[/math] which can be proved using Jensen's inequality.
In particular, for p in {−1, 0, 1}, the generalized mean inequality implies the Pythagorean means inequality as well as the inequality of arithmetic and geometric means.
Proof of the weighted inequality
We will prove the weighted power mean inequality. For the purpose of the proof we will assume the following without loss of generality: [math]\displaystyle{ \begin{align} w_i \in [0, 1] \\ \sum_{i=1}^nw_i = 1 \end{align} }[/math]
The proof for unweighted power means can be easily obtained by substituting wi = 1/n.
Equivalence of inequalities between means of opposite signs
Suppose an average between power means with exponents p and q holds: [math]\displaystyle{ \left(\sum_{i=1}^n w_i x_i^p\right)^{1/p} \geq \left(\sum_{i=1}^n w_i x_i^q\right)^{1/q} }[/math] applying this, then: [math]\displaystyle{ \left(\sum_{i=1}^n\frac{w_i}{x_i^p}\right)^{1/p} \geq \left(\sum_{i=1}^n\frac{w_i}{x_i^q}\right)^{1/q} }[/math]
We raise both sides to the power of −1 (strictly decreasing function in positive reals): [math]\displaystyle{ \left(\sum_{i=1}^nw_ix_i^{-p}\right)^{-1/p} = \left(\frac{1}{\sum_{i=1}^nw_i\frac{1}{x_i^p}}\right)^{1/p} \leq \left(\frac{1}{\sum_{i=1}^nw_i\frac{1}{x_i^q}}\right)^{1/q} = \left(\sum_{i=1}^nw_ix_i^{-q}\right)^{-1/q} }[/math]
We get the inequality for means with exponents −p and −q, and we can use the same reasoning backwards, thus proving the inequalities to be equivalent, which will be used in some of the later proofs.
Geometric mean
For any q > 0 and non-negative weights summing to 1, the following inequality holds: [math]\displaystyle{ \left(\sum_{i=1}^n w_i x_i^{-q}\right)^{-1/q} \leq \prod_{i=1}^n x_i^{w_i} \leq \left(\sum_{i=1}^n w_i x_i^q\right)^{1/q}. }[/math]
The proof follows from Jensen's inequality, making use of the fact the logarithm is concave: [math]\displaystyle{ \log \prod_{i=1}^n x_i^{w_i} = \sum_{i=1}^n w_i\log x_i \leq \log \sum_{i=1}^n w_i x_i. }[/math]
By applying the exponential function to both sides and observing that as a strictly increasing function it preserves the sign of the inequality, we get [math]\displaystyle{ \prod_{i=1}^n x_i^{w_i} \leq \sum_{i=1}^n w_i x_i. }[/math]
Taking q-th powers of the xi yields [math]\displaystyle{ \begin{align} &\prod_{i=1}^n x_i^{q{\cdot}w_i} \leq \sum_{i=1}^n w_i x_i^q \\ &\prod_{i=1}^n x_i^{w_i} \leq \left(\sum_{i=1}^n w_i x_i^q\right)^{1/q}.\end{align} }[/math]
Thus, we are done for the inequality with positive q; the case for negatives is identical but for the swapped signs in the last step:
[math]\displaystyle{ \prod_{i=1}^n x_i^{-q{\cdot}w_i} \leq \sum_{i=1}^n w_i x_i^{-q}. }[/math]
Of course, taking each side to the power of a negative number -1/q swaps the direction of the inequality.
[math]\displaystyle{ \prod_{i=1}^n x_i^{w_i} \geq \left(\sum_{i=1}^n w_i x_i^q\right)^{1/q}. }[/math]
Inequality between any two power means
We are to prove that for any p < q the following inequality holds: [math]\displaystyle{ \left(\sum_{i=1}^n w_i x_i^p\right)^{1/p} \leq \left(\sum_{i=1}^nw_ix_i^q\right)^{1/q} }[/math] if p is negative, and q is positive, the inequality is equivalent to the one proved above: [math]\displaystyle{ \left(\sum_{i=1}^nw_i x_i^p\right)^{1/p} \leq \prod_{i=1}^n x_i^{w_i} \leq \left(\sum_{i=1}^n w_i x_i^q\right)^{1/q} }[/math]
The proof for positive p and q is as follows: Define the following function: f : R+ → R+ [math]\displaystyle{ f(x)=x^{\frac{q}{p}} }[/math]. f is a power function, so it does have a second derivative: [math]\displaystyle{ f''(x) = \left(\frac{q}{p} \right) \left( \frac{q}{p}-1 \right)x^{\frac{q}{p}-2} }[/math] which is strictly positive within the domain of f, since q > p, so we know f is convex.
Using this, and the Jensen's inequality we get: [math]\displaystyle{ \begin{align} f \left( \sum_{i=1}^nw_ix_i^p \right) &\leq \sum_{i=1}^nw_if(x_i^p) \\[3pt] \left(\sum_{i=1}^n w_i x_i^p\right)^{q/p} &\leq \sum_{i=1}^nw_ix_i^q \end{align} }[/math] after raising both side to the power of 1/q (an increasing function, since 1/q is positive) we get the inequality which was to be proven:
[math]\displaystyle{ \left(\sum_{i=1}^n w_i x_i^p\right)^{1/p} \leq \left(\sum_{i=1}^n w_i x_i^q\right)^{1/q} }[/math]
Using the previously shown equivalence we can prove the inequality for negative p and q by replacing them with −q and −p, respectively.
Generalized f-mean
The power mean could be generalized further to the generalized f-mean:
[math]\displaystyle{ M_f(x_1,\dots,x_n) = f^{-1} \left({\frac{1}{n}\cdot\sum_{i=1}^n{f(x_i)}}\right) }[/math]
This covers the geometric mean without using a limit with f(x) = log(x). The power mean is obtained for f(x) = xp. Properties of these means are studied in de Carvalho (2016).[3]
Applications
Signal processing
A power mean serves a non-linear moving average which is shifted towards small signal values for small p and emphasizes big signal values for big p. Given an efficient implementation of a moving arithmetic mean called smooth one can implement a moving power mean according to the following Haskell code.
powerSmooth :: Floating a => ([a] -> [a]) -> a -> [a] -> [a] powerSmooth smooth p = map (** recip p) . smooth . map (**p)
- For big p it can serve as an envelope detector on a rectified signal.
- For small p it can serve as a baseline detector on a mass spectrum.
See also
- Arithmetic–geometric mean
- Average
- Heronian mean
- Inequality of arithmetic and geometric means
- Lehmer mean – also a mean related to powers
- Minkowski distance
- Quasi-arithmetic mean – another name for the generalized f-mean mentioned above
- Root mean square
Notes
References
- ↑ Jump up to: 1.0 1.1 Sýkora, Stanislav (2009). "Mathematical means and averages: basic properties". Stan's Library (Stan’s Library: Castano Primo, Italy) 3 (Volume III). doi:10.3247/SL3Math09.001.
- ↑ Jump up to: 2.0 2.1 2.2 P. S. Bullen: Handbook of Means and Their Inequalities. Dordrecht, Netherlands: Kluwer, 2003, pp. 175-177
- ↑ Jump up to: 3.0 3.1 de Carvalho, Miguel (2016). "Mean, what do you Mean?". The American Statistician 70 (3): 764‒776. doi:10.1080/00031305.2016.1148632. https://zenodo.org/record/895400.
- ↑ Weisstein, Eric W.. "Power Mean". http://mathworld.wolfram.com/PowerMean.html. (retrieved 2019-08-17)
- ↑ Thompson, Sylvanus P. (1965). Calculus Made Easy. Macmillan International Higher Education. p. 185. ISBN 9781349004874. https://books.google.com/books?id=6VJdDwAAQBAJ&pg=PA185. Retrieved 5 July 2020.
- ↑ Jones, Alan R. (2018). Probability, Statistics and Other Frightening Stuff. Routledge. p. 48. ISBN 9781351661386. https://books.google.com/books?id=OvtsDwAAQBAJ&pg=PA48. Retrieved 5 July 2020.
- ↑ Handbook of Means and Their Inequalities (Mathematics and Its Applications).
Further reading
- Bullen, P. S. (2003). "Chapter III - The Power Means". Handbook of Means and Their Inequalities. Dordrecht, Netherlands: Kluwer. pp. 175–265.
External links
 |