Jessen's icosahedron

From HandWiki
Short description: Right-angled non-convex polyhedron
Jessen's icosahedron
Jessen's icosahedron.svg
Faces
Edges
  • 24 short and convex
  • 6 long and concave
Vertices12
Dihedral angle (degrees)90
Properties
Net
Jessen icosahedron net.svg

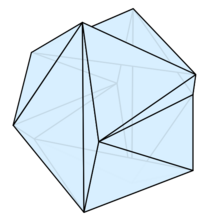
Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same numbers of vertices, edges, and faces as the regular icosahedron. It is named for Børge Jessen, who studied it in 1967.[1] In 1971, a family of nonconvex polyhedra including this shape was independently discovered and studied by Adrien Douady under the name six-beaked shaddock;[2][3] later authors have applied variants of this name more specifically to Jessen's icosahedron.[4]

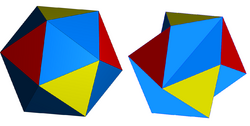
The faces of Jessen's icosahedron meet only in right angles, even though it has no orientation where they are all parallel to the coordinate planes. It is a "shaky polyhedron", meaning that (like a flexible polyhedron) it is not infinitesimally rigid. Outlining the edges of this polyhedron with struts and cables produces a widely-used tensegrity structure,[5] also called the six-bar tensegrity,[6] tensegrity icosahedron, or expanded octahedron.[7]

Construction and geometric properties

File:Jessen icosahedron.stl

View with translucent faces
Distances between selected points

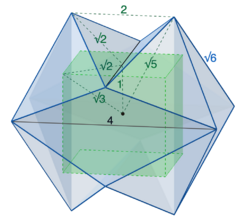
The vertices of Jessen's icosahedron may be chosen to have as their coordinates the twelve triplets given by the cyclic permutations of the coordinates [math]\displaystyle{ (\pm 2, \pm 1, 0) }[/math].[1] With this coordinate representation, the short edges of the icosahedron (the ones with convex angles) have length [math]\displaystyle{ \sqrt{6} }[/math], and the long (reflex) edges have length [math]\displaystyle{ 4 }[/math]. The faces of the icosahedron are eight congruent equilateral triangles with the short side length, and twelve congruent obtuse isosceles triangles with one long edge and two short edges.[8]

Jessen's icosahedron is vertex-transitive (or isogonal), meaning that it has symmetries taking any vertex to any other vertex.[9] Its dihedral angles are all right angles. One can use it as the basis for the construction of an infinite family of combinatorially distinct polyhedra with right dihedral angles, formed by gluing copies of Jessen's icosahedron together on their equilateral-triangle faces.[1]

As with the simpler Schönhardt polyhedron, the interior of Jessen's icosahedron cannot be triangulated into tetrahedra without adding new vertices.[10] However, because its dihedral angles are rational multiples of [math]\displaystyle{ \pi }[/math], it has Dehn invariant equal to zero. Therefore, it is scissors-congruent to a cube, meaning that it can be sliced into smaller polyhedral pieces that can be rearranged to form a solid cube.[1]

It is star-shaped, meaning that there is a point in its interior (for instance its center of symmetry) from which all other points are visible. It provides a counterexample to a question of Michel Demazure asking whether star-shaped polyhedra with triangular faces can be made convex by sliding their vertices along rays from this central point. Demazure had connected this question to a point in algebraic geometry by proving that, for star-shaped polyhedra with triangular faces, a certain algebraic variety associated with the polyhedron would be a projective variety if the polyhedron could be made convex in this way. However, Adrien Douady proved that, for a family of shapes that includes Jessen's icosahedron, this sliding motion cannot result in a convex polyhedron.[2][3] Demazure used this result to construct a non-projective smooth rational complete three-dimensional variety.[11]

Structural rigidity

Het Ding (nl), a tensegrity sculpture whose struts and cables form the outline of Jessen's icosahedron, at the University of Twente
Het Ding (nl), a tensegrity sculpture whose struts and cables form the outline of Jessen's icosahedron, at the University of Twente

Jessen's icosahedron is not a flexible polyhedron: if it is constructed with rigid panels for its faces, connected by hinges, it cannot change shape. However, it is also not infinitesimally rigid. This means that there exists a continuous motion of its vertices that, while not actually preserving the edge lengths and face shapes of the polyhedron, does so to a first-order approximation. As a rigid but not infinitesimally rigid polyhedron, it forms an example of a "shaky polyhedron".[5] Because very small changes in its edge lengths can cause much bigger changes in its angles, physical models of the polyhedron seem to be flexible.[4]

Replacing the long concave-dihedral edges of Jessen's icosahedron by rigid struts, and the shorter convex-dihedral edges by cables or wires, produces the tensegrity icosahedron, the structure which has also been called the "six-bar tensegrity"[6] and the "expanded octahedron".[7] As well as in tensegrity sculptures, this structure is "the most ubiquitous form of tensegrity robots", and the "Skwish" children's toy based on this structure was "pervasive in the 1980's".[6] The "super ball bot" concept based on this design has been proposed by the NASA Institute for Advanced Concepts as a way to enclose space exploration devices for safe landings on other planets.[12][13] Anthony Pugh calls this structure "perhaps the best known, and certainly one of the most impressive tensegrity figures".[7]

Jessen's icosahedron is weakly convex, meaning that its vertices are in convex position, and its existence demonstrates that weakly convex polyhedra need not be infinitesimally rigid. However, it has been conjectured that weakly convex polyhedra that can be triangulated must be infinitesimally rigid, and this conjecture has been proven under the additional assumption that the exterior part of the convex hull of the polyhedron can also be triangulated.[14]

Related shapes

Regular icosahedron and its non-convex variant, which differs from Jessen's icosahedron in having different vertex positions and non-right-angled dihedrals

A similar shape can be formed by keeping the vertices of a regular icosahedron in their original positions and replacing certain pairs of equilateral triangles by pairs of isosceles triangles. This shape has also sometimes incorrectly been called Jessen's icosahedron.[15] However, although the resulting polyhedron has the same combinatorial structure and symmetry as Jessen's icosahedron, and looks similar, it does not form a tensegrity structure,[7] and does not have right-angled dihedrals.

Jessen's icosahedron is one of a continuous family of icosahedra with 20 faces, 8 of which are equilateral triangles and 12 of which are isosceles triangles. Each shape in this family is obtained from a regular octahedron by dividing each of its edges in the same proportion and connecting the division points in the pattern of a regular icosahedron. These shapes can be parameterized by the proportion into which the octahedron edges are divided. The convex shapes in this family range from the octahedron itself through the regular icosahedron to the cuboctahedron, with its square faces subdivided into two right triangles in a flat plane. Extending the range of the parameter past the proportion that gives the cuboctahedron produces non-convex shapes, including Jessen's icosahedron. This family was described by H. S. M. Coxeter in 1947.[16] Later, the twisting, expansive-contractive transformations between members of this family, parameterized differently in order to maintain a constant value for one of the two edge lengths, were named jitterbug transformations by Buckminster Fuller.[17]

In 2018, Jessen's icosahedron was generalized by V. A. Gor’kavyi and A. D. Milka (uk) to an infinite family of rigid but not infinitesimally rigid polyhedra. These polyhedra are combinatorially distinct, and have chiral dihedral symmetry groups of arbitrarily large order. However, unlike Jessen's icosahedron, not all of their faces are triangles.[18]

References

  1. ↑ 1.0 1.1 1.2 1.3 "Orthogonal icosahedra". Nordisk Matematisk Tidskrift 15 (2): 90–96. 1967. 
  2. ↑ 2.0 2.1 Geometry. Universitext. II. Springer-Verlag. 1987. pp. 47. 
  3. ↑ 3.0 3.1 "Le shaddock à six becs" (in French). Bulletin A.P.M.E.P. 281: 699–701. 1971. https://www.apmep.fr/IMG/pdf/AAA71038.pdf. 
  4. ↑ 4.0 4.1 Gorkavyy, V.; Kalinin, D. (2016). "On model flexibility of the Jessen orthogonal icosahedron". Beiträge zur Algebra und Geometrie 57 (3): 607–622. doi:10.1007/s13366-016-0287-5. 
  5. ↑ 5.0 5.1 Goldberg, Michael (1978). "Unstable polyhedral structures". Mathematics Magazine 51 (3): 165–170. doi:10.2307/2689996. 
  6. ↑ 6.0 6.1 6.2 Cera, Angelo Brian Micubo (2020). Design, Control, and Motion Planning of Cable-Driven Flexible Tensegrity Robots (Ph.D. thesis). University of California, Berkeley. p. 5.
  7. ↑ 7.0 7.1 7.2 7.3 Pugh, Anthony (1976). An Introduction to Tensegrity. University of California Press. pp. 11, 26. ISBN 9780520030558. https://books.google.com/books?id=McEOfJu3NQAC&pg=PA11. 
  8. ↑ Kim, Kyunam; Agogino, Adrian K. (June 2020). "Rolling locomotion of cable-driven soft spherical tensegrity robots". Soft Robotics 7 (3): 346–361. doi:10.1089/soro.2019.0056. PMID 32031916. 
  9. ↑ Grünbaum, Branko (1999). "Acoptic polyhedra". Advances in Discrete and Computational Geometry (South Hadley, MA, 1996). Contemporary Mathematics. 223. Providence, Rhode Island: American Mathematical Society. pp. 163–199. doi:10.1090/conm/223/03137. https://sites.math.washington.edu/~grunbaum/BG225.Acoptic%20polyhedra.pdf. Retrieved 2019-10-16. 
  10. ↑ Bezdek, Andras; Carrigan, Braxton (2016). "On nontriangulable polyhedra". Beiträge zur Algebra und Geometrie 57 (1): 51–66. doi:10.1007/s13366-015-0248-4. 
  11. ↑ "Sous-groupes algébriques de rang maximum du groupe de Cremona" (in French). Annales Scientifiques de l'École Normale Supérieure 3 (4): 507–588. 1970. doi:10.24033/asens.1201. https://www.numdam.org/item?id=ASENS_1970_4_3_4_507_0.  See appendix.
  12. ↑ Stinson, Liz (February 26, 2014). "NASA's Latest Robot: A Rolling Tangle of Rods That Can Take a Beating". Wired. https://www.wired.com/2014/02/nasas-super-ball-bot-revolutionize-robotics/. 
  13. ↑ Agogino, Adrian; SunSpiral, Vytas; Atkinson, David (June 2013). "Final Report: Super Ball Bot - Structures for Planetary Landing and Exploration for the NASA Innovative Advanced Concepts (NIAC) Program". NASA Ames Research Center. https://ti.arc.nasa.gov/publications/10049/download/. 
  14. ↑ Izmestiev, Ivan; Schlenker, Jean-Marc (2010). "Infinitesimal rigidity of polyhedra with vertices in convex position". Pacific Journal of Mathematics 248 (1): 171–190. doi:10.2140/pjm.2010.248.171. 
  15. ↑ Incorrect descriptions of Jessen's icosahedron as having the same vertex positions as a regular icosahedron include:
  16. ↑ "Section 3.7: Coordinates for the vertices of the regular and quasi-regular solids". Regular Polytopes (3rd ed.). New York: Dover. 1973. ; 1st ed., Methuen, 1947
  17. ↑ Verheyen, H. F. (1989). "The complete set of Jitterbug transformers and the analysis of their motion". Computers and Mathematics with Applications 17 (1–3): 203–250. doi:10.1016/0898-1221(89)90160-0. 
  18. ↑ Gorkavyi, V. A.; Milka, A. D. (2018). "Birosettes are model flexors". Ukrainian Math. J. 70 (7): 1022–1041. doi:10.1007/s11253-018-1549-1. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Jessen%27s_icosahedron&oldid=3365094"