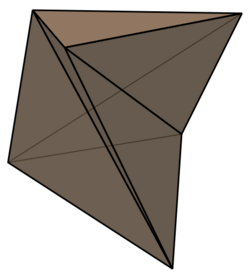
Schönhardt polyhedron
File:Schönhardt polyhedron.stl In geometry, the Schönhardt polyhedron is the simplest non-convex polyhedron that cannot be triangulated into tetrahedra without adding new vertices. It is named after German mathematician Erich Schönhardt, who described it in 1928.[1] The same polyhedra have also been studied in connection with Cauchy's rigidity theorem as an example where polyhedra with two different shapes have faces of the same shapes.
Construction
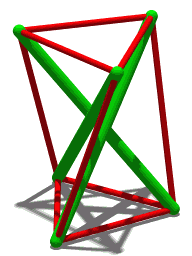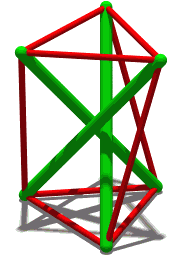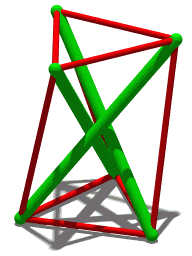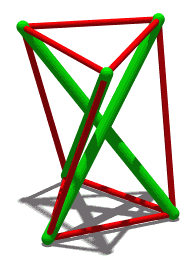
One way of constructing the Schönhardt polyhedron starts with a triangular prism, with two parallel equilateral triangles as its faces. One of the triangles is rotated around the centerline of the prism, breaking the square faces of the prism into pairs of triangles. If each of these pairs is chosen to be non-convex, the Schönhardt polyhedron is the result.[2]
Properties
The Schönhardt polyhedron has six vertices, twelve edges, and eight triangular faces. The six vertices of the Schönhardt polyhedron can be used to form fifteen unordered pairs of vertices. Twelve of these fifteen pairs form edges of the polyhedron: there are six edges in the two equilateral triangle faces, and six edges connecting the two triangles. The remaining three edges form diagonals of the polyhedron, but lie entirely outside the polyhedron.[3]
The convex hull of the Schönhardt polyhedron is another polyhedron with the same six vertices, and a different set of twelve edges and eight triangular faces; like the Schönhardt polyhedron, it is combinatorially equivalent to a regular octahedron. The symmetric difference of the Schönhardt polyhedron consists of three tetrahedra, each lying between one of the concave dihedral edges of the Schönhardt polyhedron and one of the exterior diagonals. Thus, the Schönhardt polyhedron can be formed by removing these three tetrahedra from a convex (but irregular) octahedron.[4]
Impossibility of triangulation
It is impossible to partition the Schönhardt polyhedron into tetrahedra whose vertices are vertices of the polyhedron. More strongly, there is no tetrahedron that lies entirely inside the Schönhardt polyhedron and has vertices of the polyhedron as its four vertices. This follows from the following two properties of the Schönhardt polyhedron:[3]
- Every triangle formed by its edges is one of its faces. Therefore, because it is not a tetrahedron itself, every tetrahedron formed by four of its vertices must have an edge that it does not share with the Schönhardt polyhedron.[3]
- Every diagonal that connects two of its vertices but is not an edge of the Schönhardt polyhedron lies outside the polyhedron. Therefore, every tetrahedron that uses such a diagonal as one of its edges must also lie in part outside the Schönhardt polyhedron.[3]
Jumping polyhedron
In connection with the theory of flexible polyhedra, instances of the Schönhardt polyhedron form a "jumping polyhedron": a polyhedron that has two different rigid states, both having the same face shapes and the same orientation (convex or concave) of each edge. A model whose surface is made of a stiff but somewhat deformable material, such as cardstock, can be made to "jump" between the two shapes. A solid model could not change shape in this way. Neither could a model made of a more rigid material like glass: although it could exist in either of the two shapes, it would be unable to deform sufficiently to move between them. This stands in contrast to Cauchy's rigidity theorem, according to which, for each convex polyhedron, there is no other polyhedron having the same face shapes and edge orientations.[5]
Related constructions
It was shown by (Rambau 2005) that the Schönhardt polyhedron can be generalized to other polyhedra, combinatorially equivalent to antiprisms, that cannot be triangulated. These polyhedra are formed by connecting regular k-gons in two parallel planes, twisted with respect to each other, in such a way that k of the 2k edges that connect the two k-gons have concave dihedrals. For sufficiently small twisting angles, the result has no triangulation.[4][6] Another polyhedron that cannot be triangulated is Jessen's icosahedron, combinatorially equivalent to a regular icosahedron.[2]
In a different direction, (Bagemihl 1948) constructed a polyhedron that shares with the Schönhardt polyhedron the property that it has no internal diagonals. The tetrahedron and the Császár polyhedron have no diagonals at all: every pair of vertices in these polyhedra forms an edge.[3] It remains an open question whether there are any other polyhedra (with manifold boundary) without diagonals,[7] although there exist non-manifold surfaces with no diagonals and any number of vertices greater than five.[8]
Applications
(Ruppert Seidel) used Schönhardt's polyhedron as the basis for a proof that it is NP-complete to determine whether a non-convex polyhedron can be triangulated. The proof uses many copies of the Schönhardt polyhedron, with its top face removed, as gadgets within a larger polyhedron. Any triangulation of the overall polyhedron must include a tetrahedron connecting the bottom face of each gadget to a vertex in the rest of the polyhedron that can see this bottom face. The complex pattern of obstructions between tetrahedra of this type can be used to simulate Boolean logic components in a reduction from the Boolean satisfiability problem.[4][10]
References
- ↑ "Über die Zerlegung von Dreieckspolyedern in Tetraeder", Mathematische Annalen 98: 309–312, 1928, doi:10.1007/BF01451597, http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=27796
- ↑ 2.0 2.1 Bezdek, Andras; Carrigan, Braxton (2016), "On nontriangulable polyhedra", Beiträge zur Algebra und Geometrie 57 (1): 51–66, doi:10.1007/s13366-015-0248-4
- ↑ 3.0 3.1 3.2 3.3 3.4 "On indecomposable polyhedra", American Mathematical Monthly 55 (7): 411–413, 1948, doi:10.2307/2306130
- ↑ 4.0 4.1 4.2 "Example 3.6.1: Schönhardt’s polyhedron", Triangulations: Structures for algorithms and applications, Algorithms and Computation in Mathematics, 25, Berlin: Springer-Verlag, 2010, pp. 133–134, doi:10.1007/978-3-642-12971-1, ISBN 978-3-642-12970-4
- ↑ Grünbaum, Branko (1975), Lectures on lost mathematics, pp. 41–42, https://digital.lib.washington.edu/researchworks/bitstream/handle/1773/15700/Lost%20Mathematics.pdf?fterence=1
- ↑ Rambau, J. (2005), "On a generalization of Schönhardt's polyhedron", Combinatorial and Computational Geometry, MSRI Publications, 52, Cambridge: Cambridge University Press, pp. 501–516, https://www.msri.org/communications/books/Book52/files/27rambau.pdf
- ↑ Ziegler, Günter M. (2008), "Polyhedral surfaces of high genus", in Bobenko, A. I.; Schröder, P.; Sullivan, J. M. et al., Discrete Differential Geometry, Oberwolfach Seminars, 38, Springer-Verlag, pp. 191–213, doi:10.1007/978-3-7643-8621-4_10, math.MG/0412093, ISBN 978-3-7643-8620-7
- ↑ Szabó, Sándor (1984), "Polyhedra without diagonals", Periodica Mathematica Hungarica 15 (1): 41–49, doi:10.1007/BF02109370; Szabó, Sándor (2009), "Polyhedra without diagonals II", Periodica Mathematica Hungarica 58 (2): 181–187, doi:10.1007/s10998-009-10181-x
- ↑ Tobie, Roger (2012). "Proceeding of the Natural Philosophy Alliance, 19th Annual Conference, 25-28 July, 2012, Albquerque, New Mexico". 9. Lulu Press. p. 628. ISBN 978-1-105-95509-9.
- ↑ Ruppert, J. (1992), "On the difficulty of triangulating three-dimensional nonconvex polyhedra", Discrete & Computational Geometry 7: 227–253, doi:10.1007/BF02187840
External links
- Three Untetrahedralizable Objects, D. Eppstein. Includes a rotatable 3d model of the Schönhardt polyhedron.
 |