Kaniadakis exponential distribution
The Kaniadakis exponential distribution (or κ-exponential distribution) is a probability distribution arising from the maximization of the Kaniadakis entropy under appropriate constraints. It is one example of a Kaniadakis distribution. The κ-exponential is a generalization of the exponential distribution in the same way that Kaniadakis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy.[1] The κ-exponential distribution of Type I is a particular case of the κ-Gamma distribution, whilst the κ-exponential distribution of Type II is a particular case of the κ-Weibull distribution.
Type I
Probability density function
|
Probability density function 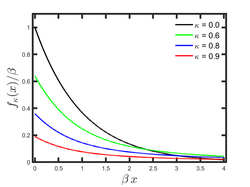 | |||
|
Cumulative distribution function  | |||
| Parameters |
[math]\displaystyle{ 0 \lt \kappa \lt 1 }[/math] shape (real) [math]\displaystyle{ \beta\gt 0 }[/math] rate (real) | ||
|---|---|---|---|
| Support | [math]\displaystyle{ x \in [0, \infty) }[/math] | ||
| [math]\displaystyle{ (1 - \kappa^2) \beta \exp_\kappa(-\beta x) }[/math] | |||
| CDF | [math]\displaystyle{ 1-\Big(\sqrt{1+\kappa^2\beta^2 x^2} + \kappa^2 \beta x \Big)\exp_k({-\beta x)} }[/math] | ||
| Mean | [math]\displaystyle{ \frac{1}{\beta} \frac{1 - \kappa^2}{1 - 4\kappa^2} }[/math] | ||
| Variance | [math]\displaystyle{ \sigma_\kappa^2 =\frac{1}{\beta^2} \frac{2(1-4\kappa^2)^2 - (1 - \kappa^2)^2(1-9\kappa^2)}{(1-4\kappa^2)^2(1-9\kappa^2)} }[/math] | ||
| Skewness | [math]\displaystyle{ \frac{ 2 (1-\kappa^2) (144 \kappa^8+23 \kappa^6+27 \kappa^4-6 \kappa^2+1) }{ \beta^3 \sigma^3_\kappa (4 \kappa^2-1)^3 (144 \kappa^4-25 \kappa^2+1) } }[/math] | ||
| Kurtosis | [math]\displaystyle{ \frac{ 9(1200\kappa^{14} - 6123\kappa^{12} + 562\kappa^{10} +1539 \kappa^8 - 544 \kappa^6 + 143 \kappa^4 -18\kappa^2 + 1 )}{ \beta^4 \sigma_\kappa^4 (1-\kappa^2)^{-1}(1 - 4\kappa^2)^4 (3600\kappa^8 -4369\kappa^6 + 819\kappa^4 - 51\kappa^2 + 1) } - 3 }[/math] | ||
The Kaniadakis κ-exponential distribution of Type I is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics which exhibit power-law tails. This distribution has the following probability density function:[2]
- [math]\displaystyle{ f_{_{\kappa}}(x) = (1 - \kappa^2) \beta \exp_\kappa(-\beta x) }[/math]
valid for [math]\displaystyle{ x \ge 0 }[/math], where [math]\displaystyle{ 0 \leq |\kappa| \lt 1 }[/math] is the entropic index associated with the Kaniadakis entropy and [math]\displaystyle{ \beta \gt 0 }[/math] is known as rate parameter. The exponential distribution is recovered as [math]\displaystyle{ \kappa \rightarrow 0. }[/math]
Cumulative distribution function
The cumulative distribution function of κ-exponential distribution of Type I is given by
- [math]\displaystyle{ F_\kappa(x) = 1-\Big(\sqrt{1+\kappa^2\beta^2 x^2} + \kappa^2 \beta x \Big)\exp_k({-\beta x)} }[/math]
for [math]\displaystyle{ x \ge 0 }[/math]. The cumulative exponential distribution is recovered in the classical limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Properties
Moments, expectation value and variance
The κ-exponential distribution of type I has moment of order [math]\displaystyle{ m \in \mathbb{N} }[/math] given by[2]
- [math]\displaystyle{ \operatorname{E}[X^m] = \frac{1 - \kappa^2}{\prod_{n=0}^{m+1} [1-(2n-m-1) \kappa ]} \frac{m!}{\beta^m} }[/math]
where [math]\displaystyle{ f_\kappa(x) }[/math] is finite if [math]\displaystyle{ 0 \lt m + 1 \lt 1/\kappa }[/math].
The expectation is defined as:
- [math]\displaystyle{ \operatorname{E}[X] = \frac{1}{\beta} \frac{1 - \kappa^2}{1 - 4\kappa^2} }[/math]
and the variance is:
- [math]\displaystyle{ \operatorname{Var}[X] = \sigma_\kappa^2 = \frac{1}{\beta^2} \frac{2(1-4\kappa^2)^2 - (1 - \kappa^2)^2(1-9\kappa^2)}{(1-4\kappa^2)^2(1-9\kappa^2)} }[/math]
Kurtosis
The kurtosis of the κ-exponential distribution of type I may be computed thought:
- [math]\displaystyle{ \operatorname{Kurt}[X] = \operatorname{E}\left[\frac{\left[ X - \frac{1}{\beta} \frac{1 - \kappa^2}{1 - 4\kappa^2}\right]^4}{\sigma_\kappa^4}\right] }[/math]
Thus, the kurtosis of the κ-exponential distribution of type I distribution is given by:
[math]\displaystyle{ \operatorname{Kurt}[X] = \frac{ 9(1-\kappa^2)(1200\kappa^{14} - 6123\kappa^{12} + 562\kappa^{10} +1539 \kappa^8 - 544 \kappa^6 + 143 \kappa^4 -18\kappa^2 + 1 )}{ \beta^4 \sigma_\kappa^4 (1 - 4\kappa^2)^4 (3600\kappa^8 -4369\kappa^6 + 819\kappa^4 - 51\kappa^2 + 1) } \quad \text{for} \quad 0 \leq \kappa \lt 1/5 }[/math]
or
[math]\displaystyle{ \operatorname{Kurt}[X] = \frac{ 9(9\kappa^2-1)^2(\kappa^2-1)(1200\kappa^{14} - 6123\kappa^{12} + 562\kappa^{10} +1539 \kappa^8 - 544 \kappa^6 + 143 \kappa^4 -18\kappa^2 + 1 )}{ \beta^2 (1 - 4\kappa^2)^2(9\kappa^6 + 13\kappa^4 - 5\kappa^2 +1)(3600\kappa^8 -4369\kappa^6 + 819\kappa^4 - 51\kappa^2 + 1) } \quad \text{for} \quad 0 \leq \kappa \lt 1/5 }[/math]
The kurtosis of the ordinary exponential distribution is recovered in the limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Skewness
The skewness of the κ-exponential distribution of type I may be computed thought:
- [math]\displaystyle{ \operatorname{Skew}[X] = \operatorname{E}\left[\frac{\left[ X - \frac{1}{\beta} \frac{1 - \kappa^2}{1 - 4\kappa^2}\right]^3}{\sigma_\kappa^3}\right] }[/math]
Thus, the skewness of the κ-exponential distribution of type I distribution is given by:
[math]\displaystyle{ \operatorname{Shew}[X] = \frac{ 2 (1-\kappa^2) (144 \kappa^8+23 \kappa^6+27 \kappa^4-6 \kappa^2+1) }{ \beta^3 \sigma^3_\kappa (4 \kappa^2-1)^3 (144 \kappa^4-25 \kappa^2+1) } \quad \text{for} \quad 0 \leq \kappa \lt 1/4 }[/math]
The kurtosis of the ordinary exponential distribution is recovered in the limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Type II
Probability density function
|
Probability density function  | |||
|
Cumulative distribution function 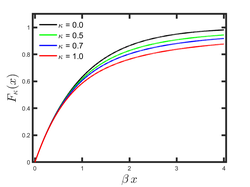 | |||
| Parameters |
[math]\displaystyle{ 0 \leq \kappa \lt 1 }[/math] shape (real) [math]\displaystyle{ \beta\gt 0 }[/math] rate (real) | ||
|---|---|---|---|
| Support | [math]\displaystyle{ x \in [0, \infty) }[/math] | ||
| [math]\displaystyle{ \frac{ \beta }{ \sqrt{1+ \kappa^2 \beta^2 x^2 } } \exp_\kappa(- \beta x) }[/math] | |||
| CDF | [math]\displaystyle{ 1-\exp_k({-\beta x)} }[/math] | ||
| Quantile | [math]\displaystyle{ \beta^{-1} \ln_\kappa \Bigg(\frac{1}{1 - F_\kappa} \Bigg) , 0 \leq F_\kappa \leq 1 }[/math] | ||
| Mean | [math]\displaystyle{ \frac{1}{\beta} \frac{1}{1 - \kappa^2} }[/math] | ||
| Median | [math]\displaystyle{ \beta^{-1} \ln_\kappa (2) }[/math] | ||
| Mode | [math]\displaystyle{ \frac{ 1 }{ \kappa \beta \sqrt{ 2 (1 - \kappa^2) } } }[/math] | ||
| Variance | [math]\displaystyle{ \sigma_\kappa^2 = \frac{1}{\beta^2} \frac{1+2 \kappa^4}{(1-4\kappa^2)(1-\kappa^2)^2} }[/math] | ||
| Skewness | [math]\displaystyle{ \frac{ 2 (15 \kappa^6+6 \kappa^4+2 \kappa^2+1) }{ (1 - 9\kappa^2)(2 \kappa^4 + 1) } \sqrt{ \frac{1 - 4\kappa^2 }{ 1 + 2\kappa^4 } } }[/math] | ||
| Kurtosis | [math]\displaystyle{ \frac{3 (72 \kappa^{10} - 360 \kappa^8 - 44 \kappa^6-32 \kappa^4+7 \kappa^2-3) }{ (4\kappa^2-1)^{-1} (2 \kappa^4+1)^2 (144 \kappa^4-25 \kappa^2+1) } }[/math] | ||
The Kaniadakis κ-exponential distribution of Type II also is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics which exhibit power-law tails, but with different constraints. This distribution is a particular case of the Kaniadakis κ-Weibull distribution with [math]\displaystyle{ \alpha = 1 }[/math] is:[2]
- [math]\displaystyle{ f_{_{\kappa}}(x) = \frac{\beta}{\sqrt{1+\kappa^2 \beta^2 x^2}} \exp_\kappa(-\beta x) }[/math]
valid for [math]\displaystyle{ x \ge 0 }[/math], where [math]\displaystyle{ 0 \leq |\kappa| \lt 1 }[/math] is the entropic index associated with the Kaniadakis entropy and [math]\displaystyle{ \beta \gt 0 }[/math] is known as rate parameter.
The exponential distribution is recovered as [math]\displaystyle{ \kappa \rightarrow 0. }[/math]
Cumulative distribution function
The cumulative distribution function of κ-exponential distribution of Type II is given by
- [math]\displaystyle{ F_\kappa(x) = 1-\exp_k({-\beta x)} }[/math]
for [math]\displaystyle{ x \ge 0 }[/math]. The cumulative exponential distribution is recovered in the classical limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Properties
Moments, expectation value and variance
The κ-exponential distribution of type II has moment of order [math]\displaystyle{ m \lt 1/\kappa }[/math] given by[2]
- [math]\displaystyle{ \operatorname{E}[X^m] = \frac{\beta^{-m} m!}{\prod_{n=0}^{m} [1-(2n- m) \kappa ]} }[/math]
The expectation value and the variance are:
- [math]\displaystyle{ \operatorname{E}[X] = \frac{1}{\beta} \frac{1}{1 - \kappa^2} }[/math]
- [math]\displaystyle{ \operatorname{Var}[X] = \sigma_\kappa^2 = \frac{1}{\beta^2} \frac{1+2 \kappa^4}{(1-4\kappa^2)(1-\kappa^2)^2} }[/math]
The mode is given by:
- [math]\displaystyle{ x_{\textrm{mode}} = \frac{1}{\kappa \beta\sqrt{2(1-\kappa^2)}} }[/math]
Kurtosis
The kurtosis of the κ-exponential distribution of type II may be computed thought:
- [math]\displaystyle{ \operatorname{Kurt}[X] = \operatorname{E}\left[\left(\frac{X - \frac{1}{\beta} \frac{1}{1 - \kappa^2} }{\sigma_\kappa} \right)^4 \right] }[/math]
Thus, the kurtosis of the κ-exponential distribution of type II distribution is given by:
- [math]\displaystyle{ \operatorname{Kurt}[X] = \frac{3 (72 \kappa^{10} - 360 \kappa^8 - 44 \kappa^6-32 \kappa^4+7 \kappa^2-3) }{ \beta^4 \sigma_\kappa^4 (\kappa^2 - 1)^4 (576 \kappa^6 - 244 \kappa^4 + 29 \kappa^2 - 1) } \quad \text{ for } \quad 0 \leq \kappa \lt 1/4 }[/math]
or
- [math]\displaystyle{ \operatorname{Kurt}[X] = \frac{3 (72 \kappa^{10} - 360 \kappa^8 - 44 \kappa^6-32 \kappa^4+7 \kappa^2-3) }{ (4\kappa^2-1)^{-1} (2 \kappa^4+1)^2 (144 \kappa^4-25 \kappa^2+1) } \quad \text{ for } \quad 0 \leq \kappa \lt 1/4 }[/math]
Skewness
The skewness of the κ-exponential distribution of type II may be computed thought:
- [math]\displaystyle{ \operatorname{Skew}[X] = \operatorname{E}\left[\frac{\left[ X - \frac{1}{\beta} \frac{1}{1 - \kappa^2}\right]^3}{\sigma_\kappa^3}\right] }[/math]
Thus, the skewness of the κ-exponential distribution of type II distribution is given by:
[math]\displaystyle{ \operatorname{Skew}[X] = -\frac{ 2 (15 \kappa^6+6 \kappa^4+2 \kappa^2+1) }{ \beta^3 \sigma_\kappa^3 (\kappa^2 - 1)^3 (36 \kappa^4 - 13 \kappa^2 + 1) } \quad \text{for} \quad 0 \leq \kappa \lt 1/3 }[/math]
or
[math]\displaystyle{ \operatorname{Skew}[X] = \frac{ 2 (15 \kappa^6+6 \kappa^4+2 \kappa^2+1) }{ (1 - 9\kappa^2)(2 \kappa^4 + 1) } \sqrt{ \frac{1 - 4\kappa^2 }{ 1 + 2\kappa^4 } } \quad \text{for} \quad 0 \leq \kappa \lt 1/3 }[/math]
The skewness of the ordinary exponential distribution is recovered in the limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Quantiles
The quantiles are given by the following expression
[math]\displaystyle{ x_{\textrm{quantile}} (F_\kappa) = \beta^{-1} \ln_\kappa \Bigg(\frac{1}{1 - F_\kappa} \Bigg) }[/math]
with [math]\displaystyle{ 0 \leq F_\kappa \leq 1 }[/math], in which the median is the case :
[math]\displaystyle{ x_{\textrm{median}} (F_\kappa) = \beta^{-1} \ln_\kappa (2) }[/math]
Lorenz curve
The Lorenz curve associated with the κ-exponential distribution of type II is given by:[2]
- [math]\displaystyle{ \mathcal{L}_\kappa(F_\kappa) = 1 + \frac{1 - \kappa}{2 \kappa}(1 - F_\kappa)^{1 + \kappa} - \frac{1 + \kappa}{2 \kappa}(1 - F_\kappa)^{1 - \kappa} }[/math]
The Gini coefficient is
[math]\displaystyle{ \operatorname{G}_\kappa = \frac{2 + \kappa^2}{4 - \kappa^2} }[/math]
Asymptotic behavior
The κ-exponential distribution of type II behaves asymptotically as follows:[2]
- [math]\displaystyle{ \lim_{x \to +\infty} f_\kappa (x) \sim \kappa^{-1} (2 \kappa \beta)^{-1/\kappa} x^{(-1 - \kappa)/\kappa} }[/math]
- [math]\displaystyle{ \lim_{x \to 0^+} f_\kappa (x) = \beta }[/math]
Applications
The κ-exponential distribution has been applied in several areas, such as:
- In geomechanics, for analyzing the properties of rock masses;[3]
- In quantum theory, in physical analysis using Planck's radiation law;[4]
- In inverse problems, the κ-exponential distribution has been used to formulate a robust approach;[5]
- In Network theory.[6]
See also
- Giorgio Kaniadakis
- Kaniadakis statistics
- Kaniadakis distribution
- Kaniadakis κ-Gaussian distribution
- Kaniadakis κ-Gamma distribution
- Kaniadakis κ-Weibull distribution
- Kaniadakis κ-Logistic distribution
- Kaniadakis κ-Erlang distribution
- Exponential distribution
References
- ↑ Kaniadakis, G. (2001). "Non-linear kinetics underlying generalized statistics" (in en). Physica A: Statistical Mechanics and Its Applications 296 (3–4): 405–425. doi:10.1016/S0378-4371(01)00184-4. Bibcode: 2001PhyA..296..405K. https://linkinghub.elsevier.com/retrieve/pii/S0378437101001844.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters 133 (1): 10002. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. Bibcode: 2021EL....13310002K. https://iopscience.iop.org/article/10.1209/0295-5075/133/10002.
- ↑ Oreste, Pierpaolo; Spagnoli, Giovanni (2018-04-03). "Statistical analysis of some main geomechanical formulations evaluated with the Kaniadakis exponential law" (in en). Geomechanics and Geoengineering 13 (2): 139–145. doi:10.1080/17486025.2017.1373201. ISSN 1748-6025. https://www.tandfonline.com/doi/full/10.1080/17486025.2017.1373201.
- ↑ Ourabah, Kamel; Tribeche, Mouloud (2014). "Planck radiation law and Einstein coefficients reexamined in Kaniadakis κ statistics" (in en). Physical Review E 89 (6): 062130. doi:10.1103/PhysRevE.89.062130. ISSN 1539-3755. PMID 25019747. Bibcode: 2014PhRvE..89f2130O. https://link.aps.org/doi/10.1103/PhysRevE.89.062130.
- ↑ da Silva, Sérgio Luiz E. F.; dos Santos Lima, Gustavo Z.; Volpe, Ernani V.; de Araújo, João M.; Corso, Gilberto (2021). "Robust approaches for inverse problems based on Tsallis and Kaniadakis generalised statistics" (in en). The European Physical Journal Plus 136 (5): 518. doi:10.1140/epjp/s13360-021-01521-w. ISSN 2190-5444. Bibcode: 2021EPJP..136..518D. https://link.springer.com/10.1140/epjp/s13360-021-01521-w.
- ↑ Macedo-Filho, A.; Moreira, D.A.; Silva, R.; da Silva, Luciano R. (2013). "Maximum entropy principle for Kaniadakis statistics and networks" (in en). Physics Letters A 377 (12): 842–846. doi:10.1016/j.physleta.2013.01.032. Bibcode: 2013PhLA..377..842M.
External links
 |

