Kaniadakis logistic distribution
|
Probability density function  Plot of the κ-Logistic distribution for typical κ-values and [math]\displaystyle{ \beta = 1 }[/math]. The case [math]\displaystyle{ \kappa = 0 }[/math] corresponds to the ordinary Logistic distribution. | |||
|
Cumulative distribution function 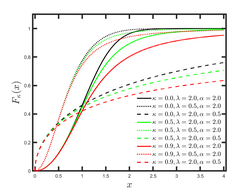 Plots of the cumulative κ-Logistic distribution for typical κ-values and [math]\displaystyle{ \beta = 1 }[/math]. The case [math]\displaystyle{ \kappa = 0 }[/math] corresponds to the ordinary Logistic case. | |||
| Parameters |
[math]\displaystyle{ 0 \leq \kappa \lt 1 }[/math] [math]\displaystyle{ \alpha \gt 0 }[/math] shape (real) [math]\displaystyle{ \beta\gt 0 }[/math] rate (real) [math]\displaystyle{ \lambda \gt 0 }[/math] | ||
|---|---|---|---|
| Support | [math]\displaystyle{ x \in [0, \infty) }[/math] | ||
| [math]\displaystyle{ \frac{\lambda \alpha \beta x^{\alpha-1} }{\sqrt{1+\kappa^2 \beta^2 x^{2\alpha} } } \frac{ \exp_\kappa(-\beta x^\alpha) }{ [ 1 + (\lambda - 1) \exp_\kappa(-\beta x^\alpha)]^2 } }[/math] | |||
| CDF | [math]\displaystyle{ \frac{ 1 - \exp_\kappa(-\beta x^\alpha) }{ 1 + (\lambda - 1) \exp_\kappa(-\beta x^\alpha) } }[/math] | ||
The Kaniadakis Logistic distribution (also known as κ-Logisticdistribution) is a generalized version of the Logistic distribution associated with the Kaniadakis statistics. It is one example of a Kaniadakis distribution. The κ-Logistic probability distribution describes the population kinetics behavior of bosonic ([math]\displaystyle{ 0 \lt \lambda \lt 1 }[/math]) or fermionic ([math]\displaystyle{ \lambda \gt 1 }[/math]) character.[1]
Definitions
Probability density function
The Kaniadakis κ-Logistic distribution is a four-parameter family of continuous statistical distributions, which is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics. This distribution has the following probability density function:[1]
- [math]\displaystyle{ f_{_{\kappa}}(x) = \frac{\lambda \alpha \beta x^{\alpha-1}}{\sqrt{1+\kappa^2 \beta^2 x^{2\alpha} }} \frac{ \exp_\kappa(-\beta x^\alpha) }{ [ 1 + (\lambda - 1) \exp_\kappa(-\beta x^\alpha)]^2 } }[/math]
valid for [math]\displaystyle{ x \geq 0 }[/math], where [math]\displaystyle{ 0 \leq |\kappa| \lt 1 }[/math] is the entropic index associated with the Kaniadakis entropy, [math]\displaystyle{ \beta \gt 0 }[/math] is the rate parameter, [math]\displaystyle{ \lambda \gt 0 }[/math], and [math]\displaystyle{ \alpha \gt 0 }[/math] is the shape parameter.
The Logistic distribution is recovered as [math]\displaystyle{ \kappa \rightarrow 0. }[/math]
Cumulative distribution function
The cumulative distribution function of κ-Logistic is given by
- [math]\displaystyle{ F_\kappa(x) = \frac{ 1 - \exp_\kappa(-\beta x^\alpha) }{ 1 + (\lambda - 1) \exp_\kappa(-\beta x^\alpha) } }[/math]
valid for [math]\displaystyle{ x \geq 0 }[/math]. The cumulative Logistic distribution is recovered in the classical limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Survival and hazard functions
The survival distribution function of κ-Logistic distribution is given by
- [math]\displaystyle{ S_\kappa(x) = \frac{\lambda}{\exp_\kappa(\beta x^\alpha) + \lambda - 1} }[/math]
valid for [math]\displaystyle{ x \geq 0 }[/math]. The survival Logistic distribution is recovered in the classical limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
The hazard function associated with the κ-Logistic distribution is obtained by the solution of the following evolution equation:
[math]\displaystyle{ \frac{ S_\kappa(x) }{ dx } = -h_\kappa S_\kappa(x) \left( 1 - \frac{ \lambda -1 }{ \lambda } S_\kappa(x) \right) }[/math]
with [math]\displaystyle{ S_\kappa(0) = 1 }[/math], where [math]\displaystyle{ h_\kappa }[/math] is the hazard function:
- [math]\displaystyle{ h_\kappa = \frac{\alpha \beta x^{\alpha-1}}{\sqrt{1+\kappa^2 \beta^2 x^{2\alpha} }} }[/math]
The cumulative Kaniadakis κ-Logistic distribution is related to the hazard function by the following expression:
- [math]\displaystyle{ S_\kappa = e^{-H_\kappa(x)} }[/math]
where [math]\displaystyle{ H_\kappa (x) = \int_0^x h_\kappa(z) dz }[/math] is the cumulative hazard function. The cumulative hazard function of the Logistic distribution is recovered in the classical limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Related distributions
- The survival function of the κ-Logistic distribution represents the κ-deformation of the Fermi-Dirac function, and becomes a Fermi-Dirac distribution in the classical limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].[1]
- The κ-Logistic distribution is a generalization of the κ-Weibull distribution when [math]\displaystyle{ \lambda = 1 }[/math].
- A κ-Logistic distribution corresponds to a Half-Logistic distribution when [math]\displaystyle{ \lambda = 2 }[/math], [math]\displaystyle{ \alpha = 1 }[/math] and [math]\displaystyle{ \kappa = 0 }[/math].
- The ordinary Logistic distribution is a particular case of a κ-Logistic distribution, when [math]\displaystyle{ \kappa = 0 }[/math].
Applications
The κ-Logistic distribution has been applied in several areas, such as:
- In quantum statistics, the survival function of the κ-Logistic distribution represents the most general expression of the Fermi-Dirac function, reducing to the Fermi-Dirac distribution in the limit [math]\displaystyle{ \kappa \rightarrow 0 }[/math].[2][3][4]
See also
- Giorgio Kaniadakis
- Kaniadakis statistics
- Kaniadakis distribution
- Kaniadakis κ-Exponential distribution
- Kaniadakis κ-Gaussian distribution
- Kaniadakis κ-Gamma distribution
- Kaniadakis κ-Weibull distribution
- Kaniadakis κ-Erlang distribution
References
- ↑ 1.0 1.1 1.2 Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters 133 (1): 10002. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. Bibcode: 2021EL....13310002K. https://iopscience.iop.org/article/10.1209/0295-5075/133/10002.
- ↑ Santos, A.P.; Silva, R.; Alcaniz, J.S.; Anselmo, D.H.A.L. (2011). "Kaniadakis statistics and the quantum H-theorem" (in en). Physics Letters A 375 (3): 352–355. doi:10.1016/j.physleta.2010.11.045. Bibcode: 2011PhLA..375..352S.
- ↑ Kaniadakis, G. (2001). "H-theorem and generalized entropies within the framework of nonlinear kinetics" (in en). Physics Letters A 288 (5–6): 283–291. doi:10.1016/S0375-9601(01)00543-6. Bibcode: 2001PhLA..288..283K. https://linkinghub.elsevier.com/retrieve/pii/S0375960101005436.
- ↑ Lourek, Imene; Tribeche, Mouloud (2017). "Thermodynamic properties of the blackbody radiation: A Kaniadakis approach" (in en). Physics Letters A 381 (5): 452–456. doi:10.1016/j.physleta.2016.12.019. Bibcode: 2017PhLA..381..452L. https://linkinghub.elsevier.com/retrieve/pii/S0375960116320060.
External links
 |

