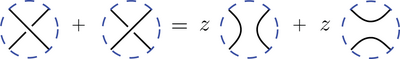Kauffman polynomial
In knot theory, the Kauffman polynomial is a 2-variable knot polynomial due to Louis Kauffman.[1] It is initially defined on a link diagram as
- ,
where is the writhe of the link diagram and is a polynomial in a and z defined on link diagrams by the following properties:
- (O is the unknot).
- L is unchanged under type II and III Reidemeister moves.
Here is a strand and (resp. ) is the same strand with a right-handed (resp. left-handed) curl added (using a type I Reidemeister move).
Additionally L must satisfy Kauffman's skein relation:
The pictures represent the L polynomial of the diagrams which differ inside a disc as shown but are identical outside.
Kauffman showed that L exists and is a regular isotopy invariant of unoriented links. It follows easily that F is an ambient isotopy invariant of oriented links.
The Jones polynomial is a special case of the Kauffman polynomial, as the L polynomial specializes to the bracket polynomial. The Kauffman polynomial is related to Chern–Simons gauge theories for SO(N) in the same way that the HOMFLY polynomial is related to Chern–Simons gauge theories for SU(N).[2]
References
- ↑ Kauffman, Louis (1990). "An invariant of regular isotopy". Transactions of the American Mathematical Society 318 (2): 417–471. doi:10.1090/S0002-9947-1990-0958895-7. http://homepages.math.uic.edu/~kauffman/IRH.pdf.
- ↑ Witten, Edward (1989). "Quantum field theory and the Jones polynomial". Communications in Mathematical Physics 121 (3): 351–399. doi:10.1007/BF01217730. https://projecteuclid.org/euclid.cmp/1104178138.
Further reading
- Kauffman, Louis (1987). On Knots. Annals of Mathematics Studies. 115. Princeton, NJ: Princeton University Press. ISBN 0-691-08435-1.
External links
 |