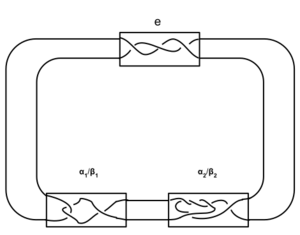
Pretzel link

Short description: Link formed from a finite number of twisted sections

The (−2,3,7) pretzel knot has two right-handed twists in its first tangle, three left-handed twists in its second, and seven left-handed twists in its third.

P(5,3,-2) = T(5,3) = 10₁₂₄

P(3,3,-2) = T(4,3) = 8₁₉

Only two knots are both torus and pretzel

In the mathematical theory of knots, a pretzel link is a special kind of link. It consists of a finite number of tangles made of two intertwined circular helices. The tangles are connected cyclicly, and the first component of the first tangle is connected to the second component of the second tangle, the first component of the second tangle is connected to the second component of the third tangle, and so on. Finally, the first component of the last tangle is connected to the second component of the first. A pretzel link which is also a knot (that is, a link with one component) is a pretzel knot.

Each tangle is characterized by its number of twists: positive if they are counter-clockwise or left-handed, negative if clockwise or right-handed. In the standard projection of the [math]\displaystyle{ (p_1,\,p_2,\dots,\,p_n) }[/math] pretzel link, there are [math]\displaystyle{ p_1 }[/math]left-handed crossings in the first tangle, [math]\displaystyle{ p_2 }[/math]in the second, and, in general, [math]\displaystyle{ p_n }[/math]in the nth.

A pretzel link can also be described as a Montesinos link with integer tangles.

Some basic results

The [math]\displaystyle{ (p_1,p_2,\dots,p_n) }[/math] pretzel link is a knot iff both [math]\displaystyle{ n }[/math] and all the [math]\displaystyle{ p_i }[/math] are odd or exactly one of the [math]\displaystyle{ p_i }[/math] is even.

The [math]\displaystyle{ (p_1,\,p_2,\dots,\,p_n) }[/math] pretzel link is split if at least two of the [math]\displaystyle{ p_i }[/math] are zero; but the converse is false.

The [math]\displaystyle{ (-p_1,-p_2,\dots,-p_n) }[/math] pretzel link is the mirror image of the [math]\displaystyle{ (p_1,\,p_2,\dots,\,p_n) }[/math] pretzel link.

The [math]\displaystyle{ (p_1,\,p_2,\dots,\,p_n) }[/math] pretzel link is isotopic to the [math]\displaystyle{ (p_2,\,p_3,\dots,\,p_n,\,p_1) }[/math] pretzel link. Thus, too, the [math]\displaystyle{ (p_1,\,p_2,\dots,\,p_n) }[/math] pretzel link is isotopic to the [math]\displaystyle{ (p_k,\,p_{k+1},\dots,\,p_n,\,p_1,\,p_2,\dots,\,p_{k-1}) }[/math] pretzel link.

The [math]\displaystyle{ (p_1,\,p_2,\,\dots,\,p_n) }[/math] pretzel link is isotopic to the [math]\displaystyle{ (p_n,\,p_{n-1},\dots,\,p_2,\,p_1) }[/math] pretzel link. However, if one orients the links in a canonical way, then these two links have opposite orientations.

Some examples

The (1, 1, 1) pretzel knot is the (right-handed) trefoil; the (−1, −1, −1) pretzel knot is its mirror image.

The (5, −1, −1) pretzel knot is the stevedore knot (6₁).

If p, q, r are distinct odd integers greater than 1, then the (p, q, r) pretzel knot is a non-invertible knot.

The (2p, 2q, 2r) pretzel link is a link formed by three linked unknots.

The (−3, 0, −3) pretzel knot (square knot (mathematics)) is the connected sum of two trefoil knots.

The (0, q, 0) pretzel link is the split union of an unknot and another knot.

Montesinos

A Montesinos link is a special kind of link that generalizes pretzel links (a pretzel link can also be described as a Montesinos link with integer tangles). A Montesinos link which is also a knot (i.e., a link with one component) is a Montesinos knot.

A Montesinos link is composed of several rational tangles. One notation for a Montesinos link is [math]\displaystyle{ K(e;\alpha_1 /\beta_1,\alpha_2 /\beta_2,\ldots,\alpha_n /\beta_n) }[/math].

In this notation, [math]\displaystyle{ e }[/math] and all the [math]\displaystyle{ \alpha_i }[/math] and [math]\displaystyle{ \beta_i }[/math] are integers. The Montesinos link given by this notation consists of the sum of the rational tangles given by the integer [math]\displaystyle{ e }[/math] and the rational tangles [math]\displaystyle{ \alpha_1 /\beta_1,\alpha_2 /\beta_2,\ldots,\alpha_n /\beta_n }[/math]

These knots and links are named after the Spanish topologist José María Montesinos Amilibia, who first introduced them in 1973.

Utility

(−2, 3, 2n + 1) pretzel links are especially useful in the study of 3-manifolds. Many results have been stated about the manifolds that result from Dehn surgery on the (−2,3,7) pretzel knot in particular.

The hyperbolic volume of the complement of the (−2,3,8) pretzel link is 4 times Catalan's constant, approximately 3.66. This pretzel link complement is one of two two-cusped hyperbolic manifolds with the minimum possible volume, the other being the complement of the Whitehead link.

A Montesinos link. In this example, [math]\displaystyle{ e=-3 }[/math] , [math]\displaystyle{ \alpha_1 /\beta_1=-3/2 }[/math] and [math]\displaystyle{ \alpha_2 /\beta_2=5/2 }[/math].

Edible (−2,3,7) pretzel knot

Another edible (–2,3,7) pretzel knot, glazed to perfection

Further reading

• Trotter, Hale F.: Non-invertible knots exist, Topology, 2 (1963), 272–280.
• Burde, Gerhard; Zieschang, Heiner (2003). Knots. De Gruyter studies in mathematics. 5 (2nd revised and extended ed.). Walter de Gruyter. ISBN 3110170051.