Level-set method

From HandWiki
Short description: Conceptual framework used in numerical analysis of surfaces and shapes


File:Levelset-mean-curvature-spiral.ogv Level-set methods (LSM) constitute a conceptual framework for using level sets as a tool for the numerical analysis of surfaces and shapes. Invented in 1988 by Osher and Sethian, the key advantage of LSM is its ability to perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects (this is called the Eulerian approach).[1] Importantly, LSM makes it easier to follow shapes with sharp corners or that change topology, for example, when a shape splits in two, develops holes, or the reverse of these operations. These characteristics make LSM an effective method for modeling time-varying objects, like inflation of an airbag, or a drop of oil floating in water.

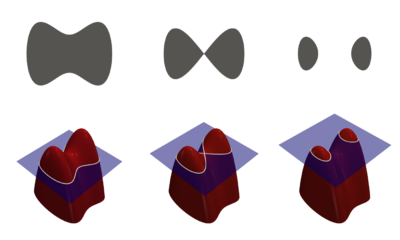
An illustration of the level-set method

The figure on the right illustrates several ideas about LSM. In the upper-left corner we see a shape; that is, a bounded region with a well-behaved boundary. Below it, the red surface is the graph of a level set function [math]\displaystyle{ \varphi }[/math] determining this shape, and the flat blue region represents the X-Y plane. The boundary of the shape is then the zero-level set of [math]\displaystyle{ \varphi }[/math], while the shape itself is the set of points in the plane for which [math]\displaystyle{ \varphi }[/math] is positive (interior of the shape) or zero (at the boundary).

In the top row, the shape can be seen changing its topology by splitting in two. It would be difficult to describe this transformation numerically by parameterizing the boundary of the shape and following its evolution. One would need an algorithm to be able to detect the moment the shape splits in two and then construct parameterizations for the two newly obtained curves. On the bottom row, however, the level set function accomplishes this change by translating downward. This is an example of when it can be easier to work with a shape through its level-set function than with the shape directly, where the method would need to consider and handle all the possible deformations the shape might undergo.

Thus, in two dimensions, the level-set method amounts to representing a closed curve [math]\displaystyle{ \Gamma }[/math] (such as the shape boundary in our example) using an auxiliary function [math]\displaystyle{ \varphi }[/math], called the level-set function. The curve [math]\displaystyle{ \Gamma }[/math] is represented as the zero-level set of [math]\displaystyle{ \varphi }[/math] by

[math]\displaystyle{ \Gamma = \{(x, y) \mid \varphi(x, y) = 0 \}, }[/math]

and the level-set method manipulates [math]\displaystyle{ \Gamma }[/math] implicitly through the function [math]\displaystyle{ \varphi }[/math]. This function [math]\displaystyle{ \varphi }[/math] is assumed to take positive values inside the region delimited by the curve [math]\displaystyle{ \Gamma }[/math] and negative values outside.[2][3]

The level-set equation

If the curve [math]\displaystyle{ \Gamma }[/math] moves in the normal direction with a speed [math]\displaystyle{ v }[/math], then by chain rule and implicit differentiation, we get that the level-set function [math]\displaystyle{ \varphi }[/math] satisfies the level-set equation

[math]\displaystyle{ \frac{\partial\varphi}{\partial t} = v|\nabla \varphi|. }[/math]

Here, [math]\displaystyle{ |\cdot| }[/math] is the Euclidean norm (denoted customarily by single bars in partial differential equations), and [math]\displaystyle{ t }[/math] is time. This is a partial differential equation, in particular a Hamilton–Jacobi equation, and can be solved numerically, for example, by using finite differences on a Cartesian grid.[2][3]

However, numerical solution of the level set equation may require complex techniques. Simple finite difference methods fail quickly. Upwinding methods such as the Godunov method are considered better; however, the level set method does not guarantee preservation of the volume and shape of the set level in an advection field that maintains shape and size, for example a uniform or rotational velocity field. Instead, the shape of the level set may become distorted and the level set may disappear over a few time steps. Therefore, high-order finite difference schemes, such as high-order essentially non-oscillatory (ENO) schemes, are often required, and even then the feasibility of long-term simulations is questionable. More complex methods have been developed to overcome this; for example, combinations of the leveling method with tracking marker particles suggested by the velocity field.[4]

Example

Consider a unit circle in [math]\displaystyle{ \mathbb{R}^2 }[/math], shrinking in on itself at a constant rate, i.e. each point on the boundary of the circle moves along its inwards pointing normal at some fixed speed. The circle will shrink and eventually collapse down to a point. If an initial distance field is constructed (i.e. a function whose value is the signed Euclidean distance to the boundary, positive interior, negative exterior) on the initial circle, the normalized gradient of this field will be the circle normal.

If the field has a constant value subtracted from it in time, the zero level (which was the initial boundary) of the new fields will also be circular and will similarly collapse to a point. This is due to this being effectively the temporal integration of the Eikonal equation with a fixed front velocity.

In combustion, this method is used to describe the instantaneous flame surface, known as the G equation.

History

The level-set method was developed in 1979 by Alain Dervieux,[5] and subsequently popularized by Stanley Osher and James Sethian. It has become popular in many disciplines, such as image processing, computer graphics, computational geometry, optimization, computational fluid dynamics, and computational biology.

A number of level-set data structures have been developed to facilitate the use of the level-set method in computer applications.

Applications

See also


References

  1. ↑ Osher, S.; Sethian, J. A. (1988), "Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations", J. Comput. Phys. 79 (1): 12–49, doi:10.1016/0021-9991(88)90002-2, Bibcode: 1988JCoPh..79...12O, http://math.berkeley.edu/~sethian/Papers/sethian.osher.88.pdf 
  2. ↑ 2.0 2.1 Osher, Stanley J.; Fedkiw, Ronald P. (2002). Level Set Methods and Dynamic Implicit Surfaces. Springer-Verlag. ISBN 978-0-387-95482-0. 
  3. ↑ 3.0 3.1 Sethian, James A. (1999). Level Set Methods and Fast Marching Methods : Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge University Press. ISBN 978-0-521-64557-7. 
  4. ↑ Enright, D.; Fedkiw, R. P.; Ferziger, J. H.; Mitchell, I. (2002), "A hybrid particle level set method for improved interface capturing", J. Comput. Phys. 183 (1): 83–116, doi:10.1006/jcph.2002.7166, Bibcode: 2002JCoPh.183...83E, http://www.cs.ubc.ca/~mitchell/Papers/myJCP02.pdf 
  5. ↑ Dervieux, A.; Thomasset, F. (1980). "A finite element method for the simulation of a Rayleigh-Taylor instability". Approximation Methods for Navier-Stokes Problems. Lecture Notes in Mathematics. 771. Springer. pp. 145–158. doi:10.1007/BFb0086904. ISBN 978-3-540-38550-9. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Level-set_method&oldid=3386959"