Linear separability
In Euclidean geometry, linear separability is a property of two sets of points. This is most easily visualized in two dimensions (the Euclidean plane) by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are linearly separable if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if the line is replaced by a hyperplane.
The problem of determining if a pair of sets is linearly separable and finding a separating hyperplane if they are, arises in several areas. In statistics and machine learning, classifying certain types of data is a problem for which good algorithms exist that are based on this concept.
Mathematical definition
Let [math]\displaystyle{ X_{0} }[/math] and [math]\displaystyle{ X_{1} }[/math] be two sets of points in an n-dimensional Euclidean space. Then [math]\displaystyle{ X_{0} }[/math] and [math]\displaystyle{ X_{1} }[/math] are linearly separable if there exist n + 1 real numbers [math]\displaystyle{ w_{1}, w_{2},..,w_{n}, k }[/math], such that every point [math]\displaystyle{ x \in X_{0} }[/math] satisfies [math]\displaystyle{ \sum^{n}_{i=1} w_{i}x_{i} \gt k }[/math] and every point [math]\displaystyle{ x \in X_{1} }[/math] satisfies [math]\displaystyle{ \sum^{n}_{i=1} w_{i}x_{i} \lt k }[/math], where [math]\displaystyle{ x_{i} }[/math] is the [math]\displaystyle{ i }[/math]-th component of [math]\displaystyle{ x }[/math].
Equivalently, two sets are linearly separable precisely when their respective convex hulls are disjoint (colloquially, do not overlap).[1]
In simple 2D, it can also be imagined that the set of points under a linear transformation collapses into a line, on which there exists a value, k, greater than which one set of points will fall into, and lesser than which the other set of points fall.
Examples
Three non-collinear points in two classes ('+' and '-') are always linearly separable in two dimensions. This is illustrated by the three examples in the following figure (the all '+' case is not shown, but is similar to the all '-' case):
|
|
|
However, not all sets of four points, no three collinear, are linearly separable in two dimensions. The following example would need two straight lines and thus is not linearly separable:
|
Notice that three points which are collinear and of the form "+ ⋅⋅⋅ — ⋅⋅⋅ +" are also not linearly separable.
Number of linear separations
Let [math]\displaystyle{ T(N, K) }[/math] be the number of ways to linearly separate N points (in general position) in K dimensions, then[2][math]\displaystyle{ T(N, K)=\left\{\begin{array}{cc} 2^N & K \geq N \\ 2 \sum_{k=0}^{K-1}\left(\begin{array}{c} N-1 \\ k \end{array}\right) & K\lt N \end{array}\right. }[/math]When K is large, [math]\displaystyle{ T(N, K)/2^N }[/math] is very close to one when [math]\displaystyle{ N \leq 2K }[/math], but very close to zero when [math]\displaystyle{ N\gt 2K }[/math]. In words, one perceptron unit can almost certainly memorize a random assignment of binary labels on N points when [math]\displaystyle{ N \leq 2K }[/math], but almost certainly not when [math]\displaystyle{ N\gt 2K }[/math].
Linear separability of Boolean functions in n variables
A Boolean function in n variables can be thought of as an assignment of 0 or 1 to each vertex of a Boolean hypercube in n dimensions. This gives a natural division of the vertices into two sets. The Boolean function is said to be linearly separable provided these two sets of points are linearly separable. The number of distinct Boolean functions is [math]\displaystyle{ 2^{2^{n}} }[/math]where n is the number of variables passed into the function.[3]
Such functions are also called linear threshold logic, or perceptrons. The classical theory is summarized in,[4] as Knuth claims.[5]
The value is only known exactly up to [math]\displaystyle{ n=9 }[/math] case, but the order of magnitude is known quite exactly: it has upper bound [math]\displaystyle{ 2^{n^2 - n \log_2 n + O(n)} }[/math] and lower bound [math]\displaystyle{ 2^{n^2 - n \log_2 n - O(n)} }[/math].[6]
It is co-NP-complete to decide whether a Boolean function given in disjunctive or conjunctive normal form is linearly separable.[6]
| Number of variables | Boolean functions | Linearly separable Boolean functions |
|---|---|---|
| 2 | 16 | 14 |
| 3 | 256 | 104 |
| 4 | 65536 | 1882 |
| 5 | 4294967296 | 94572 |
| 6 | 18446744073709552000 | 15028134 |
| 7 | 3.402823669 ×10^38 | 8378070864 |
| 8 | 1.157920892 ×10^77 | 17561539552946 |
| 9 | 1.340780792 ×10^154 | 144130531453121108 |
Support vector machines
.svg)
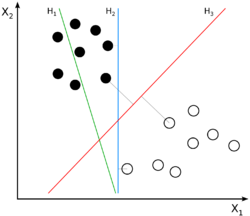
Classifying data is a common task in machine learning. Suppose some data points, each belonging to one of two sets, are given and we wish to create a model that will decide which set a new data point will be in. In the case of support vector machines, a data point is viewed as a p-dimensional vector (a list of p numbers), and we want to know whether we can separate such points with a (p − 1)-dimensional hyperplane. This is called a linear classifier. There are many hyperplanes that might classify (separate) the data. One reasonable choice as the best hyperplane is the one that represents the largest separation, or margin, between the two sets. So we choose the hyperplane so that the distance from it to the nearest data point on each side is maximized. If such a hyperplane exists, it is known as the maximum-margin hyperplane and the linear classifier it defines is known as a maximum margin classifier.
More formally, given some training data [math]\displaystyle{ \mathcal{D} }[/math], a set of n points of the form
- [math]\displaystyle{ \mathcal{D} = \left\{ (\mathbf{x}_i, y_i)\mid\mathbf{x}_i \in \mathbb{R}^p,\, y_i \in \{-1,1\}\right\}_{i=1}^n }[/math]
where the yi is either 1 or −1, indicating the set to which the point [math]\displaystyle{ \mathbf{x}_i }[/math] belongs. Each [math]\displaystyle{ \mathbf{x}_i }[/math] is a p-dimensional real vector. We want to find the maximum-margin hyperplane that divides the points having [math]\displaystyle{ y_i=1 }[/math] from those having [math]\displaystyle{ y_i=-1 }[/math]. Any hyperplane can be written as the set of points [math]\displaystyle{ \mathbf{x} }[/math] satisfying
- [math]\displaystyle{ \mathbf{w}\cdot\mathbf{x} - b=0, }[/math]
where [math]\displaystyle{ \cdot }[/math] denotes the dot product and [math]\displaystyle{ {\mathbf{w}} }[/math] the (not necessarily normalized) normal vector to the hyperplane. The parameter [math]\displaystyle{ \tfrac{b}{\|\mathbf{w}\|} }[/math] determines the offset of the hyperplane from the origin along the normal vector [math]\displaystyle{ {\mathbf{w}} }[/math].
If the training data are linearly separable, we can select two hyperplanes in such a way that they separate the data and there are no points between them, and then try to maximize their distance.
See also
- Clustering (statistics)
- Hyperplane separation theorem
- Kirchberger's theorem
- Perceptron
- Vapnik–Chervonenkis dimension
References
- ↑ Boyd, Stephen; Vandenberghe, Lieven (2004-03-08). Convex Optimization. Cambridge University Press. doi:10.1017/cbo9780511804441. ISBN 978-0-521-83378-3. http://dx.doi.org/10.1017/cbo9780511804441.
- ↑ MacKay, David (2003-09-25). Information Theory, Inference and Learning Algorithms. Cambridge University Press. p. 483. ISBN 9780521642989. https://books.google.com/books?id=AKuMj4PN_EMC&pg=PA483.
- ↑ Russell, Stuart J. (2016). Artificial intelligence a modern approach. Norvig, Peter 1956- (Third ed.). Boston. pp. 766. ISBN 978-1292153964. OCLC 945899984.
- ↑ Muroga, Saburo (1971). Threshold logic and its applications. New York: Wiley-Interscience. ISBN 978-0-471-62530-8.
- ↑ Knuth, Donald Ervin (2011). The art of computer programming. Upper Saddle River: Addison-Wesley. pp. 75–79. ISBN 978-0-201-03804-0.
- ↑ 6.0 6.1 Šíma, Jiří; Orponen, Pekka (2003-12-01). "General-Purpose Computation with Neural Networks: A Survey of Complexity Theoretic Results" (in en). Neural Computation 15 (12): 2727–2778. doi:10.1162/089976603322518731. ISSN 0899-7667. PMID 14629867. https://direct.mit.edu/neco/article/15/12/2727-2778/6791.
- ↑ Gruzling, Nicolle (2006). Linear separability of the vertices of an n-dimensional hypercube. M.Sc Thesis. University of Northern British Columbia.
 |  |
