Disjunctive normal form
In boolean logic, a disjunctive normal form (DNF) is a canonical normal form of a logical formula consisting of a disjunction of conjunctions; it can also be described as an OR of ANDs, a sum of products, or — in philosophical logic — a cluster concept.[1] As a normal form, it is useful in automated theorem proving.
Definition
A logical formula is considered to be in DNF if it is a disjunction of one or more conjunctions of one or more literals.[2][3][4] A DNF formula is in full disjunctive normal form if each of its variables appears exactly once in every conjunction and each conjunction appears at most once (up to the order of variables). As in conjunctive normal form (CNF), the only propositional operators in DNF are and ([math]\displaystyle{ \wedge }[/math]), or ([math]\displaystyle{ \vee }[/math]), and not ([math]\displaystyle{ \neg }[/math]). The not operator can only be used as part of a literal, which means that it can only precede a propositional variable.
The following is a context-free grammar for DNF:
- DNF → (Conjunction) [math]\displaystyle{ \vee }[/math] DNF
- DNF → (Conjunction)
- Conjunction → Literal [math]\displaystyle{ \wedge }[/math] Conjunction
- Conjunction → Literal
- Literal → [math]\displaystyle{ \neg }[/math]Variable
- Literal → Variable
Where Variable is any variable.
For example, all of the following formulas are in DNF:
- [math]\displaystyle{ (A \land \neg B \land \neg C) \lor (\neg D \land E \land F \land D \land F) }[/math]
- [math]\displaystyle{ (A \land B) \lor (C) }[/math]
- [math]\displaystyle{ (A \land B) }[/math]
- [math]\displaystyle{ (A) }[/math]
The formula [math]\displaystyle{ A \lor B }[/math] is in DNF, but not in full DNF; an equivalent full-DNF version is [math]\displaystyle{ (A \land B) \lor (A \land \lnot B) \lor (\lnot A \land B) }[/math].
The following formulas are not in DNF:[5]
- [math]\displaystyle{ \neg(A \lor B) }[/math], since an OR is nested within a NOT
- [math]\displaystyle{ \neg(A \land B) \lor C }[/math], since an AND is nested within a NOT
- [math]\displaystyle{ A \lor (B \land (C \lor D)) }[/math], since an OR is nested within an AND
Conversion to DNF
In classical logic each propositional formula can be converted to DNF[6] ...
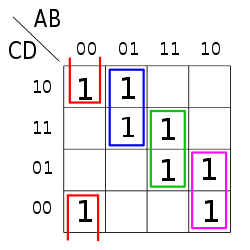
... by syntactic means
The conversion involves using logical equivalences, such as double negation elimination, De Morgan's laws, and the distributive law. Formulas built from the primitive connectives [math]\displaystyle{ \{\land,\lor,\lnot\} }[/math][7] can be converted to DNF by the following canonical term rewriting system:[8]
- [math]\displaystyle{ \begin{array}{rcl} (\lnot \lnot x) & \rightsquigarrow & x \\ (\lnot (x \lor y)) & \rightsquigarrow & ((\lnot x) \land (\lnot y)) \\ (\lnot (x \land y)) & \rightsquigarrow & ((\lnot x) \lor (\lnot y)) \\ (x \land (y \lor z)) & \rightsquigarrow & ((x \land y) \lor (x \land z)) \\ ((x \lor y) \land z) & \rightsquigarrow & ((x \land z) \lor (y \land z)) \\ \end{array} }[/math]
... by semantic means
The full DNF of a formula can be read off its truth table.[9] For example, consider the formula
- [math]\displaystyle{ \phi = ((\lnot (p \land q)) \leftrightarrow (\lnot r \uparrow (p \oplus q))) }[/math].[10]
The corresponding truth table is
[math]\displaystyle{ p }[/math] [math]\displaystyle{ q }[/math] [math]\displaystyle{ r }[/math] [math]\displaystyle{ ( }[/math] [math]\displaystyle{ \lnot }[/math] [math]\displaystyle{ (p \land q) }[/math] [math]\displaystyle{ ) }[/math] [math]\displaystyle{ \leftrightarrow }[/math] [math]\displaystyle{ ( }[/math] [math]\displaystyle{ \lnot r }[/math] [math]\displaystyle{ \uparrow }[/math] [math]\displaystyle{ (p \oplus q) }[/math] [math]\displaystyle{ ) }[/math] T T T F T F F T F T T F F T F T T F T F T T F T F T T T F F T F F T F T F T T T F T F T T F T F T F F T F T F F T T F T F T F F F F T F T T T F
- The full DNF equivalent of [math]\displaystyle{ \phi }[/math] is
- [math]\displaystyle{ ( p \land \lnot q \land r) \lor (\lnot p \land q \land r) \lor (\lnot p \land \lnot q \land r) \lor (\lnot p \land \lnot q \land \lnot r) }[/math]
- The full DNF equivalent of [math]\displaystyle{ \lnot \phi }[/math] is
- [math]\displaystyle{ ( p \land q \land r) \lor ( p \land q \land \lnot r) \lor ( p \land \lnot q \land \lnot r) \lor (\lnot p \land q \land \lnot r) }[/math]
Remark
A propositional formula can be represented by one and only one full DNF.[12] In contrast, several plain DNFs may be possible. For example, by applying the rule [math]\displaystyle{ ((a \land b) \lor (\lnot a \land b)) \rightsquigarrow b }[/math] three times, the full DNF of the above [math]\displaystyle{ \phi }[/math] can be simplified to [math]\displaystyle{ (\lnot p \land \lnot q) \lor (\lnot p \land r) \lor (\lnot q \land r) }[/math]. However, there are also equivalent DNF formulas that cannot be transformed one into another by this rule, see the pictures for an example.
Maximum number of conjunctions
Any propositional formula is built from [math]\displaystyle{ n }[/math] variables, where [math]\displaystyle{ n \ge 1 }[/math].
There are [math]\displaystyle{ 2n }[/math] possible literals: [math]\displaystyle{ L = \{ p_1, \lnot p_1, p_2, \lnot p_2, \ldots, p_n, \lnot p_n\} }[/math].
[math]\displaystyle{ L }[/math] has [math]\displaystyle{ (2^{2n} -1) }[/math] non-empty subsets.[13]
This is the maximum number of conjunctions a DNF can have.[12]
A full DNF can have up to [math]\displaystyle{ 2^{n} }[/math] conjunctions, one for each row of the truth table.
Example 1
Consider a formula with two variables [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math].
The longest possible DNF has [math]\displaystyle{ 2^{(2 \times 2)} -1 = 15 }[/math] conjunctions:[12]
- [math]\displaystyle{ \begin{array}{lcl} (\lnot p) \lor (p) \lor (\lnot q) \lor (q) \lor \\ (\lnot p \land p) \lor \underline{(\lnot p \land \lnot q)} \lor \underline{(\lnot p \land q)} \lor \underline{( p \land \lnot q)} \lor \underline{( p \land q)} \lor (\lnot q \land q) \lor \\ (\lnot p \land p \land \lnot q) \lor (\lnot p \land p \land q) \lor (\lnot p \land \lnot q \land q) \lor ( p \land \lnot q \land q) \lor \\ (\lnot p \land p \land \lnot q \land q) \end{array} }[/math]
The longest possible full DNF has 4 conjunctions: they are underlined.
This formula is a tautology.
Example 2
Each DNF of the e.g. formula [math]\displaystyle{ (X_1 \lor Y_1) \land (X_2 \lor Y_2) \land \dots \land (X_n \lor Y_n) }[/math] has [math]\displaystyle{ 2^n }[/math] conjunctions.
Computational complexity
The Boolean satisfiability problem on conjunctive normal form formulas is NP-complete. By the duality principle, so is the falsifiability problem on DNF formulas. Therefore, it is co-NP-hard to decide if a DNF formula is a tautology.
Conversely, a DNF formula is satisfiable if, and only if, one of its conjunctions is satisfiable. This can be decided in polynomial time.[14]
Variants
An important variation used in the study of computational complexity is k-DNF. A formula is in k-DNF if it is in DNF and each conjunction contains at most k literals.[15]
See also
- Algebraic normal form – an XOR of AND clauses
- Blake canonical form – DNF including all prime implicants
- Quine–McCluskey algorithm – algorithm for calculating prime implicants
- Propositional logic
- Truth table
Notes
- ↑ Post 1921.
- ↑ Davey & Priestley 1990, p. 153.
- ↑ Gries & Schneider 1993, p. 67.
- ↑ Whitesitt 2012, pp. 33-37.
- ↑ However, they are in negation normal form.
- ↑ Davey & Priestley 1990, p. 152-153.
- ↑ Formulas with other connectives can be brought into negation normal form first.
- ↑ Dershowitz & Jouannaud 1990, p. 270, Sect.5.1.
- ↑ Sobolev 2020.
- ↑ [math]\displaystyle{ \phi }[/math] = ((NOT (p AND q)) IFF ((NOT r) NAND (p XOR q)))
- ↑ like [math]\displaystyle{ (a \land b) \lor (b \land a) \lor (a \land b \land b) }[/math]
- ↑ 12.0 12.1 12.2 It is assumed that repetitions and variations[11] based on the commutativity and associativity of [math]\displaystyle{ \lor }[/math] and [math]\displaystyle{ \land }[/math] do not occur.
- ↑ [math]\displaystyle{ \left|\mathcal{P}(L)\right| = 2^{2n} }[/math]
- ↑ Zimmermann 2015.
- ↑ Arora & Barak 2009.
References
- Arora, Sanjeev; Barak, Boaz (20 April 2009). Computational Complexity: A Modern Approach. Cambridge University Press. pp. 579. doi:10.1017/CBO9780511804090. ISBN 9780521424264.
- Davey, B.A.; Priestley, H.A. (1990). Introduction to Lattices and Order. Cambridge Mathematical Textbooks. Cambridge University Press.
- Dershowitz, Nachum; Jouannaud, Jean-Pierre (1990). "Rewrite Systems". in Van Leeuwen, Jan. Formal Models and Semantics. Handbook of Theoretical Computer Science. B. Elsevier. pp. 243–320. ISBN 0-444-88074-7.
- Gries, David; Schneider, Fred B. (22 October 1993). A Logical Approach to Discrete Math. Springer Science & Business Media. ISBN 978-0-387-94115-8. https://books.google.com/books?id=ZWTDQ6H6gsUC&q=%22disjunctive+normal+form%22&pg=PA67.
- Hilbert, David; Ackermann, Wilhelm (1999). Principles of Mathematical Logic. American Mathematical Soc.. ISBN 978-0-8218-2024-7. https://books.google.com/books?id=45ZGMjV9vfcC&q=%22disjunctive+normal+form%22.
- Howson, Colin (11 October 2005). Logic with trees: an introduction to symbolic logic. Routledge. ISBN 978-1-134-78550-6. https://books.google.com/books?id=Y4WGAgAAQBAJ&q=%22disjunctive+normal+form%22.
- Post, Emil (July 1921). "Introduction to a General Theory of Elementary Propositions". American Journal of Mathematics 43 (3): 163-185. doi:10.2307/2370324.
- Hazewinkel, Michiel, ed. (2001), "Disjunctive normal form", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page
- Whitesitt, J. Eldon (24 May 2012). Boolean Algebra and Its Applications. Courier Corporation. ISBN 978-0-486-15816-7. https://books.google.com/books?id=20Un1T78GlMC&q=%22disjunctive+normal+form%22.
- Zimmermann, Martin (2015-01-22). "The Complexity of Counting Models of Linear-time Temporal Logic". Saarland University. https://www.react.uni-saarland.de/people/zimmermann/slides/AlgoSyn_2015.pdf.
 |  |
