Lugiato–Lefever equation

From HandWiki

The numerical models of lasers and the most of nonlinear optical systems stem from Maxwell–Bloch equations (MBE). This full set of Partial Differential Equations includes Maxwell equations for electromagnetic field and semiclassical equations of the two-level (or multilevel) atoms. For this reason the simplified theoretical approaches were developed for numerical simulation of laser beams formation and their propagation since the early years of laser era.[1] The Slowly varying envelope approximation of MBE follows from the standard nonlinear wave equation with nonlinear polarization [math]\displaystyle{ \mathbf{P}^\text{NL} }[/math] as a source:[2]

[math]\displaystyle{ \nabla^2 {\cal E(\vec r,t)}- \frac{n^2}{c^2}\frac{\partial^2}{\partial t^2} {\cal E(\vec r,t)} = \frac{1}{\varepsilon_0 c^2}\frac{\partial^2}{\partial t^2}\mathbf{P}^\text{NL}, }[/math] where :[math]\displaystyle{ {\cal E}(\vec r,t)\propto E(\vec r_\perp,z,t)e^{i(n k_0)(z-ct)} + \text{c.c.} }[/math]

resulting in the standard "parabolic" wave equation:

[math]\displaystyle{ \frac{\partial E}{\partial z} + \frac{\; \omega_0\ }{ k_0 c^2} \frac{\partial E}{\partial t} - \tfrac{1}{2 k_0 }\ i\ \nabla^2_\perp E = \frac{1}{\varepsilon_0 k_0 c^2}\frac{\partial^2}{\partial t^2}\mathbf{P}^\text{NL}~ }[/math], under conditions :

[math]\displaystyle{ \displaystyle \left|\ \nabla^2 E\ \right| \ll \left|\ k_0 \nabla E\ \right| }[/math]   and   [math]\displaystyle{ \displaystyle \left|\ \frac{\partial^2 E}{\partial t^2}\ \right| \ll \left|\ \omega_0\, \frac{\partial E}{\partial t}\ \right|\ }[/math] .

The averaging over longitudinal coordinate [math]\displaystyle{ z }[/math] results in "mean-field" Suchkov-Letokhov equation (SLE) describing the nonstationary evolution of the transverse mode pattern.[3]

The model usually designated as Lugiato–Lefever equation (LLE) was formulated in 1987 by Luigi Lugiato and René Lefever [4] as a paradigm for spontaneous pattern formation in nonlinear optical systems.[5][6][7] The patterns originate from the interaction of a coherent field, that is injected into a resonant optical cavity, with a Kerr medium that fills the cavity.

The same equation governs two types of patterns: stationary patterns that arise in the planes orthogonal with respect to the direction of propagation of light (transverse patterns) and patterns that form in the longitudinal direction (longitudinal patterns), travel along the cavity with the velocity of light in the medium and give rise to a sequence of pulses in the output of the cavity.

The case of longitudinal patterns is intrinsically linked to the phenomenon of “Kerr frequency combs” in microresonators, discovered in 2007 by Tobias Kippenberg and collaborators,[8] that has raised a very lively interest, especially because of the applicative avenue it has opened.

The LLE equation

Figure 1 shows a light beam that propagates in the [math]\displaystyle{ z }[/math] direction, while [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are the transverse directions. If we assume that the electric field as [math]\displaystyle{ {\cal E}(x,y,z,t) }[/math], where [math]\displaystyle{ t }[/math] denotes time, is linearly polarized and therefore can be treated as a scalar, we can express it in terms of the slowly varying normalized complex envelope [math]\displaystyle{ E(x,y,z,t) }[/math] in this way

Figure 1. A light beam propagates along the [math]\displaystyle{ z }[/math] direction. [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are the transverse directions
[math]\displaystyle{ {\cal E}(x,y,z,t)\propto E(x,y,z,t)e^{i(\omega_0/\tilde{c})(z-\tilde{c}t)} + \text{c.c.} }[/math]

where [math]\displaystyle{ \omega_0 }[/math] is the frequency of the light beam that is injected into the cavity and [math]\displaystyle{ \tilde{c} }[/math] of the light velocity in the Kerr medium that fills the cavity. For definiteness, consider a ring cavity (Fig. 2) of very high quality (High-Q cavity).

Figure 2. Top view of ring cavity

In the original LLE,[4] one assumes conditions such that the envelope [math]\displaystyle{ E }[/math] is independent of the longitudinal variable [math]\displaystyle{ z }[/math] (i.e. uniform along the cavity), so that [math]\displaystyle{ E=E(x,y,t) }[/math]. The equation reads

[math]\displaystyle{ \frac{\partial E}{\partial \bar{t}}=E_\text{in}-E-i\theta E+i|E|^2 E+i\nabla^2_\perp E }[/math]

 

 

 

 

(1)

[math]\displaystyle{ \nabla^2_\perp E=\frac{\partial^2E}{\partial \bar{x}^2}+\frac{\partial^2E}{\partial \bar{y}^2} }[/math]

where [math]\displaystyle{ \bar{t} }[/math] and [math]\displaystyle{ \bar{x} }[/math], [math]\displaystyle{ \bar{y} }[/math] are normalized temporal and spatial variables, i.e. [math]\displaystyle{ \bar{t}=\kappa t }[/math], [math]\displaystyle{ \bar{x}=x/\ell_d }[/math], [math]\displaystyle{ \bar{y}=y/\ell_d }[/math], with [math]\displaystyle{ \kappa }[/math] being the cavity decay rate or cavity linewidth, [math]\displaystyle{ \ell_d }[/math] the diffraction length in the cavity. [math]\displaystyle{ \theta=(\omega_c-\omega_0)/\kappa }[/math] is the cavity detuning parameter, with [math]\displaystyle{ \omega_c }[/math] being the cavity frequency nearest to [math]\displaystyle{ \omega_0 }[/math]. In the righthand side of Eq.(1), [math]\displaystyle{ E_\text{in} }[/math] is the normalized amplitude of the input field that is injected into the cavity, the second is the decay term, the third is the detuning term, the fourth is the cubic nonlinear term that takes into account the Kerr medium, the last term with the transverse Laplacian [math]\displaystyle{ \nabla_\perp^2 }[/math] describes diffraction in the paraxial approximation. Conditions of self-focusing are assumed.

We refer to Eq.(1) as the transverse LLE. Some years later than,[4] there was the formulation of the longitudinal LLE, in which diffraction is replaced by dispersion.[9][10] In this case one assumes that the envelope [math]\displaystyle{ E }[/math] is independent of the transverse variables [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math], so that [math]\displaystyle{ E=E(z,t) }[/math]. The longitudinal LLE reads

[math]\displaystyle{ \frac{\partial E}{\partial \bar{t}}=E_\text{in}-E-i\theta E+i|E|^2 E+i\frac{\partial^2 E}{\partial\bar{z}^2} }[/math]

 

 

 

 

(2)

with [math]\displaystyle{ \bar{z}=z/a }[/math], where [math]\displaystyle{ a }[/math] depends, in particular on the dispersion parameter at second order. Conditions of anomalous dispersion are assumed. An important point is that, once [math]\displaystyle{ E(\bar{z},\bar{t}) }[/math] is obtained by solving Eq.(2), one must come back to the original variables [math]\displaystyle{ z,t }[/math] and replace [math]\displaystyle{ z }[/math] by [math]\displaystyle{ z-\tilde{c}t }[/math], so that a [math]\displaystyle{ z }[/math]-dependent stationary solution (stationary pattern) becomes a travelling pattern (with velocity [math]\displaystyle{ \tilde{c} }[/math]).

From a mathematical viewpoint, the LLE amounts to a driven, damped, detuned nonlinear Schroedinger equation.

The transverse LLE (1) is in 2D from the spatial viewpoint. In a waveguide configuration [math]\displaystyle{ E }[/math] depends only on one spatial variable, say [math]\displaystyle{ x }[/math], and the transverse Laplacian is replaced by [math]\displaystyle{ \frac{\partial^2 E}{\partial \bar{x}^2} }[/math] and one has the transverse LLE in 1D. The longitudinal LLE (2) is equivalent to the transverse LLE in 1D.

In some papers dealing with the longitudinal case one considers dispersion beyond the second order, so that Eq.(2) includes also terms with derivatives of order higher than second with respect to [math]\displaystyle{ \bar{z} }[/math].

Uniform stationary solutions. Connection with optical bistability. Four-wave mixing and pattern formation.

Figure 3. Stationary curve of the normalized output intensity [math]\displaystyle{ |E|^2 }[/math] as a function of the normalized input intensity [math]\displaystyle{ |E_\text{in}|^2 }[/math] for [math]\displaystyle{ \theta=4 }[/math]. The stationary states in the segment with negative slope are unstable. The arrows show the hysteresis cycle which is covered when [math]\displaystyle{ |E_\text{in}|^2 }[/math] is increased and then decreased.

Let us focus on the case in which the envelope [math]\displaystyle{ E }[/math] is constant, i.e. on the stationary solutions that are independent of all spatial variables. By dropping all derivatives in Eqs.(1) and (2), and taking the squared modulus, one obtains the stationary equation

[math]\displaystyle{ |E_\text{in}|^2=|E|^2\left\{1+(\theta-|E|^2)^2\right\} }[/math]

 

 

 

 

(3)

If we plot the stationary curve of [math]\displaystyle{ |E|^2 }[/math] as a function of [math]\displaystyle{ |E_\text{in}|^2 }[/math], when [math]\displaystyle{ \theta\gt \sqrt{3} }[/math] we obtain a curve as that shown in Fig.3.

The curve is [math]\displaystyle{ S }[/math]-shaped and there is an interval of values of [math]\displaystyle{ |E_\text{in}|^2 }[/math] where one has three stationary states. However, the states that lie in the segment with negative slope are unstable, so that in the interval there are two coexisting stable stationary states: this phenomenon is called optical bistability.[11] If the input intensity [math]\displaystyle{ |E_\text{in}|^2 }[/math] is increased and then decreased, one covers a hysteresis cycle.

If we refer to the modes of the empty cavity, in the case of the uniform stationary solutions described by Eq.(3) the electric field is singlemode, corresponding to the mode of frequency [math]\displaystyle{ \omega_c }[/math] quasi-resonant with the input frequency [math]\displaystyle{ \omega_0 }[/math].

In the transverse configuration of Eq.(1), in the case of these stationary solutions E corresponds to a singlemode plane wave [math]\displaystyle{ e^{i(k_x x+k_y y)} }[/math] with [math]\displaystyle{ k_x=k_y=0 }[/math], where [math]\displaystyle{ k_x }[/math] and [math]\displaystyle{ k_y }[/math] are the transverse components of the wave vector, exactly as the input field [math]\displaystyle{ E_\text{in} }[/math].

The cubic Kerr nonlinearity of Eqs.(1) and (2) gives rise to four-wave mixing (FWM), which can generate other modes, so that the envelope [math]\displaystyle{ E }[/math] displays a spatial pattern: in the transverse plane in the case of Eq.(1), along the cavity in the case of Eq.(2).

Transverse patterns and cavity solitons

In the transverse case of Eq.(1) the pattern arises from the interplay of FWM and diffraction. The FWM can give rise, for example, to processes in which pairs of photons with [math]\displaystyle{ k_x=k_y=0 }[/math] are absorbed and, simultaneously, the system emits pairs of photons with [math]\displaystyle{ k_x=\bar{k}_x }[/math], [math]\displaystyle{ k_y=0 }[/math] and [math]\displaystyle{ k_x=-\bar{k}_x }[/math], [math]\displaystyle{ k_y=0 }[/math] in such a way that the total energy of photons, and their total momentum, are conserved (Fig.4).

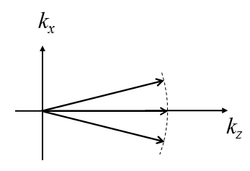
Figure 4. A four-wave mixing process in which two photons with [math]\displaystyle{ k_x=k_y=0 }[/math] are absorbed and two photons with [math]\displaystyle{ k_x=\bar{k}_x, k_y=0 }[/math] and [math]\displaystyle{ k_x=-\bar{k}_x,k_y=0 }[/math] are emitted. [math]\displaystyle{ k_x }[/math], [math]\displaystyle{ k_y }[/math] and [math]\displaystyle{ k_z }[/math] are the components of the wave-vectors.

Actually further FWM processes enter into play, so that [math]\displaystyle{ E(x,y) }[/math] assumes the configuration of a hexagonal pattern [12](see Fig.5).

Figure 5. A typical pattern configuration that arises in the transverse planes in the output is a hexagonal pattern.

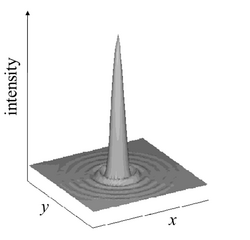
A pattern displays an ordered array of intensity peaks. It is possible to generate also isolated intensity peaks,[13] that are called cavity solitons (see Fig. 6). Since cavity solitons can be “written”and “erased” one by one in the transverse plane like in a blackboard, they are of great interest for applications to optical information processing and telecommunications.

Figure 6. A typical Kerr cavity soliton in the transverse plane showing a bright peak in the dark background with diffraction rings.

Longitudinal patterns and cavity solitons

In the longitudinal case of Eq.(2) the patterns arise from the interplay between FWM and dispersion. The FWM can give rise, for example, to processes in which pairs of photons of the longitudinal mode quasi-resonant with [math]\displaystyle{ \omega_0 }[/math] are absorbed and, simultaneously, the system emits photon pairs corresponding to cavity modes symmetrically adjacent to the quasi-resonant mode, in such a way that the total photon energy, as well as the total longitudinal photon momentum, are conserved.

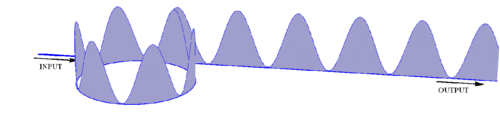
Figure 7. Example of longitudinal pattern that travels along the cavity with the velocity of light in the medium and gives rise to a periodic sequence of pulses in the output.

Figure 7 shows an example of the patterns that are generated, and travel along the cavity and out of the cavity. Like in the transverse case, also in the longitudinal configuration single or multiple Kerr cavity solitons can be generated; Figure 8 illustrates the case of a single cavity soliton that circulates in the cavity and produces a sequence of narrow pulses in the output. Such solitons have been observed for the first time in a fiber cavity.[14]

Figure 8. Longitudinal Kerr cavity solitons.

It is important to note that the instability which originates longitudinal patterns and cavity solitons in the LLE is a special case of the multimode instability of optical bistability, predicted by Bonifacio and Lugiato in [15] and first observed experimentally in.[16]

Microresonator Kerr frequency combs and cavity solitons

Optical frequency combs constitute an equidistant set of laser frequencies that can be employed to count the cycles of light. This technique, introduced by Theodor Haensch[17] and John Hall[18] using mode-locked lasers, has led to myriad applications. The work [8] demonstrated the realization of broadband optical frequency combs exploiting the whispering gallery modes activated by a CW laser field injected into a high-Q microresonator filled with a Kerr medium, that gives rise to FWM. Since that time Kerr frequency combs (KFC), whose bandwidth can exceed an octave with repetition rates in the microwave to THz frequencies, have been generated in a wide variety of microresonators; for reviews on this subject see e.g.[19][20] They offer substantial potential for miniaturization and chip-scale photonic integration, as well as for power reduction. Today KFC generation is a mature field, and this technology has been applied to several areas, including coherent telecommunications, spectroscopy, atomic clocks as well as laser ranging and astrophysical spectrometer calibration.

A key impetus to these developments has been the realization of Kerr cavity solitons in microresonators,[21] opening the possibility of utilizing Kerr cavity solitons in photonic integrated microresonators.

The longitudinal LLE (2) provides a spatio-temporal picture of the involved phenomena, but from the spectral viewpoint its solutions correspond to KFC. The link between the topic of optical KFC and the LLE was theoretically developed in.[21][22][23][24][25] These authors showed that the LLE (or generalizations including higher order dispersion terms) is the model which describes the generation of KFC and is capable of predicting their properties when the system parameters are varied. The spontaneous formation of spatial patterns and solitons travelling along the cavity described by the LLE is the spatiotemporal equivalent of the frequency combs and governs their features. The rather idealized conditions assumed in the formulation of the LLE, especially the high-Q condition, have been perfectly materialized by the spectacular technological progress that has occurred in the meantime in the field of photonics and has led, in particular, to the discovery of KFC.

The Suchkov-Letokhov equation

The averaging over longitudinal coordinate [math]\displaystyle{ z }[/math] results in the "mean-field" SLE equation where longitudinal derivative is absent:

[math]\displaystyle{ \frac{\; \omega_0\ }{ k_0 c^2} \frac{\partial E}{\partial t} - \tfrac{1}{2 k_0 }\ i\ \nabla^2_\perp E = \frac{1}{\varepsilon_0 k_0 c^2}\frac{\partial^2}{\partial t^2}\mathbf{P}^\text{NL}~ }[/math].

Rigorous procedure [26] demonstrated that this precursor of LLE is applicable to modeling of the nonstationary evolution of the transverse mode pattern in the Disk laser (1966) . Under condition of stationary Kerr nonlinearity SLE reduces to LLE.

Quantum aspects

The two photons that, as shown in Fig.4, are emitted in symmetrically tilted directions in the FWM process, are in a state of quantum entanglement: they are precisely correlated, for example in energy and momentum. This fact is fundamental for the quantum aspects of optical patterns. For instance, the difference between the intensities of the two symmetrical beams is squeezed, i.e. exhibits fluctuations below the shot noise level;[27] the longitudinal analogue of this phenomenon has been observed experimentally in KFC.[28] In turn, such quantum aspects are basic for the field of quantum imaging.[29][30]

Review articles

For reviews on the subject of the LLE, see also.[31][32][33]

See also

References

  1. ↑ Siegman, Anthony E. (1986). Lasers. University Science Books. p. 2. ISBN 978-0-935702-11-8. https://archive.org/details/lasers0000sieg. 
  2. ↑ Kryukov, P G; Letokhov, V S (1970). "Propagation of a Light pulse in a Resonantly amplifying (absorbing) medium". Sov. Phys. Usp. 12 (5): 641–672. doi:10.1070/PU1970v012n05ABEH003957. https://ufn.ru/en/articles/1970/5/c/. 
  3. ↑ Suchkov, A F (1966). "Effect of inhomogeneities on the operation regime of solid-state lasers". Sov. Phys. JETP 22 (5): 1026. Bibcode: 1966JETP...22.1026S. http://jetp.ras.ru/cgi-bin/e/index/e/22/5/p1026?a=list. 
  4. ↑ 4.0 4.1 4.2 Lugiato, L.A.; Lefever, R. (1987). "Spatial Dissipative Structures in Passive Optical Systems". Physical Review Letters 58 (21): 2209–2211. doi:10.1103/PhysRevLett.58.2209. PMID 10034681. Bibcode: 1987PhRvL..58.2209L. 
  5. ↑ Turing, A.M.. (1952). "The chemical basis of morphogenesis". Philosophical Transactions of the Royal Society of London B: Biological Sciences 237 (641): 37–72. doi:10.1098/rstb.1952.0012. Bibcode: 1952RSPTB.237...37T. 
  6. ↑ Nicolis, G.; Prigogine, I. (1977). Self-organization in nonequilibrium systems. From dissipative structures to order through fluctuations. Wiley, New York. ISBN 978-0471024019. 
  7. ↑ Haken, H. (1983). Self-organization in nonequilibrium systems. From dissipative structures to order through fluctuations. Berlin: Springer Verlag. ISBN 978-3-642-88338-5. 
  8. ↑ 8.0 8.1 "Optical frequency comb generation from a monolithic microresonator". Nature 450 (7173): 1214–1217. 2007. doi:10.1038/nature06401. PMID 18097405. Bibcode: 2007Natur.450.1214D. 
  9. ↑ Haelterman, M.; Trillo, S.; Wabnitz, S. (1992). "Dissipative modulation instability in a nonlinear dispersive ring cavity". Optics Communications 91 (5–6): 401–407. doi:10.1016/0030-4018(92)90367-Z. Bibcode: 1992OptCo..91..401H. 
  10. ↑ Brambilla, M.; Castelli, F.; Gatti, A.; Lugiato, L.A.; Prati, F. (1993). "Instabilities and quantum-noise reduction in nonlinear-optical mixing". SUSSP Proceedings 41: 115–136. 
  11. ↑ Gibbs, H.M. (1985). Optical bistability: controlling light by light. Academic Press, Inc., Orlando, Florida. ISBN 978-0122819407. 
  12. ↑ Gomila, D.; Jacobo, A.; Matias, M.A.; Colet, P. (2007). "Phase-space structure of two-dimensional excitable localized structures". Physical Review E 75 (2): 026217. doi:10.1103/PhysRevE.75.026217. PMID 17358415. Bibcode: 2007PhRvE..75b6217G. https://digital.csic.es/bitstream/10261/6146/2/PhysRevE_75_026217.pdf. 
  13. ↑ Scroggie, A.J.; Firth, W.J.; McDonald s, G.S.; Tlidi, M.; Lugiato, L.A.; Lefever, R. (1994). "Pattern formation in a passive Kerr cavity". Chaos, Solitons and Fractals 4 (8–9): 1323–1354. doi:10.1016/0960-0779(94)90084-1. Bibcode: 1994CSF.....4.1323S. 
  14. ↑ Leo, F.; Coen, S.; Kockaert, P.; Gorza, S.P.; Emplit, P.; Haelterman, M. (2010). "Temporal cavity solitons in one-dimensional Kerr media as bits in an all-optical buffer". Nature Photonics 4 (7): 471–476. doi:10.1038/nphoton.2010.120. Bibcode: 2010NaPho...4..471L. 
  15. ↑ Bonifacio, R.; Lugiato, L.A. (1978). "Instabilities for a coherently driven absorber in a ring cavity". Lettere al Nuovo Cimento 21 (15): 510–516. doi:10.1007/bf02763162. 
  16. ↑ Segard, B.; Macke, B. (1988). "Self-pulsing in intrinsic optical bistability with two-level molecules". Physical Review Letters 60 (5): 412–415. doi:10.1103/PhysRevLett.60.412. PMID 10038540. Bibcode: 1988PhRvL..60..412S. 
  17. ↑ Udem, T.; Holzwarth, R.; Hänsch t, T.W. (2002). "Optical frequency metrology". Nature 416 (6877): 233–237. doi:10.1038/416233a. PMID 11894107. Bibcode: 2002Natur.416..233U. 
  18. ↑ Jones, D.J.; Diddams, S.A.; Ranka, J.K.; Stentz, A.; Windeler, R.S.; Hall, J.L.; Curdiff, S.T. (2000). "Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis". Science 288 (5466): 635–639. doi:10.1126/science.288.5466.635. PMID 10784441. Bibcode: 2000Sci...288..635J. https://scholar.colorado.edu/cgi/viewcontent.cgi?article=1059&context=phys_facpapers. 
  19. ↑ Herr, T.; Gorodetsky, M.L.; Kippenberg, T.J. (2015). "Chap. 6 : Dissipative Kerr Solitons in Optical Microresonators". in Grelu, Philippe. Nonlinear Optical Cavity Dynamics: From Microresonators to Fiber Lasers. Wiley‐VCH Verlag GmbH. pp. 129–162. doi:10.1002/9783527686476.ch6. ISBN 9783527413324. 
  20. ↑ "Kerr optical frequency combs: theory, applications and perspectives". Nanophotonics 5 (2): 214–230. 2016. doi:10.1515/nanoph-2016-0013. Bibcode: 2016Nanop...5...13C. 
  21. ↑ 21.0 21.1 Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. (2014). "Temporal solitons in optical microresonators". Nature Photonics 8 (2): 145–152. doi:10.1038/nphoton.2013.343. Bibcode: 2014NaPho...8..145H. 
  22. ↑ Matsko, A.B.; Savchenkov, A.A.; Liang, W.; Ilchenko, V.S.; Seidel, D.; Maleki, L. (2011). "Mode-locked Kerr frequency combs". Optics Letters 36 (15): 2845–7. doi:10.1364/OL.36.002845. PMID 21808332. Bibcode: 2011OptL...36.2845M. 
  23. ↑ Herr, T.; Brasch, V.; Gorodetsky, M.L.; Kippenberg, T.J. (2012). "Soliton mode-locking in optical microresonators". arXiv:1211.0733v1 [physics.optics]. (arXiv version of Ref.18)
  24. ↑ Chembo, Y.K.; Menyuk, C.R. (2013). "Spatiotemporal Lugiato-Lefever formalism for Kerr-comb generation in whispering-gallery-mode resonators". Physical Review A 87 (5): 053852. doi:10.1103/PhysRevA.87.053852. Bibcode: 2013PhRvA..87e3852C. 
  25. ↑ Coen, S.; Randle, H.G.; Sylvestre, T. (2013). "Modeling of octave spanning Kerr frequency combs using a generalized mean-field Lugiato Lefever model". Optics Letters 38 (1): 37–39. doi:10.1364/OL.38.000037. PMID 23282830. Bibcode: 2013OptL...38...37C. 
  26. ↑ Letokhov, V S; Suchkov, A F (1966). "Generation Dynamics of a Giant Coherent Light Pulse". Sov. Phys. JETP 23 (4): 764. Bibcode: 1966JETP...23..764L. http://jetp.ras.ru/cgi-bin/e/index/e/23/4/p763?a=list. 
  27. ↑ Lugiato, L.A.; Castelli, F. (1992). "Quantum noise-reduction in a spatial dissipative structure". Physical Review Letters 68 (22): 3284–3286. doi:10.1103/PhysRevLett.68.3284. PMID 10045663. Bibcode: 1992PhRvL..68.3284L. 
  28. ↑ Dutt, A.; Luke, K.; Manipatruni, S.; Gaeta, A.L.; Nussenzveig, P.; Lipson, M. (2015). "On-chip optical squeezing". Physical Review Applied 3 (4): 044005. doi:10.1103/PhysRevApplied.3.044005. Bibcode: 2015PhRvP...3d4005D. 
  29. ↑ Gatti, A.; Brambilla, E.; Lugiato, L.A. (2008). Wolf, E.. ed. Quantum Imaging. LI. 251–348. doi:10.1016/S0079-6638(07)51005-X. ISBN 9780444532114. 
  30. ↑ Kolobov, M.I. (1999). "The spatial behavior of nonclassical light". Reviews of Modern Physics 71 (5): 1539–1589. doi:10.1103/RevModPhys.71.1539. Bibcode: 1999RvMP...71.1539K. 
  31. ↑ Lugiato, L.A.; Prati, F.; Brambilla, M. (2015). "Chapter 28: The Lugiato Lefever Model". Nonlinear Optical Systems. Cambridge University Press. doi:10.1017/CBO9781107477254.032. ISBN 9781107477254. 
  32. ↑ Castelli, F.; Brambilla, M.; Gatti, M.; Prati, F.; Lugiato, L.A. (2017). "The LLE, pattern formation and a novel coherent source". The European Physical Journal D 71 (4): 84. doi:10.1140/epjd/e2017-70754-1. Bibcode: 2017EPJD...71...84C. https://air.unimi.it/bitstream/2434/502714/2/LLE%20proofs.pdf. 
  33. ↑ Lugiato, L.A.; Prati, F.; Gorodetsky, M.L.; Kippenberg, T.J.. "From the LLE to microresonator based soliton Kerr frequency combs". Philosophical Transactions of the Royal Society of London A. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Lugiato–Lefever_equation&oldid=3003675"