Physics:Four-wave mixing
Four-wave mixing (FWM) is an intermodulation phenomenon in nonlinear optics, whereby interactions between two or three wavelengths produce two or one new wavelengths. It is similar to the third-order intercept point in electrical systems. Four-wave mixing can be compared to the intermodulation distortion in standard electrical systems. It is a parametric nonlinear process, in that the energy of the incoming photons is conserved. FWM is a phase-sensitive process, in that the efficiency of the process is strongly affected by phase matching conditions.
Mechanism
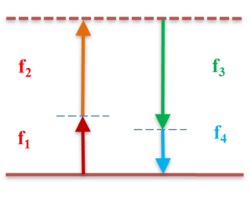
When three frequencies (f1, f2, and f3) interact in a nonlinear medium, they give rise to a fourth frequency (f4) which is formed by the scattering of the incident photons, producing the fourth photon.
Given inputs f1, f2, and f3, the nonlinear system will produce
From calculations with the three input signals, it is found that 12 interfering frequencies are produced, three of which lie on one of the original incoming frequencies. Note that these three frequencies which lie at the original incoming frequencies are typically attributed to self-phase modulation and cross-phase modulation, and are naturally phase-matched unlike FWM.
Sum- and difference-frequency generation
Two common forms of four-wave mixing are dubbed sum-frequency generation and difference-frequency generation. In sum-frequency generation three fields are input and the output is a new high frequency field at the sum of the three input frequencies. In difference-frequency generation, the typical output is the sum of two minus the third.
A condition for efficient generation of FWM is phase matching: the associated k-vectors of the four components must add to zero when they are plane waves. This becomes significant since sum- and difference-frequency generation are often enhanced when resonance in the mixing media is exploited. In many configurations the sum of the first two photons will be tuned close to a resonant state.[1] However, close to resonances the index of refraction changes rapidly and makes addition four co-linear k-vectors fail to add exactly to zero—thus long mixing path lengths are not always possible as the four component lose phase lock. Consequently, beams are often focused both for intensity but also to shorten the mixing zone.
In gaseous media an often overlooked complication is that light beams are rarely plane waves but are often focused for extra intensity, this can add an addition pi-phase shift to each k-vector in the phase matching condition.[2][3] It is often very hard to satisfy this in the sum-frequency configuration but it is more easily satisfied in the difference-frequency configuration (where the pi phase shifts cancel out).[1] As a result, difference-frequency is usually more broadly tunable and easier to set up than sum-frequency generation, making it preferable as a light source even though it's less quantum efficient than sum-frequency generation.
The special case of sum-frequency generation where all the input photons have the same frequency (and wavelength) is Third-Harmonic Generation (THG).
Degenerate four-wave mixing
Four-wave mixing is also present if only two components interact. In this case the term
couples three components, thus generating so-called degenerate four-wave mixing, showing identical properties to the case of three interacting waves.[4]
Adverse effects of FWM in fiber-optic communications
FWM is a fiber-optic characteristic that affects wavelength-division multiplexing (WDM) systems, where multiple optical wavelengths are spaced at equal intervals or channel spacing. The effects of FWM are pronounced with decreased channel spacing of wavelengths (such as in dense WDM systems) and at high signal power levels. High chromatic dispersion decreases FWM effects, as the signals lose coherence, or in other words, the phase mismatch between the signals increases. The interference FWM caused in WDM systems is known as interchannel crosstalk. FWM can be mitigated by using uneven channel spacing or fiber that increases dispersion. For the special case where the three frequencies are close to degenerate, then optical separation of the difference frequency can be technically challenging.
Applications
FWM finds applications in optical phase conjugation, parametric amplification, supercontinuum generation, Vacuum Ultraviolet light generation, modulation transfer spectroscopy[5], and in microresonator based frequency comb generation. Parametric amplifiers and oscillators based on four-wave mixing use the third order nonlinearity, as opposed to most typical parametric oscillators which use the second-order nonlinearity. Apart from these classical applications, four-wave mixing has shown promise in the quantum optical regime for generating single photons,[6] correlated photon pairs,[7][8] squeezed light[9][10] and entangled photons.[11]
See also
- Kerr frequency comb
- Lugiato–Lefever equation
- Optical Kerr effect
- Optical phase conjugation, phase conjugate mirror
- Supercontinuum generation
References
- ↑ 1.0 1.1 Strauss, CEM; Funk, DJ (1991). "Broadly tunable difference-frequency generation of VUV using two-photon resonances in H2 and Kr". Optics Letters 16 (15): 1192–4. doi:10.1364/ol.16.001192. PMID 19776917. Bibcode: 1991OptL...16.1192S. https://www.osapublishing.org/ol/fulltext.cfm?uri=ol-16-15-1192&id=10705.
- ↑ Cardoso, GC; Tabosa, JWR (2000). "Four-wave mixing in dressed cold cesium atoms". Optics Communications 185 (4–6): 353. doi:10.1016/S0030-4018(00)01033-6. Bibcode: 2000OptCo.185..353C.
- ↑ Cardoso, GC; Tabosa, JWR (2002). "Saturated lineshapes and high-order susceptibilities of cold cesium atoms observed via a transferred population grating". Optics Communications 210 (3–6): 271. doi:10.1016/S0030-4018(02)01820-5. Bibcode: 2002OptCo.210..271C.
- ↑ Cvijetic, Djordjevic, Milorad, Ivan B. (2013). Advanced Optical Communication Systems and Networks. Artech House. pp. 314 to 217. ISBN 978-1-60807-555-3.
- ↑ McCarron, D J; King, S A; Cornish, S L (2008-10-01). "Modulation transfer spectroscopy in atomic rubidium". Measurement Science and Technology 19 (10). doi:10.1088/0957-0233/19/10/105601. ISSN 0957-0233. https://iopscience.iop.org/article/10.1088/0957-0233/19/10/105601.
- ↑ Fan, Bixuan; Duan, Zhenglu; Zhou, Lu; Yuan, Chunhua; Ou, Z. Y.; Zhang, Weiping (2009-12-03). "Generation of a single-photon source via a four-wave mixing process in a cavity". Physical Review A 80 (6). doi:10.1103/PhysRevA.80.063809. Bibcode: 2009PhRvA..80f3809F.
- ↑ Sharping, Jay E.; Fiorentino, Marco; Coker, Ayodeji; Kumar, Prem; Windeler, Robert S. (2001-07-15). "Four-wave mixing in microstructure fiber" (in EN). Optics Letters 26 (14): 1048–1050. doi:10.1364/OL.26.001048. ISSN 1539-4794. PMID 18049515. Bibcode: 2001OptL...26.1048S.
- ↑ Wang, L. J.; Hong, C. K.; Friberg, S. R. (2001). "Generation of correlated photons via four-wave mixing in optical fibres" (in en). Journal of Optics B: Quantum and Semiclassical Optics 3 (5): 346. doi:10.1088/1464-4266/3/5/311. ISSN 1464-4266. Bibcode: 2001JOptB...3..346W. http://stacks.iop.org/1464-4266/3/i=5/a=311.
- ↑ Slusher, R. E.; Yurke, B.; Grangier, P.; LaPorta, A.; Walls, D. F.; Reid, M. (1987-10-01). "Squeezed-light generation by four-wave mixing near an atomic resonance" (in EN). JOSA B 4 (10): 1453–1464. doi:10.1364/JOSAB.4.001453. ISSN 1520-8540. Bibcode: 1987JOSAB...4.1453S.
- ↑ Dutt, Avik; Luke, Kevin; Manipatruni, Sasikanth; Gaeta, Alexander L.; Nussenzveig, Paulo; Lipson, Michal (2015-04-13). "On-Chip Optical Squeezing". Physical Review Applied 3 (4). doi:10.1103/PhysRevApplied.3.044005. Bibcode: 2015PhRvP...3d4005D.
- ↑ Takesue, Hiroki; Inoue, Kyo (2004-09-30). "Generation of polarization-entangled photon pairs and violation of Bell's inequality using spontaneous four-wave mixing in a fiber loop". Physical Review A 70 (3). doi:10.1103/PhysRevA.70.031802. Bibcode: 2004PhRvA..70c1802T.
External links
 |
