Matched Z-transform method

From HandWiki
The s-plane poles and zeros of a 5th-order Chebyshev type II lowpass filter to be approximated as a discrete-time filter
The z-plane poles and zeros of the discrete-time Chebyshev filter, as mapped into the z-plane using the matched Z-transform method with T = 1/10 second. The labeled frequency points and band-edge dotted lines have also been mapped through the function z=eiωT, to show how frequencies along the iω axis in the s-plane map onto the unit circle in the z-plane.

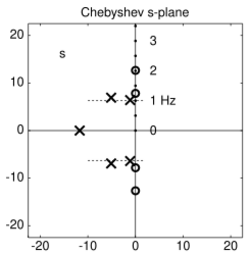
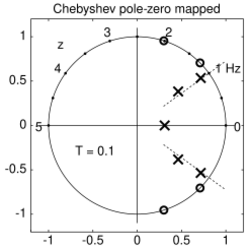
The matched Z-transform method, also called the pole–zero mapping[1][2] or pole–zero matching method,[3] and abbreviated MPZ or MZT,[4] is a technique for converting a continuous-time filter design to a discrete-time filter (digital filter) design.

The method works by mapping all poles and zeros of the s-plane design to z-plane locations [math]\displaystyle{ z=e^{sT} }[/math], for a sample interval [math]\displaystyle{ T=1 / f_\mathrm{s} }[/math].[5] So an analog filter with transfer function:

[math]\displaystyle{ H(s) = k_{\mathrm a} \frac{\prod_{i=1}^M (s-\xi_i) }{\prod_{i=1}^N (s-p_i) } }[/math]

is transformed into the digital transfer function

[math]\displaystyle{ H(z) = k_{\mathrm d} \frac{ \prod_{i=1}^M (1 - e^{\xi_iT}z^{-1})}{ \prod_{i=1}^N (1 - e^{p_iT}z^{-1})} }[/math]

The gain [math]\displaystyle{ k_{\mathrm d} }[/math] must be adjusted to normalize the desired gain, typically set to match the analog filter's gain at DC by setting [math]\displaystyle{ s=0 }[/math] and [math]\displaystyle{ z=1 }[/math] and solving for [math]\displaystyle{ k_{\mathrm d} }[/math].[3][6]

Since the mapping wraps the s-plane's [math]\displaystyle{ j\omega }[/math] axis around the z-plane's unit circle repeatedly, any zeros (or poles) greater than the Nyquist frequency will be mapped to an aliased location.[7]

In the (common) case that the analog transfer function has more poles than zeros, the zeros at [math]\displaystyle{ s=\infty }[/math] may optionally be shifted down to the Nyquist frequency by putting them at [math]\displaystyle{ z=-1 }[/math], causing the transfer function to drop off as [math]\displaystyle{ z \rightarrow -1 }[/math] in much the same manner as with the bilinear transform (BLT).[1][3][6][7]

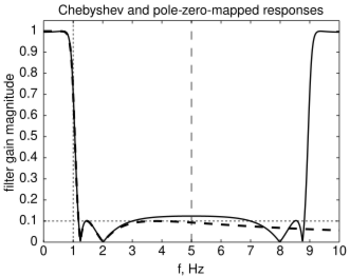
While this transform preserves stability and minimum phase, it preserves neither time- nor frequency-domain response and so is not widely used.[8][7] More common methods include the BLT and impulse invariance methods.[4] MZT does provide less high frequency response error than the BLT, however, making it easier to correct by adding additional zeros, which is called the MZTi (for "improved").[9]

A specific application of the matched Z-transform method in the digital control field is with the Ackermann's formula, which changes the poles of the controllable system; in general from an unstable (or nearby) location to a stable location.

Responses of the filter (dashed), and its discrete-time approximation (solid), for nominal cutoff frequency of 1 Hz, sample rate 1/T = 10 Hz. The discrete-time filter does not reproduce the Chebyshev equiripple property in the stopband due to the interference from cyclic copies of the response.

References

  1. ↑ 1.0 1.1 Won Young Yang (2009). Signals and Systems with MATLAB. Springer. p. 292. ISBN 978-3-540-92953-6. https://books.google.com/books?id=GnfpELDfzmEC&pg=PA292. 
  2. ↑ Bong Wie (1998). Space vehicle dynamics and control. AIAA. p. 151. ISBN 978-1-56347-261-9. https://books.google.com/books?id=n97tEQvNyVgC&pg=PA151. 
  3. ↑ 3.0 3.1 3.2 Arthur G. O. Mutambara (1999). Design and analysis of control systems. CRC Press. p. 652. ISBN 978-0-8493-1898-6. https://books.google.com/books?id=VSlHxALK6OoC&pg=PA652. 
  4. ↑ 4.0 4.1 Al-Alaoui, M. A. (February 2007). "Novel Approach to Analog-to-Digital Transforms". IEEE Transactions on Circuits and Systems I: Regular Papers 54 (2): 338–350. doi:10.1109/tcsi.2006.885982. ISSN 1549-8328. 
  5. ↑ S. V. Narasimhan and S. Veena (2005). Signal processing: principles and implementation. Alpha Science Int'l Ltd.. p. 260. ISBN 978-1-84265-199-5. https://books.google.com/books?id=8UbV8vq8uV0C&pg=PA260. 
  6. ↑ 6.0 6.1 Franklin, Gene F. (2015). Feedback control of dynamic systems. Powell, J. David, Emami-Naeini, Abbas (Seventh ed.). Boston: Pearson. pp. 607–611. ISBN 978-0133496598. OCLC 869825370. "Because physical systems often have more poles than zeros, it is useful to arbitrarily add zeros at z = -1." 
  7. ↑ 7.0 7.1 7.2 Rabiner, Lawrence R; Gold, Bernard (1975) (in en). Theory and application of digital signal processing. Englewood Cliffs, New Jersey: Prentice-Hall. pp. 224–226. ISBN 0139141014. https://archive.org/details/theoryapplicatio00rabi/page/224. "The expediency of artificially adding zeros at z = —1 to the digital system has been suggested ... but this ad hoc technique is at best only a stopgap measure. ... In general, use of impulse invariant or bilinear transformation is to be preferred over the matched z transformation." 
  8. ↑ Jackson, Leland B. (1996) (in en). Digital Filters and Signal Processing. Springer Science & Business Media. pp. 262. ISBN 9780792395591. https://books.google.com/books?id=VZ8uabI1pNMC&pg=PA262. "although perfectly usable filters can be designed in this way, no special time- or frequency-domain properties are preserved by this transformation, and it is not widely used." 
  9. ↑ Ojas, Chauhan; David, Gunness (2007-09-01). "Optimizing the Magnitude Response of Matched Z-Transform Filters ("MZTi") for Loudspeaker Equalization" (in en). Audio Engineering Society. http://www.aes.org/e-lib/browse.cfm?elib=14198.  Alt URL



Retrieved from "https://handwiki.org/wiki/index.php?title=Matched_Z-transform_method&oldid=58010"