Discrete cosine transform
A discrete cosine transform (DCT) expresses a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequencies. The DCT, first proposed by Nasir Ahmed in 1972, is a widely used transformation technique in signal processing and data compression. It is used in most digital media, including digital images (such as JPEG and HEIF), digital video (such as MPEG and H.26x), digital audio (such as Dolby Digital, MP3 and AAC), digital television (such as SDTV, HDTV and VOD), digital radio (such as AAC+ and DAB+), and speech coding (such as AAC-LD, Siren and Opus). DCTs are also important to numerous other applications in science and engineering, such as digital signal processing, telecommunication devices, reducing network bandwidth usage, and spectral methods for the numerical solution of partial differential equations.
A DCT is a Fourier-related transform similar to the discrete Fourier transform (DFT), but using only real numbers. The DCTs are generally related to Fourier series coefficients of a periodically and symmetrically extended sequence whereas DFTs are related to Fourier series coefficients of only periodically extended sequences. DCTs are equivalent to DFTs of roughly twice the length, operating on real data with even symmetry (since the Fourier transform of a real and even function is real and even), whereas in some variants the input or output data are shifted by half a sample.
There are eight standard DCT variants, of which four are common. The most common variant of discrete cosine transform is the type-II DCT, which is often called simply the DCT. This was the original DCT as first proposed by Ahmed. Its inverse, the type-III DCT, is correspondingly often called simply the inverse DCT or the IDCT. Two related transforms are the discrete sine transform (DST), which is equivalent to a DFT of real and odd functions, and the modified discrete cosine transform (MDCT), which is based on a DCT of overlapping data. Multidimensional DCTs (MD DCTs) are developed to extend the concept of DCT to multidimensional signals. A variety of fast algorithms have been developed to reduce the computational complexity of implementing DCT. One of these is the integer DCT (IntDCT),[1] an integer approximation of the standard DCT,[2]: ix, xiii, 1, 141–304 used in several ISO/IEC and ITU-T international standards.[1][2]
DCT compression, also known as block compression, compresses data in sets of discrete DCT blocks.[3] DCT blocks sizes including 8x8 pixels for the standard DCT, and varied integer DCT sizes between 4x4 and 32x32 pixels.[1][4] The DCT has a strong energy compaction property,[5][6] capable of achieving high quality at high data compression ratios.[7][8] However, blocky compression artifacts can appear when heavy DCT compression is applied.
History
The DCT was first conceived by Nasir Ahmed while working at Kansas State University. The concept was proposed to the National Science Foundation in 1972. The DCT was originally intended for image compression.[9][1] Ahmed developed a practical DCT algorithm with his PhD students T. Raj Natarajan and K. R. Rao at the University of Texas at Arlington in 1973.[9] They presented their results in a January 1974 paper, titled Discrete Cosine Transform.[5][6][10] It described what is now called the type-II DCT (DCT-II),[2]: 51 as well as the type-III inverse DCT (IDCT).[5]
Since its introduction in 1974, there has been significant research on the DCT.[10] In 1977, Wen-Hsiung Chen published a paper with C. Harrison Smith and Stanley C. Fralick presenting a fast DCT algorithm.[11][10] Further developments include a 1978 paper by M. J. Narasimha and A. M. Peterson, and a 1984 paper by B. G. Lee.[10] These research papers, along with the original 1974 Ahmed paper and the 1977 Chen paper, were cited by the Joint Photographic Experts Group as the basis for JPEG's lossy image compression algorithm in 1992.[10][12]
The discrete sine transform (DST) was derived from the DCT, by replacing the Neumann condition at x=0 with a Dirichlet condition.[2]: 35-36 The DST was described in the 1974 DCT paper by Ahmed, Natarajan and Rao.[5] A type-I DST (DST-I) was later described by Anil K. Jain in 1976, and a type-II DST (DST-II) was then described by H.B. Kekra and J.K. Solanka in 1978.[13]
In 1975, John A. Roese and Guner S. Robinson adapted the DCT for inter-frame motion-compensated video coding. They experimented with the DCT and the fast Fourier transform (FFT), developing inter-frame hybrid coders for both, and found that the DCT is the most efficient due to its reduced complexity, capable of compressing image data down to 0.25-bit per pixel for a videotelephone scene with image quality comparable to an intra-frame coder requiring 2-bit per pixel.[14][15] In 1979, Anil K. Jain and Jaswant R. Jain further developed motion-compensated DCT video compression,[16][17] also called block motion compensation.[17] This led to Chen developing a practical video compression algorithm, called motion-compensated DCT or adaptive scene coding, in 1981.[17] Motion-compensated DCT later became the standard coding technique for video compression from the late 1980s onwards.[18][19]
A DCT variant, the modified discrete cosine transform (MDCT), was developed by John P. Princen, A.W. Johnson and Alan B. Bradley at the University of Surrey in 1987,[20] following earlier work by Princen and Bradley in 1986.[21] The MDCT is used in most modern audio compression formats, such as Dolby Digital (AC-3),[22][23] MP3 (which uses a hybrid DCT-FFT algorithm),[24] Advanced Audio Coding (AAC),[25] and Vorbis (Ogg).[26]
Nasir Ahmed also developed a lossless DCT algorithm with Giridhar Mandyam and Neeraj Magotra at the University of New Mexico in 1995. This allows the DCT technique to be used for lossless compression of images. It is a modification of the original DCT algorithm, and incorporates elements of inverse DCT and delta modulation. It is a more effective lossless compression algorithm than entropy coding.[27] Lossless DCT is also known as LDCT.[28]
Applications
The DCT is the most widely used transformation technique in signal processing,[29] and by far the most widely used linear transform in data compression.[30] Uncompressed digital media as well as lossless compression have high memory and bandwidth requirements, which is significantly reduced by the DCT lossy compression technique,[7][8] capable of achieving data compression ratios from 8:1 to 14:1 for near-studio-quality,[7] up to 100:1 for acceptable-quality content.[8] DCT compression standards are used in digital media technologies, such as digital images, digital photos,[31][32] digital video,[18][33] streaming media,[34] digital television, streaming television, video on demand (VOD),[8] digital cinema,[22] high-definition video (HD video), and high-definition television (HDTV).[7][35]
The DCT, and in particular the DCT-II, is often used in signal and image processing, especially for lossy compression, because it has a strong energy compaction property.[5][6] In typical applications, most of the signal information tends to be concentrated in a few low-frequency components of the DCT. For strongly correlated Markov processes, the DCT can approach the compaction efficiency of the Karhunen-Loève transform (which is optimal in the decorrelation sense). As explained below, this stems from the boundary conditions implicit in the cosine functions.
DCTs are widely employed in solving partial differential equations by spectral methods, where the different variants of the DCT correspond to slightly different even and odd boundary conditions at the two ends of the array.
DCTs are closely related to Chebyshev polynomials, and fast DCT algorithms (below) are used in Chebyshev approximation of arbitrary functions by series of Chebyshev polynomials, for example in Clenshaw–Curtis quadrature.
General applications
The DCT is widely used in many applications, which include the following.
- Audio signal processing — audio coding, audio data compression (lossy and lossless),[36] surround sound,[22] acoustic echo and feedback cancellation, phoneme recognition, time-domain aliasing cancellation (TDAC)[37]
- Digital audio[1]
- Digital radio — Digital Audio Broadcasting (DAB+),[38] HD Radio[39]
- Speech processing — speech coding[40][41] speech recognition, voice activity detection (VAD)[37]
- Digital telephony — voice over IP (VoIP),[40] mobile telephony, video telephony,[41] teleconferencing, videoconferencing[1]
- Biometrics — fingerprint orientation, facial recognition systems, biometric watermarking, fingerprint-based biometric watermarking, palm print identification/recognition[37]
- Computers and the Internet — the World Wide Web, social media,[31][32] Internet video[42]
- Network bandwidth usage reduction[1]
- Consumer electronics[37] — multimedia systems,[1] multimedia telecommunication devices,[1] consumer devices[42]
- Cryptography — encryption, steganography, copyright protection[37]
- Data compression — transform coding, lossy compression, lossless compression[36]
- Encoding operations — quantization, perceptual weighting, entropy encoding, variable bitrate encoding[1]
- Digital media[34] — digital distribution[43]
- Streaming media[34] — streaming audio, streaming video, streaming television, video-on-demand (VOD)[8]
- Forgery detection[37]
- Geophysical transient electromagnetics (transient EM)[37]
- Images — artist identification,[37] focus and blurriness measure,[37] feature extraction[37]
- Color formatting — formatting luminance and color differences, color formats (such as YUV444 and YUV411), decoding operations such as the inverse operation between display color formats (YIQ, YUV, RGB)[1]
- Digital imaging — digital images, digital cameras, digital photography,[31][32] high-dynamic-range imaging (HDR imaging)[44]
- Image compression[37][45] — image file formats,[46] multiview image compression, progressive image transmission[37]
- Image processing — digital image processing,[1] image analysis, content-based image retrieval, corner detection, directional block-wise image representation, edge detection, image enhancement, image fusion, image segmentation, interpolation, image noise level estimation, mirroring, rotation, just-noticeable distortion (JND) profile, spatiotemporal masking effects, foveated imaging[37]
- Image quality assessment — DCT-based quality degradation metric (DCT QM)[37]
- Image reconstruction — directional textures auto inspection, image restoration, inpainting, visual recovery[37]
- Medical technology
- Electrocardiography (ECG) — vectorcardiography (VCG)[37]
- Medical imaging — medical image compression, image fusion, watermarking, brain tumor compression classification[37]
- Pattern recognition[37]
- Region of interest (ROI) extraction[37]
- Signal processing — digital signal processing, digital signal processors (DSP), DSP software, multiplexing, signaling, control signals, analog-to-digital conversion (ADC),[1] compressive sampling, DCT pyramid error concealment, downsampling, upsampling, signal-to-noise ratio (SNR) estimation, transmux, Wiener filter[37]
- Surveillance[37]
- Vehicular event data recorder camera[37]
- Video
- Digital cinema[45] — digital cinematography, digital movie cameras, video editing, film editing,[47][48] Dolby Digital audio[1][22]
- Digital television (DTV)[7] — digital television broadcasting,[45] standard-definition television (SDTV), high-definition TV (HDTV),[7][35] HDTV encoder/decoder chips, ultra HDTV (UHDTV)[1]
- Digital video[18][33] — digital versatile disc (DVD),[45] high-definition (HD) video[7][35]
- Video coding — video compression,[1] video coding standards,[37] motion estimation, motion compensation, inter-frame prediction, motion vectors,[1] 3D video coding, local distortion detection probability (LDDP) model, moving object detection, Multiview Video Coding (MVC)[37]
- Video processing — motion analysis, 3D-DCT motion analysis, video content analysis, data extraction,[37] video browsing,[49] professional video production[50]
- Watermarking — digital watermarking, image watermarking, video watermarking, 3D video watermarking, reversible data hiding, watermarking detection[37]
- Wireless technology
- Wireless sensor network (WSN) — wireless acoustic sensor networks[37]
Visual media standards
The DCT-II is an important image compression technique. It is used in image compression standards such as JPEG, and video compression standards such as H.26x, MJPEG, MPEG, DV, Theora and Daala. There, the two-dimensional DCT-II of blocks are computed and the results are quantized and entropy coded. In this case, is typically 8 and the DCT-II formula is applied to each row and column of the block. The result is an 8 × 8 transform coefficient array in which the element (top-left) is the DC (zero-frequency) component and entries with increasing vertical and horizontal index values represent higher vertical and horizontal spatial frequencies.
The integer DCT, an integer approximation of the DCT,[2][1] is used in Advanced Video Coding (AVC),[52][1] introduced in 2003, and High Efficiency Video Coding (HEVC),[4][1] introduced in 2013. The integer DCT is also used in the High Efficiency Image Format (HEIF), which uses a subset of the HEVC video coding format for coding still images.[4] AVC uses 4 x 4 and 8 x 8 blocks. HEVC and HEIF use varied block sizes between 4 x 4 and 32 x 32 pixels.[4][1] As of 2019[update], AVC is by far the most commonly used format for the recording, compression and distribution of video content, used by 91% of video developers, followed by HEVC which is used by 43% of developers.[43]
Image formats
| Image compression standard | Year | Common applications |
|---|---|---|
| JPEG[1] | 1992 | The most widely used image compression standard[53][54] and digital image format.[46] |
| JPEG XR | 2009 | Open XML Paper Specification |
| WebP | 2010 | A graphic format that supports the lossy compression of digital images. Developed by Google. |
| High Efficiency Image Format (HEIF) | 2013 | Image file format based on HEVC compression. It improves compression over JPEG,[4] and supports animation with much more efficient compression than the animated GIF format.[55] |
| BPG | 2014 | Based on HEVC compression |
| JPEG XL[56] | 2020 | A royalty-free raster-graphics file format that supports both lossy and lossless compression. |
Video formats
| Video coding standard | Year | Common applications |
|---|---|---|
| H.261[57][58] | 1988 | First of a family of video coding standards. Used primarily in older video conferencing and video telephone products. |
| Motion JPEG (MJPEG)[59] | 1992 | QuickTime, video editing, non-linear editing, digital cameras |
| MPEG-2 Video (H.262)[60] | 1995 | Storage and handling of digital images in broadcast applications, digital television, HDTV, cable, satellite, high-speed Internet, DVD video distribution |
| DV | 1995 | Camcorders, digital cassettes |
| H.263 (MPEG-4 Part 2)[57] | 1996 | Video telephony over public switched telephone network (PSTN), H.320, Integrated Services Digital Network (ISDN)[61][62] |
| Advanced Video Coding (AVC, H.264, MPEG-4)[1][52] | 2003 | Popular HD video recording, compression and distribution format, Internet video, YouTube, Blu-ray Discs, HDTV broadcasts, web browsers, streaming television, mobile devices, consumer devices, Netflix,[42] video telephony, FaceTime[41] |
| Theora | 2004 | Internet video, web browsers |
| VC-1 | 2006 | Windows media, Blu-ray Discs |
| Apple ProRes | 2007 | Professional video production.[50] |
| VP9 | 2010 | A video codec developed by Google used in the WebM container format with HTML5. |
| High Efficiency Video Coding (HEVC, H.265)[1][4] | 2013 | Successor to the H.264 standard, having substantially improved compression capability |
| Daala | 2013 | Research video format by Xiph.org |
| AV1[63] | 2018 | An open source format based on VP10 (VP9's internal successor), Daala and Thor; used by content providers such as YouTube[64][65] and Netflix.[66][67] |
MDCT audio standards
General audio
Speech coding
| Speech coding standard | Year | Common applications |
|---|---|---|
| AAC-LD (LD-MDCT)[77] | 1999 | Mobile telephony, voice-over-IP (VoIP), iOS, FaceTime[41] |
| Siren[40] | 1999 | VoIP, wideband audio, G.722.1 |
| G.722.1[78] | 1999 | VoIP, wideband audio, G.722 |
| G.729.1[79] | 2006 | G.729, VoIP, wideband audio,[79] mobile telephony |
| EVRC-WB[38]: 31, 478] | 2007 | Wideband audio |
| G.718[80] | 2008 | VoIP, wideband audio, mobile telephony |
| G.719[38] | 2008 | Teleconferencing, videoconferencing, voice mail |
| CELT[81] | 2011 | VoIP,[82][83] mobile telephony |
| Enhanced Voice Services (EVS)[84] | 2014 | Mobile telephony, VoIP, wideband audio |
Multidimensional DCT
Multidimensional DCTs (MD DCTs) have several applications, mainly 3-D DCTs such as the 3-D DCT-II, which has several new applications like Hyperspectral Imaging coding systems,[85] variable temporal length 3-D DCT coding,[86] video coding algorithms,[87] adaptive video coding[88] and 3-D Compression.[89] Due to enhancement in the hardware, software and introduction of several fast algorithms, the necessity of using MD DCTs is rapidly increasing. DCT-IV has gained popularity for its applications in fast implementation of real-valued polyphase filtering banks,[90] lapped orthogonal transform[91][92] and cosine-modulated wavelet bases.[93]
Digital signal processing
DCT plays an important role in digital signal processing specifically data compression. The DCT is widely implemented in digital signal processors (DSP), as well as digital signal processing software. Many companies have developed DSPs based on DCT technology. DCTs are widely used for applications such as encoding, decoding, video, audio, multiplexing, control signals, signaling, and analog-to-digital conversion. DCTs are also commonly used for high-definition television (HDTV) encoder/decoder chips.[1]
Compression artifacts
A common issue with DCT compression in digital media are blocky compression artifacts,[94] caused by DCT blocks.[3] In a DCT algorithm, an image (or frame in an image sequence) is divided into square blocks which are processed independently from each other, then the DCT blocks is taken within each block and the resulting DCT coefficients are quantized. This process can cause blocking artifacts, primarily at high data compression ratios.[94] This can also cause the mosquito noise effect, commonly found in digital video.[95]
DCT blocks are often used in glitch art.[3] The artist Rosa Menkman makes use of DCT-based compression artifacts in her glitch art,[96] particularly the DCT blocks found in most digital media formats such as JPEG digital images and MP3 audio.[3] Another example is Jpegs by German photographer Thomas Ruff, which uses intentional JPEG artifacts as the basis of the picture's style.[97][98]
Informal overview
Like any Fourier-related transform, DCTs express a function or a signal in terms of a sum of sinusoids with different frequencies and amplitudes. Like the DFT, a DCT operates on a function at a finite number of discrete data points. The obvious distinction between a DCT and a DFT is that the former uses only cosine functions, while the latter uses both cosines and sines (in the form of complex exponentials). However, this visible difference is merely a consequence of a deeper distinction: a DCT implies different boundary conditions from the DFT or other related transforms.
The Fourier-related transforms that operate on a function over a finite domain, such as the DFT or DCT or a Fourier series, can be thought of as implicitly defining an extension of that function outside the domain. That is, once you write a function as a sum of sinusoids, you can evaluate that sum at any , even for where the original was not specified. The DFT, like the Fourier series, implies a periodic extension of the original function. A DCT, like a cosine transform, implies an even extension of the original function.

However, because DCTs operate on finite, discrete sequences, two issues arise that do not apply for the continuous cosine transform. First, one has to specify whether the function is even or odd at both the left and right boundaries of the domain (i.e. the min-n and max-n boundaries in the definitions below, respectively). Second, one has to specify around what point the function is even or odd. In particular, consider a sequence abcd of four equally spaced data points, and say that we specify an even left boundary. There are two sensible possibilities: either the data are even about the sample a, in which case the even extension is dcbabcd, or the data are even about the point halfway between a and the previous point, in which case the even extension is dcbaabcd (a is repeated).
Each boundary can be either even or odd (2 choices per boundary) and can be symmetric about a data point or the point halfway between two data points (2 choices per boundary), for a total of 2 × 2 × 2 × 2 = 16 possibilities. These choices lead to all the standard variations of DCTs and also discrete sine transforms (DSTs). Half of these possibilities, those where the left boundary is even, correspond to the 8 types of DCT; the other half are the 8 types of DST.
These different boundary conditions strongly affect the applications of the transform and lead to uniquely useful properties for the various DCT types. Most directly, when using Fourier-related transforms to solve partial differential equations by spectral methods, the boundary conditions are directly specified as a part of the problem being solved. Or, for the MDCT (based on the type-IV DCT), the boundary conditions are intimately involved in the MDCT's critical property of time-domain aliasing cancellation. In a more subtle fashion, the boundary conditions are responsible for the energy compactification properties that make DCTs useful for image and audio compression, because the boundaries affect the rate of convergence of any Fourier-like series.
In particular, it is well known that any discontinuities in a function reduce the rate of convergence of the Fourier series so that more sinusoids are needed to represent the function with a given accuracy. The same principle governs the usefulness of the DFT and other transforms for signal compression; the smoother a function is, the fewer terms in its DFT or DCT are required to represent it accurately, and the more it can be compressed.[lower-alpha 1] However, the implicit periodicity of the DFT means that discontinuities usually occur at the boundaries: any random segment of a signal is unlikely to have the same value at both the left and right boundaries.[lower-alpha 2] In contrast, a DCT where both boundaries are even always yields a continuous extension at the boundaries (although the slope is generally discontinuous). This is why DCTs, and in particular DCTs of types I, II, V, and VI (the types that have two even boundaries) generally perform better for signal compression than DFTs and DSTs. In practice, a type-II DCT is usually preferred for such applications, in part for reasons of computational convenience.
Formal definition
Formally, the discrete cosine transform is a linear, invertible function (where denotes the set of real numbers), or equivalently an invertible N × N square matrix. There are several variants of the DCT with slightly modified definitions. The N real numbers are transformed into the N real numbers according to one of the formulas:
DCT-I
Some authors further multiply the and terms by and correspondingly multiply the and terms by which, if one further multiplies by an overall scale factor of , makes the DCT-I matrix orthogonal but breaks the direct correspondence with a real-even DFT.
The DCT-I is exactly equivalent (up to an overall scale factor of 2), to a DFT of real numbers with even symmetry. For example, a DCT-I of real numbers is exactly equivalent to a DFT of eight real numbers (even symmetry), divided by two. (In contrast, DCT types II-IV involve a half-sample shift in the equivalent DFT.)
Note, however, that the DCT-I is not defined for less than 2, while all other DCT types are defined for any positive .
Thus, the DCT-I corresponds to the boundary conditions: is even around and even around ; similarly for .
DCT-II
The DCT-II is probably the most commonly used form, and is often simply referred to as the DCT.[5][6]
This transform is exactly equivalent (up to an overall scale factor of 2) to a DFT of real inputs of even symmetry, where the even-indexed elements are zero. That is, it is half of the DFT of the inputs where , for , , and for . DCT-II transformation is also possible using signal followed by a multiplication by half shift. This is demonstrated by Makhoul.[citation needed]
Some authors further multiply the term by and multiply the rest of the matrix by an overall scale factor of (see below for the corresponding change in DCT-III). This makes the DCT-II matrix orthogonal, but breaks the direct correspondence with a real-even DFT of half-shifted input. This is the normalization used by Matlab.[99] In many applications, such as JPEG, the scaling is arbitrary because scale factors can be combined with a subsequent computational step (e.g. the quantization step in JPEG[100]), and a scaling can be chosen that allows the DCT to be computed with fewer multiplications.[101][102]
The DCT-II implies the boundary conditions: is even around and even around ; is even around and odd around .
DCT-III
Because it is the inverse of DCT-II up to a scale factor (see below), this form is sometimes simply referred to as the inverse DCT (IDCT).[6]
Some authors divide the term by instead of by 2 (resulting in an overall term) and multiply the resulting matrix by an overall scale factor of (see above for the corresponding change in DCT-II), so that the DCT-II and DCT-III are transposes of one another. This makes the DCT-III matrix orthogonal, but breaks the direct correspondence with a real-even DFT of half-shifted output.
The DCT-III implies the boundary conditions: is even around and odd around is even around and even around
DCT-IV
The DCT-IV matrix becomes orthogonal (and thus, being clearly symmetric, its own inverse) if one further multiplies by an overall scale factor of
A variant of the DCT-IV, where data from different transforms are overlapped, is called the modified discrete cosine transform (MDCT).[103]
The DCT-IV implies the boundary conditions: is even around and odd around ; similarly for .
DCT V-VIII
DCTs of types I–IV treat both boundaries consistently regarding the point of symmetry: they are even or odd around either a data point for both boundaries or halfway between two data points for both boundaries. By contrast, DCTs of types V-VIII imply boundaries that are even or odd around a data point for one boundary and halfway between two data points for the other boundary.
In other words, DCT types I–IV are equivalent to real-even DFTs of even order (regardless of whether is even or odd), since the corresponding DFT is of length (for DCT-I) or (for DCT-II and III) or (for DCT-IV). The four additional types of discrete cosine transform[104] correspond essentially to real-even DFTs of logically odd order, which have factors of in the denominators of the cosine arguments.
However, these variants seem to be rarely used in practice. One reason, perhaps, is that FFT algorithms for odd-length DFTs are generally more complicated than FFT algorithms for even-length DFTs (e.g., the simplest radix-2 algorithms are only for even lengths), and this increased intricacy carries over to the DCTs as described below. Not that the trivial real-even array, a length-one DFT (odd length) of a single number , corresponds to a DCT-V of length .
Inverse transforms
Using the normalization conventions above, the inverse of DCT-I is DCT-I multiplied by 2/(N − 1). The inverse of DCT-IV is DCT-IV multiplied by 2/N. The inverse of DCT-II is DCT-III multiplied by 2/N and vice versa.[6]
Like for the DFT, the normalization factor in front of these transform definitions is merely a convention and differs between treatments. For example, some authors multiply the transforms by so that the inverse does not require any additional multiplicative factor. Combined with appropriate factors of √2 (see above), this can be used to make the transform matrix orthogonal.
Multidimensional DCTs
Multidimensional variants of the various DCT types follow straightforwardly from the one-dimensional definitions: they are simply a separable product (equivalently, a composition) of DCTs along each dimension.
M-D DCT-II
For example, a two-dimensional DCT-II of an image or a matrix is simply the one-dimensional DCT-II, from above, performed along the rows and then along the columns (or vice versa). The inverse of a multi-dimensional DCT is just a separable product of the inverses of the corresponding one-dimensional DCTs (see above), e.g., the one-dimensional inverses applied along one dimension at a time in a row-column algorithm.
The 2D DCT-II is given by the formula (omitting normalization and other scale factors, as above)
The 3-D DCT-II is only the extension of 2-D DCT-II in three-dimensional space and mathematically can be calculated by the formula
The inverse of 3-D DCT-II is 3-D DCT-III and can be computed from the formula
Technically, computing a two-, three- (or -multi) dimensional DCT by sequences of one-dimensional DCTs along each dimension is known as a row-column algorithm. As with multidimensional FFT algorithms, however, there exist other methods to compute the same thing while performing the computations in a different order (i.e., interleaving or combining the algorithms for the different dimensions). Owing to the rapid growth in the applications based on the 3-D DCT, several fast algorithms have been developed for the computation of 3-D DCT-II. Vector-Radix algorithms are applied for computing M-D DCT to reduce the computational complexity and to increase the computational speed. Vector-Radix Decimation in Frequency (VR DIF) is an example of an algorithm to compute a 3-D DCT-II efficiently.
3-D DCT-II VR DIF
In order to apply the VR DIF algorithm, the input data must be formulated and rearranged as follows.[105][106] The transform size N × N × N is assumed to be 2.

- where
The adjacent figure shows the four stages that are involved in calculating 3-D DCT-II using VR DIF algorithm. The first stage is the 3-D reordering using the index mapping illustrated by the above equations. The second stage is the butterfly calculation. Each butterfly calculates eight points together as shown in the figure just below, where .
The original 3-D DCT-II can now be written as
- where
If the even and the odd parts of and are considered, the general formula for the calculation of the 3-D DCT-II can be expressed as

- where
Arithmetic complexity
The whole 3-D DCT calculation needs stages, and each stage involves butterflies. The whole 3-D DCT requires butterflies to be computed. Each butterfly requires seven real multiplications (including trivial multiplications) and 24 real additions (including trivial additions). Therefore, the total number of real multiplications needed for this stage is and the total number of real additions i.e. including the post-additions (recursive additions) which can be calculated directly after the butterfly stage or after the bit-reverse stage are given by[106]
The conventional method to calculate MD-DCT-II is using a Row-Column-Frame (RCF) approach which is computationally complex and less productive on most advanced recent hardware platforms. The number of multiplications required to compute VR DIF Algorithm when compared to RCF algorithm are quite a few in number. The number of Multiplications and additions involved in RCF approach are given by and respectively. From Table 1, it can be seen that the total number
| Transform Size | 3D VR Mults | RCF Mults | 3D VR Adds | RCF Adds |
|---|---|---|---|---|
| 8 × 8 × 8 | 2.625 | 4.5 | 10.875 | 10.875 |
| 16 × 16 × 16 | 3.5 | 6 | 15.188 | 15.188 |
| 32 × 32 × 32 | 4.375 | 7.5 | 19.594 | 19.594 |
| 64 × 64 × 64 | 5.25 | 9 | 24.047 | 24.047 |
of multiplications associated with the 3-D DCT VR algorithm is less than that associated with the RCF approach by more than 40%. In addition, the RCF approach involves matrix transpose and more indexing and data swapping than the new VR algorithm. This makes the 3-D DCT VR algorithm more efficient and better suited for 3-D applications that involve the 3-D DCT-II such as video compression and other 3-D image processing applications.
The main consideration in choosing a fast algorithm is to avoid computational and structural complexities. As the technology of computers and DSPs advances, the execution time of arithmetic operations (multiplications and additions) is becoming very fast, and regular computational structure becomes the most important factor.[107] Therefore, although the above proposed 3-D VR algorithm does not achieve the theoretical lower bound on the number of multiplications,[108] it has a simpler computational structure as compared to other 3-D DCT algorithms. It can be implemented in place using a single butterfly and possesses the properties of the Cooley–Tukey FFT algorithm in 3-D. Hence, the 3-D VR presents a good choice for reducing arithmetic operations in the calculation of the 3-D DCT-II, while keeping the simple structure that characterize butterfly-style Cooley–Tukey FFT algorithms.
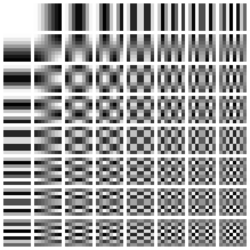
The image to the right shows a combination of horizontal and vertical frequencies for an 8 × 8 two-dimensional DCT. Each step from left to right and top to bottom is an increase in frequency by 1/2 cycle. For example, moving right one from the top-left square yields a half-cycle increase in the horizontal frequency. Another move to the right yields two half-cycles. A move down yields two half-cycles horizontally and a half-cycle vertically. The source data ( 8×8 ) is transformed to a linear combination of these 64 frequency squares.
MD-DCT-IV
The M-D DCT-IV is just an extension of 1-D DCT-IV on to M dimensional domain. The 2-D DCT-IV of a matrix or an image is given by
- for and
We can compute the MD DCT-IV using the regular row-column method or we can use the polynomial transform method[109] for the fast and efficient computation. The main idea of this algorithm is to use the Polynomial Transform to convert the multidimensional DCT into a series of 1-D DCTs directly. MD DCT-IV also has several applications in various fields.
Computation
Although the direct application of these formulas would require operations, it is possible to compute the same thing with only complexity by factorizing the computation similarly to the fast Fourier transform (FFT). One can also compute DCTs via FFTs combined with pre- and post-processing steps. In general, methods to compute DCTs are known as fast cosine transform (FCT) algorithms.
The most efficient algorithms, in principle, are usually those that are specialized directly for the DCT, as opposed to using an ordinary FFT plus extra operations (see below for an exception). However, even "specialized" DCT algorithms (including all of those that achieve the lowest known arithmetic counts, at least for power-of-two sizes) are typically closely related to FFT algorithms – since DCTs are essentially DFTs of real-even data, one can design a fast DCT algorithm by taking an FFT and eliminating the redundant operations due to this symmetry. This can even be done automatically (Frigo Johnson). Algorithms based on the Cooley–Tukey FFT algorithm are most common, but any other FFT algorithm is also applicable. For example, the Winograd FFT algorithm leads to minimal-multiplication algorithms for the DFT, albeit generally at the cost of more additions, and a similar algorithm was proposed by (Feig Winograd) for the DCT. Because the algorithms for DFTs, DCTs, and similar transforms are all so closely related, any improvement in algorithms for one transform will theoretically lead to immediate gains for the other transforms as well (Duhamel Vetterli).
While DCT algorithms that employ an unmodified FFT often have some theoretical overhead compared to the best specialized DCT algorithms, the former also have a distinct advantage: Highly optimized FFT programs are widely available. Thus, in practice, it is often easier to obtain high performance for general lengths N with FFT-based algorithms.[lower-alpha 3] Specialized DCT algorithms, on the other hand, see widespread use for transforms of small, fixed sizes such as the 8 × 8 DCT-II used in JPEG compression, or the small DCTs (or MDCTs) typically used in audio compression. (Reduced code size may also be a reason to use a specialized DCT for embedded-device applications.)
In fact, even the DCT algorithms using an ordinary FFT are sometimes equivalent to pruning the redundant operations from a larger FFT of real-symmetric data, and they can even be optimal from the perspective of arithmetic counts. For example, a type-II DCT is equivalent to a DFT of size with real-even symmetry whose even-indexed elements are zero. One of the most common methods for computing this via an FFT (e.g. the method used in FFTPACK and FFTW) was described by (Narasimha Peterson) and (Makhoul 1980), and this method in hindsight can be seen as one step of a radix-4 decimation-in-time Cooley–Tukey algorithm applied to the "logical" real-even DFT corresponding to the DCT-II.[lower-alpha 4] Because the even-indexed elements are zero, this radix-4 step is exactly the same as a split-radix step. If the subsequent size real-data FFT is also performed by a real-data split-radix algorithm (as in (Sorensen Jones)), then the resulting algorithm actually matches what was long the lowest published arithmetic count for the power-of-two DCT-II ( real-arithmetic operations[lower-alpha 5]).
A recent reduction in the operation count to also uses a real-data FFT.[110] So, there is nothing intrinsically bad about computing the DCT via an FFT from an arithmetic perspective – it is sometimes merely a question of whether the corresponding FFT algorithm is optimal. (As a practical matter, the function-call overhead in invoking a separate FFT routine might be significant for small but this is an implementation rather than an algorithmic question since it can be solved by unrolling or inlining.)
Example of IDCT

Consider this 8 × 8 grayscale image of capital letter A.
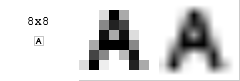

DCT of the image = .
Each basis function is multiplied by its coefficient and then this product is added to the final image.

See also
- Discrete wavelet transform
- JPEG - Discrete cosine transform - Contains a potentially easier to understand example of DCT transformation
- List of Fourier-related transforms
- Modified discrete cosine transform
Notes
- ↑ Here, we think of the DFT or DCT as approximations for the Fourier series or cosine series of a function, respectively, in order to talk about its smoothness.
- ↑ A similar problem arises for the DST, in which the odd left boundary condition implies a discontinuity for any function that does not happen to be zero at that boundary.
- ↑ Algorithmic performance on modern hardware is typically not principally determined by simple arithmetic counts, and optimization requires substantial engineering effort to make best use, within its intrinsic limits, of available built-in hardware optimization.
- ↑ The radix-4 step reduces the size DFT to four size DFTs of real data, two of which are zero, and two of which are equal to one another by the even symmetry. Hence giving a single size FFT of real data plus butterflies, once the trivial and / or duplicate parts are eliminated and / or merged.
- ↑ The precise count of real arithmetic operations, and in particular the count of real multiplications, depends somewhat on the scaling of the transform definition. The count is for the DCT-II definition shown here; two multiplications can be saved if the transform is scaled by an overall factor. Additional multiplications can be saved if one permits the outputs of the transform to be rescaled individually, as was shown by (Arai Agui) for the size-8 case used in JPEG.
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 1.25 1.26 Stanković, Radomir S.; Astola, Jaakko T. (2012). "Reminiscences of the Early Work in DCT: Interview with K.R. Rao". Reprints from the Early Days of Information Sciences (Tampere International Center for Signal Processing) 60. ISBN 978-952-15-2818-7. ISSN 1456-2774. https://ethw.org/w/images/1/19/Report-60.pdf. Retrieved 2021-12-30.
- ↑ 2.0 2.1 2.2 2.3 2.4 Britanak, Vladimir; Yip, Patrick C.; Rao, K. R. (2006-11-06) (in en). Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations. Academic Press. ISBN 978-0-12-373624-6. OCLC 220853454.
- ↑ 3.0 3.1 3.2 3.3 Alikhani, Darya (April 1, 2015). "Beyond resolution: Rosa Menkman's glitch art". http://postmatter.merimedia.com/articles/archive-2012-2016/2015/51-rosa-menkman/.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 Thomson, Gavin; Shah, Athar (2017). "Introducing HEIF and HEVC". Apple Inc.. https://devstreaming-cdn.apple.com/videos/wwdc/2017/503i6plfvfi7o3222/503/503_introducing_heif_and_hevc.pdf.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Ahmed, Nasir; Natarajan, T. Raj; Rao, K.R. (1974-01-01). "Discrete Cosine Transform" (in en). IEEE Transactions on Computers (IEEE Computer Society) C-23 (1): 90-93. doi:10.1109/T-C.1974.223784. ISSN 0018-9340. OCLC 1799331. Bibcode: 1974ITCmp.100...90A.
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 Rao, K. Ramamohan; Yip, Patrick C. (1990-09-11) (in en). Discrete Cosine Transform: Algorithms, Advantages, Applications. Signal, Image and Speech Processing. Academic Press. doi:10.1016/c2009-0-22279-3. ISBN 978-0-12-580203-1. OCLC 1008648293.
- ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 Barbero, M.; Hofmann, H.; Wells, N. D. (14 November 1991). "DCT source coding and current implementations for HDTV". EBU Technical Review (European Broadcasting Union) (251): 22–33. https://tech.ebu.ch/publications/trev_251-barbero. Retrieved 4 November 2019.
- ↑ 8.0 8.1 8.2 8.3 8.4 Lea, William (1994). "Video on demand: Research Paper 94/68". House of Commons Library. https://researchbriefings.parliament.uk/ResearchBriefing/Summary/RP94-68. Retrieved 20 September 2019.
- ↑ 9.0 9.1 Ahmed, Nasir (January 1991). "How I Came Up With the Discrete Cosine Transform". Digital Signal Processing 1 (1): 4–5. doi:10.1016/1051-2004(91)90086-Z. Bibcode: 1991DSP.....1....4A. https://www.cse.iitd.ac.in/~pkalra/col783-2017/DCT-History.pdf.
- ↑ 10.0 10.1 10.2 10.3 10.4 "T.81 – Digital compression and coding of continuous-tone still images – Requirements and guidelines". CCITT. September 1992. https://www.w3.org/Graphics/JPEG/itu-t81.pdf.
- ↑ Chen, Wen-Hsiung; Smith, C. H.; Fralick, S. C. (September 1977). "A Fast Computational Algorithm for the Discrete Cosine Transform". IEEE Transactions on Communications 25 (9): 1004–1009. doi:10.1109/TCOM.1977.1093941. Bibcode: 1977ITCom..25.1004W.
- ↑ Smith, C.; Fralick, S. (1977). "A Fast Computational Algorithm for the Discrete Cosine Transform". IEEE Transactions on Communications 25 (9): 1004–1009. doi:10.1109/TCOM.1977.1093941. ISSN 0090-6778. Bibcode: 1977ITCom..25.1004W.
- ↑ Dhamija, Swati; Jain, Priyanka (September 2011). "Comparative Analysis for Discrete Sine Transform as a suitable method for noise estimation". IJCSI International Journal of Computer Science 8 (5, No. 3): 162–164 (162). https://www.researchgate.net/publication/267228857. Retrieved 4 November 2019.
- ↑ Huang, T. S. (1981). Image Sequence Analysis. Springer Science & Business Media. p. 29. ISBN 978-3-642-87037-8. https://books.google.com/books?id=bAirCAAAQBAJ&pg=PA29.
- ↑ Roese, John A.; Robinson, Guner S. (30 October 1975). "Combined Spatial And Temporal Coding Of Digital Image Sequences". Efficient Transmission of Pictorial Information (International Society for Optics and Photonics) 0066: 172–181. doi:10.1117/12.965361. Bibcode: 1975SPIE...66..172R.
- ↑ Cianci, Philip J. (2014). High Definition Television: The Creation, Development and Implementation of HDTV Technology. McFarland. p. 63. ISBN 978-0-7864-8797-4. https://books.google.com/books?id=0mbsfr38GTgC&pg=PA63.
- ↑ 17.0 17.1 17.2 "History of Video Compression". Joint Video Team (JVT) of ISO/IEC MPEG & ITU-T VCEG (ISO/IEC JTC1/SC29/WG11 and ITU-T SG16 Q.6). July 2002. pp. 11, 24–9, 33, 40–1, 53–6. https://www.itu.int/wftp3/av-arch/jvt-site/2002_07_Klagenfurt/JVT-D068.doc.
- ↑ 18.0 18.1 18.2 Ghanbari, Mohammed (2003). Standard Codecs: Image Compression to Advanced Video Coding. Institution of Engineering and Technology. pp. 1–2. ISBN 978-0-85296-710-2. https://books.google.com/books?id=7XuU8T3ooOAC&pg=PA1.
- ↑ Li, Jian Ping (2006). Proceedings of the International Computer Conference 2006 on Wavelet Active Media Technology and Information Processing: Chongqing, China, 29-31 August 2006. World Scientific. p. 847. ISBN 978-981-270-999-8. https://books.google.com/books?id=FZiK3zXdK7sC&pg=PA847.
- ↑ Princen, John P.; Johnson, A.W.; Bradley, Alan B. (1987). "Subband/Transform coding using filter bank designs based on time domain aliasing cancellation". ICASSP '87. IEEE International Conference on Acoustics, Speech, and Signal Processing. 12. pp. 2161–2164. doi:10.1109/ICASSP.1987.1169405.
- ↑ Princen, J.; Bradley, A. (1986). "Analysis/Synthesis filter bank design based on time domain aliasing cancellation". IEEE Transactions on Acoustics, Speech, and Signal Processing 34 (5): 1153–1161. doi:10.1109/TASSP.1986.1164954. Bibcode: 1986ITASS..34.1153P.
- ↑ 22.00 22.01 22.02 22.03 22.04 22.05 22.06 22.07 22.08 22.09 22.10 Luo, Fa-Long (2008). Mobile Multimedia Broadcasting Standards: Technology and Practice. Springer Science & Business Media. p. 590. ISBN 978-0-387-78263-8. https://books.google.com/books?id=l6PovWat8SMC&pg=PA590.
- ↑ 23.0 23.1 Britanak, V. (2011). "On Properties, Relations, and Simplified Implementation of Filter Banks in the Dolby Digital (Plus) AC-3 Audio Coding Standards". IEEE Transactions on Audio, Speech, and Language Processing 19 (5): 1231–1241. doi:10.1109/TASL.2010.2087755. Bibcode: 2011ITASL..19.1231B.
- ↑ 24.0 24.1 Guckert, John (Spring 2012). "The Use of FFT and MDCT in MP3 Audio Compression". http://www.math.utah.edu/~gustafso/s2012/2270/web-projects/Guckert-audio-compression-svd-mdct-MP3.pdf.
- ↑ 25.0 25.1 Brandenburg, Karlheinz (1999). "MP3 and AAC Explained". http://graphics.ethz.ch/teaching/mmcom12/slides/mp3_and_aac_brandenburg.pdf.
- ↑ 26.0 26.1 Xiph.Org Foundation (2009-06-02). "Vorbis I specification - 1.1.2 Classification". Xiph.Org Foundation. http://www.xiph.org/vorbis/doc/Vorbis_I_spec.html#x1-50001.1.2.
- ↑ Mandyam, Giridhar D.; Ahmed, Nasir; Magotra, Neeraj (17 April 1995). "DCT-based scheme for lossless image compression". Digital Video Compression: Algorithms and Technologies 1995 (International Society for Optics and Photonics) 2419: 474–478. doi:10.1117/12.206386. Bibcode: 1995SPIE.2419..474M.
- ↑ Komatsu, K.; Sezaki, Kaoru (1998). "Reversible discrete cosine transform". Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP '98 (Cat. No.98CH36181). 3. pp. 1769–1772 vol.3. doi:10.1109/ICASSP.1998.681802. ISBN 0-7803-4428-6. https://www.researchgate.net/publication/3747502.
- ↑ Muchahary, D.; Mondal, A. J.; Parmar, R. S.; Borah, A. D.; Majumder, A. (2015). "A Simplified Design Approach for Efficient Computation of DCT". 2015 Fifth International Conference on Communication Systems and Network Technologies. pp. 483–487. doi:10.1109/CSNT.2015.134. ISBN 978-1-4799-1797-6.
- ↑ Chen, Wai Kai (2004). The Electrical Engineering Handbook. Elsevier. p. 906. ISBN 978-0-08-047748-0. https://books.google.com/books?id=qhHsSlazGrQC&pg=PA906.
- ↑ 31.0 31.1 31.2 "What Is a JPEG? The Invisible Object You See Every Day". 24 September 2013. https://www.theatlantic.com/technology/archive/2013/09/what-is-a-jpeg-the-invisible-object-you-see-every-day/279954/.
- ↑ 32.0 32.1 32.2 Pessina, Laure-Anne (12 December 2014). "JPEG changed our world". EPFL News (École Polytechnique Fédérale de Lausanne). https://actu.epfl.ch/news/jpeg-changed-our-world/.
- ↑ 33.0 33.1 Lee, Ruby Bei-Loh; Beck, John P.; Lamb, Joel; Severson, Kenneth E. (April 1995). "Real-time software MPEG video decoder on multimedia-enhanced PA 7100LC processors". Hewlett-Packard Journal 46 (2). ISSN 0018-1153. https://www.hpl.hp.com/hpjournal/95apr/apr95a7.pdf.
- ↑ 34.0 34.1 34.2 Lee, Jack (2005). Scalable Continuous Media Streaming Systems: Architecture, Design, Analysis and Implementation. John Wiley & Sons. p. 25. ISBN 978-0-470-85764-9. https://books.google.com/books?id=7fuvu52cyNEC&pg=PA25.
- ↑ 35.0 35.1 35.2 Shishikui, Yoshiaki; Nakanishi, Hiroshi; Imaizumi, Hiroyuki (October 26–28, 1993). "An HDTV Coding Scheme using Adaptive-Dimension DCT". Signal Processing of HDTV. Elsevier. pp. 611–618. doi:10.1016/B978-0-444-81844-7.50072-3. ISBN 978-1-4832-9851-1. https://books.google.com/books?id=j9XSBQAAQBAJ&pg=PA611.
- ↑ 36.0 36.1 Ochoa-Dominguez, Humberto; Rao, K. R. (2019). Discrete Cosine Transform, Second Edition. CRC Press. pp. 1–3, 129. ISBN 978-1-351-39648-6. https://books.google.com/books?id=dVOWDwAAQBAJ.
- ↑ 37.00 37.01 37.02 37.03 37.04 37.05 37.06 37.07 37.08 37.09 37.10 37.11 37.12 37.13 37.14 37.15 37.16 37.17 37.18 37.19 37.20 37.21 37.22 37.23 37.24 37.25 37.26 37.27 37.28 37.29 37.30 Ochoa-Dominguez, Humberto; Rao, K. R. (2019). Discrete Cosine Transform, Second Edition. CRC Press. pp. 1–3. ISBN 978-1-351-39648-6. https://books.google.com/books?id=dVOWDwAAQBAJ&pg=PA1.
- ↑ 38.0 38.1 38.2 38.3 38.4 Britanak, Vladimir; Rao, K. R. (2017). Cosine-/Sine-Modulated Filter Banks: General Properties, Fast Algorithms and Integer Approximations. Springer. p. 478. ISBN 978-3-319-61080-1. https://books.google.com/books?id=cZ4vDwAAQBAJ&pg=PA478.
- ↑ 39.0 39.1 Jones, Graham A.; Layer, David H.; Osenkowsky, Thomas G. (2013). National Association of Broadcasters Engineering Handbook: NAB Engineering Handbook. Taylor & Francis. pp. 558–9. ISBN 978-1-136-03410-7. https://books.google.com/books?id=K9N1TVhf82YC&pg=PA558.
- ↑ 40.0 40.1 40.2 Hersent, Olivier; Petit, Jean-Pierre; Gurle, David (2005). Beyond VoIP Protocols: Understanding Voice Technology and Networking Techniques for IP Telephony. John Wiley & Sons. p. 55. ISBN 978-0-470-02363-1. https://books.google.com/books?id=SMvNToRs-DgC&pg=PA55.
- ↑ 41.0 41.1 41.2 41.3 41.4 Daniel Eran Dilger (June 8, 2010). "Inside iPhone 4: FaceTime video calling". AppleInsider. http://www.appleinsider.com/articles/10/06/08/inside_iphone_4_facetime_video_calling.html.
- ↑ 42.0 42.1 42.2 42.3 Netflix Technology Blog (19 April 2017). "More Efficient Mobile Encodes for Netflix Downloads". Medium.com (Netflix). https://medium.com/netflix-techblog/more-efficient-mobile-encodes-for-netflix-downloads-625d7b082909.
- ↑ 43.0 43.1 "Video Developer Report 2019". 2019. https://cdn2.hubspot.net/hubfs/3411032/Bitmovin%20Magazine/Video%20Developer%20Report%202019/bitmovin-video-developer-report-2019.pdf.
- ↑ Ochoa-Dominguez, Humberto; Rao, K. R. (2019). Discrete Cosine Transform, Second Edition. CRC Press. p. 186. ISBN 978-1-351-39648-6. https://books.google.com/books?id=dVOWDwAAQBAJ&pg=PA186.
- ↑ 45.0 45.1 45.2 45.3 McKernan, Brian (2005). Digital cinema: the revolution in cinematography, postproduction, distribution. McGraw-Hill. p. 58. ISBN 978-0-07-142963-4. https://books.google.com/books?id=5vBTAAAAMAAJ. "DCT is used in most of the compression systems standardized by the Moving Picture Experts Group (MPEG), is the dominant technology for image compression. In particular, it is the core technology of MPEG-2, the system used for DVDs, digital television broadcasting, that has been used for many of the trials of digital cinema."
- ↑ 46.0 46.1 Baraniuk, Chris (15 October 2015). "Copy protections could come to JPegs". BBC News. BBC. https://www.bbc.co.uk/news/technology-34538705.
- ↑ Ascher, Steven; Pincus, Edward (2012). The Filmmaker's Handbook: A Comprehensive Guide for the Digital Age: Fifth Edition. Penguin. pp. 246–7. ISBN 978-1-101-61380-1. https://books.google.com/books?id=zp4KMKwnYVoC&pg=PA246.
- ↑ Bertalmio, Marcelo (2014). Image Processing for Cinema. CRC Press. p. 95. ISBN 978-1-4398-9928-1. https://books.google.com/books?id=6mnNBQAAQBAJ&pg=PA95.
- ↑ Zhang, HongJiang (1998). "Content-Based Video Browsing And Retrieval". Handbook of Internet and Multimedia Systems and Applications. CRC Press. pp. 83–108 (89). ISBN 978-0-8493-1858-0. https://books.google.com/books?id=5zfC1wI0wzUC&pg=PA89.
- ↑ 50.0 50.1 "Apple ProRes 422 Codec Family". 17 November 2014. http://www.loc.gov/preservation/digital/formats/fdd/fdd000389.shtml.
- ↑ Potluri, U. S.; Madanayake, A.; Cintra, R. J.; Bayer, F. M.; Rajapaksha, N. (17 October 2012). "Multiplier-free DCT approximations for RF multi-beam digital aperture-array space imaging and directional sensing". Measurement Science and Technology 23 (11). doi:10.1088/0957-0233/23/11/114003. ISSN 0957-0233.
- ↑ 52.0 52.1 Wang, Hanli; Kwong, S.; Kok, C. (2006). "Efficient prediction algorithm of integer DCT coefficients for H.264/AVC optimization". IEEE Transactions on Circuits and Systems for Video Technology 16 (4): 547–552. doi:10.1109/TCSVT.2006.871390. Bibcode: 2006ITCSV..16..547W.
- ↑ Hudson, Graham; Léger, Alain; Niss, Birger; Sebestyén, István; Vaaben, Jørgen (31 August 2018). "JPEG-1 standard 25 years: past, present, and future reasons for a success". Journal of Electronic Imaging 27 (4): 1. doi:10.1117/1.JEI.27.4.040901.
- ↑ "The JPEG image format explained". BT Group. 31 May 2018. https://home.bt.com/tech-gadgets/photography/what-is-a-jpeg-11364206889349.
- ↑ "HEIF Comparison - High Efficiency Image File Format". Nokia Technologies. https://nokiatech.github.io/heif/comparison.html.
- ↑ Alakuijala, Jyrki; Sneyers, Jon; Versari, Luca; Wassenberg, Jan (22 January 2021). "JPEG XL White Paper". http://ds.jpeg.org/whitepapers/jpeg-xl-whitepaper.pdf. "Variable-sized DCT (square or rectangular from 2x2 to 256x256) serves as a fast approximation of the optimal decorrelating transform."
- ↑ 57.0 57.1 Wang, Yao (2006). "Video Coding Standards: Part I". http://eeweb.poly.edu/~yao/EL6123/coding_standards_pt1.pdf.
- ↑ Wang, Yao (2006). "Video Coding Standards: Part II". http://eeweb.poly.edu/~yao/EL6123/coding_standards_pt2.pdf.
- ↑ Hoffman, Roy (2012). Data Compression in Digital Systems. Springer Science & Business Media. p. 255. ISBN 978-1-4615-6031-9. https://books.google.com/books?id=FOfTBwAAQBAJ.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedRao - ↑ Davis, Andrew (13 June 1997). "The H.320 Recommendation Overview". EE Times. https://www.eetimes.com/document.asp?doc_id=1275886.
- ↑ IEEE WESCANEX 97: communications, power, and computing: conference proceedings. University of Manitoba, Winnipeg, Manitoba, Canada: Institute of Electrical and Electronics Engineers. May 22–23, 1997. p. 30. ISBN 978-0-7803-4147-0. https://books.google.com/books?id=8vhEAQAAIAAJ. "H.263 is similar to, but more complex than H.261. It is currently the most widely used international video compression standard for video telephony on ISDN (Integrated Services Digital Network) telephone lines."
- ↑ Peter de Rivaz; Jack Haughton (2018). "AV1 Bitstream & Decoding Process Specification". Alliance for Open Media. https://aomediacodec.github.io/av1-spec/av1-spec.pdf.
- ↑ YouTube Developers (15 September 2018). "AV1 Beta Launch Playlist". https://www.youtube.com/playlist?list=PLyqf6gJt7KuHBmeVzZteZUlNUQAVLwrZS. "The first videos to receive YouTube's AV1 transcodes."
- ↑ Brinkmann, Martin (13 September 2018). "How to enable AV1 support on YouTube". https://www.ghacks.net/2018/09/13/how-to-enable-av1-support-on-youtube/.
- ↑ Netflix Technology Blog (5 February 2020). "Netflix Now Streaming AV1 on Android". https://netflixtechblog.com/netflix-now-streaming-av1-on-android-d5264a515202.
- ↑ Netflix Technology Blog (9 November 2021). "Bringing AV1 Streaming to Netflix Members' TVs". https://netflixtechblog.com/bringing-av1-streaming-to-netflix-members-tvs-b7fc88e42320.
- ↑ Herre, J.; Dietz, M. (2008). "MPEG-4 high-efficiency AAC coding [Standards in a Nutshell]". IEEE Signal Processing Magazine 25 (3): 137–142. doi:10.1109/MSP.2008.918684. Bibcode: 2008ISPM...25..137H.
- ↑ Valin, Jean-Marc; Maxwell, Gregory; Terriberry, Timothy B.; Vos, Koen (October 2013). "High-Quality, Low-Delay Music Coding in the Opus Codec". 135th AES Convention. Audio Engineering Society.
- ↑ "Opus Codec". Opus. Xiph.org Foundation. http://opus-codec.org/.
- ↑ Leyden, John (27 October 2015). "WhatsApp laid bare: Info-sucking app's innards probed". The Register. https://www.theregister.co.uk/2015/10/27/whatsapp_forensic_analysis/.
- ↑ Hazra, Sudip; Mateti, Prabhaker (September 13–16, 2017). "Challenges in Android Forensics". Security in Computing and Communications: 5th International Symposium, SSCC 2017. Springer. pp. 286–299 (290). doi:10.1007/978-981-10-6898-0_24. ISBN 978-981-10-6898-0. https://books.google.com/books?id=1u09DwAAQBAJ&pg=PA290.
- ↑ Srivastava, Saurabh Ranjan; Dube, Sachin; Shrivastaya, Gulshan; Sharma, Kavita (2019). "Smartphone Triggered Security Challenges - Issues, Case Studies and Prevention". Cyber Security in Parallel and Distributed Computing: Concepts, Techniques, Applications and Case Studies. John Wiley & Sons. pp. 187–206 (200). doi:10.1002/9781119488330.ch12. ISBN 978-1-119-48805-7. https://books.google.com/books?id=FzGtDwAAQBAJ&pg=PA200.
- ↑ "Open Source Software used in PlayStation 4". Sony Interactive Entertainment Inc.. https://doc.dl.playstation.net/doc/ps4-oss/.
- ↑ "Dolby AC-4: Audio Delivery for Next-Generation Entertainment Services". June 2015. https://www.dolby.com/us/en/technologies/ac-4/Next-Generation-Entertainment-Services.pdf.
- ↑ Bleidt, R. L. et al. (2017). "Development of the MPEG-H TV Audio System for ATSC 3.0". IEEE Transactions on Broadcasting 63 (1): 202–236. doi:10.1109/TBC.2017.2661258. Bibcode: 2017ITB....63..202B. https://www.iis.fraunhofer.de/content/dam/iis/en/doc/ame/Conference-Paper/BleidtR-IEEE-2017-Development-of-MPEG-H-TV-Audio-System-for-ATSC-3-0.pdf.
- ↑ Schnell, Markus; Schmidt, Markus; Jander, Manuel; Albert, Tobias; Geiger, Ralf; Ruoppila, Vesa; Ekstrand, Per; Bernhard, Grill (October 2008). "MPEG-4 Enhanced Low Delay AAC - A New Standard for High Quality Communication". 125th AES Convention. Audio Engineering Society. https://www.iis.fraunhofer.de/content/dam/iis/de/doc/ame/conference/AES-125-Convention_AAC-ELD-NewStandardForHighQualityCommunication_AES7503.pdf. Retrieved 20 October 2019.
- ↑ Lutzky, Manfred; Schuller, Gerald; Gayer, Marc; Krämer, Ulrich; Wabnik, Stefan (May 2004). "A guideline to audio codec delay". 116th AES Convention. Audio Engineering Society. https://www.iis.fraunhofer.de/content/dam/iis/de/doc/ame/conference/AES-116-Convention_guideline-to-audio-codec-delay_AES116.pdf. Retrieved 24 October 2019.
- ↑ 79.0 79.1 Nagireddi, Sivannarayana (2008). VoIP Voice and Fax Signal Processing. John Wiley & Sons. p. 69. ISBN 978-0-470-37786-4. https://books.google.com/books?id=5AneeZFE71MC&pg=PA69.
- ↑ "ITU-T Work Programme". https://www.itu.int/ITU-T/workprog/wp_item.aspx?isn=344.
- ↑ Terriberry, Timothy B. Presentation of the CELT codec. Event occurs at 65 minutes. Archived from the original on 2011-08-07. Retrieved 2019-10-19., also "CELT codec presentation slides". http://www.celt-codec.org/presentations/misc/lca-celt.pdf.
- ↑ "Ekiga 3.1.0 available". http://blog.ekiga.net/?p=112.
- ↑ "☏ FreeSWITCH". https://signalwire.com/freeswitch.
- ↑ "Enhanced Voice Services (EVS) Codec". Fraunhofer IIS. March 2017. https://www.iis.fraunhofer.de/content/dam/iis/de/doc/ame/wp/FraunhoferIIS_Technical-Paper_EVS.pdf.
- ↑ Abousleman, G. P.; Marcellin, M. W.; Hunt, B. R. (January 1995), "Compression of hyperspectral imagery using 3-D DCT and hybrid DPCM/DCT", IEEE Trans. Geosci. Remote Sens. 33 (1): 26–34, doi:10.1109/36.368225, Bibcode: 1995ITGRS..33...26A
- ↑ Chan, Y.; Siu, W. (May 1997), "Variable temporal-length 3-D discrete cosine transform coding", IEEE Trans. Image Process. 6 (5): 758–763, doi:10.1109/83.568933, PMID 18282969, Bibcode: 1997ITIP....6..758C, http://www.en.polyu.edu.hk/~wcsiu/paper_store/Journal/1997/1997_J3-IEEE-Chan%26Siu.pdf
- ↑ Song, J.; SXiong, Z.; Liu, X.; Liu, Y., "An algorithm for layered video coding and transmission", Proc. Fourth Int. Conf./Exh. High Performance Comput. Asia-Pacific Region 2: 700–703
- ↑ Tai, S.-C; Gi, Y.; Lin, C.-W. (September 2000), "An adaptive 3-D discrete cosine transform coder for medical image compression", IEEE Trans. Inf. Technol. Biomed. 4 (3): 259–263, doi:10.1109/4233.870036, PMID 11026596, Bibcode: 2000ITITB...4..259S
- ↑ Yeo, B.; Liu, B. (May 1995), "Volume rendering of DCT-based compressed 3D scalar data", IEEE Transactions on Visualization and Computer Graphics 1 (1): 29–43, doi:10.1109/2945.468390, Bibcode: 1995ITVCG...1...29B
- ↑ Chan, S.C.; Liu, W.; Ho, K.I. (2000). "Perfect reconstruction modulated filter banks with sum of powers-of-two coefficients". 2000 IEEE International Symposium on Circuits and Systems. Emerging Technologies for the 21st Century. Proceedings (IEEE Cat No.00CH36353). 2. pp. 73–76. doi:10.1109/ISCAS.2000.856261. ISBN 0-7803-5482-6.
- ↑ Queiroz, R. L.; Nguyen, T. Q. (1996). "Lapped transforms for efficient transform/subband coding". IEEE Trans. Signal Process. 44 (5): 497–507.
- ↑ Malvar 1992.
- ↑ Chan, S. C.; Luo, L.; Ho, K. L. (1998). "M-Channel compactly supported biorthogonal cosine-modulated wavelet bases". IEEE Trans. Signal Process. 46 (2): 1142–1151. doi:10.1109/78.668566. Bibcode: 1998ITSP...46.1142C.
- ↑ 94.0 94.1 Katsaggelos, Aggelos K.; Babacan, S. Derin; Chun-Jen, Tsai (2009). "Chapter 15 - Iterative Image Restoration". The Essential Guide to Image Processing. Academic Press. pp. 349–383. ISBN 978-0-12-374457-9.
- ↑ "Mosquito noise". https://www.pcmag.com/encyclopedia/term/55914/mosquito-noise.
- ↑ Menkman, Rosa (October 2011). The Glitch Moment(um). Institute of Network Cultures. ISBN 978-90-816021-6-7. https://networkcultures.org/_uploads/NN%234_RosaMenkman.pdf. Retrieved 19 October 2019.
- ↑ Ruff, Thomas (May 31, 2009). "jpegs". Aperture. Aperture. p. 132. ISBN 978-1-59711-093-8.
- ↑ Colberg, Jörg (April 17, 2009). "Review: jpegs by Thomas Ruff". http://jmcolberg.com/weblog/2009/04/review_jpegs_by_thomas_ruff/.
- ↑ "Discrete cosine transform - MATLAB dct". https://www.mathworks.com/help/signal/ref/dct.html.
- ↑ Pennebaker, William B.; Mitchell, Joan L. (31 December 1992). JPEG: Still Image Data Compression Standard. Springer. ISBN 978-0-442-01272-4.
- ↑ Arai, Y.; Agui, T.; Nakajima, M. (1988). "A fast DCT-SQ scheme for images". IEICE Transactions 71 (11): 1095–1097. https://search.ieice.org/bin/summary.php?id=e71-e_11_1095.
- ↑ Shao, Xuancheng; Johnson, Steven G. (2008). "Type-II/III DCT/DST algorithms with reduced number of arithmetic operations". Signal Processing 88 (6): 1553–1564. doi:10.1016/j.sigpro.2008.01.004. Bibcode: 2008SigPr..88.1553S.
- ↑ Malvar 1992
- ↑ Martucci 1994
- ↑ Chan, S.C.; Ho, K.L. (1990). "Direct methods for computing discrete sinusoidal transforms". IEE Proceedings F - Radar and Signal Processing 137 (6): 433. doi:10.1049/ip-f-2.1990.0063.
- ↑ 106.0 106.1 Alshibami, O.; Boussakta, S. (July 2001). "Three-dimensional algorithm for the 3-D DCT-III". Proc. Sixth Int. Symp. Commun., Theory Applications: 104–107.
- ↑ Guoan Bi; Gang Li; Kai-Kuang Ma; Tan, T.C. (2000). "On the computation of two-dimensional DCT". IEEE Transactions on Signal Processing 48 (4): 1171–1183. doi:10.1109/78.827550. Bibcode: 2000ITSP...48.1171B.
- ↑ Feig, E.; Winograd, S. (July 1992a). "On the multiplicative complexity of discrete cosine transforms". IEEE Transactions on Information Theory 38 (4): 1387–1391. doi:10.1109/18.144722. Bibcode: 1992ITIT...38.1387F.
- ↑ Nussbaumer, H.J. (1981). Fast Fourier transform and convolution algorithms (1st ed.). New York: Springer-Verlag.
- ↑ Shao, Xuancheng; Johnson, Steven G. (2008). "Type-II/III DCT/DST algorithms with reduced number of arithmetic operations". Signal Processing 88 (6): 1553–1564. doi:10.1016/j.sigpro.2008.01.004. Bibcode: 2008SigPr..88.1553S.
Further reading
- Narasimha, M.; Peterson, A. (June 1978). "On the Computation of the Discrete Cosine Transform". IEEE Transactions on Communications 26 (6): 934–936. doi:10.1109/TCOM.1978.1094144. Bibcode: 1978ITCom..26..934N.
- Makhoul, J. (February 1980). "A fast cosine transform in one and two dimensions". IEEE Transactions on Acoustics, Speech, and Signal Processing 28 (1): 27–34. doi:10.1109/TASSP.1980.1163351. Bibcode: 1980ITASS..28...27M.
- Sorensen, H.; Jones, D.; Heideman, M.; Burrus, C. (June 1987). "Real-valued fast Fourier transform algorithms". IEEE Transactions on Acoustics, Speech, and Signal Processing 35 (6): 849–863. doi:10.1109/TASSP.1987.1165220. Bibcode: 1987ITASS..35..849S.
- Plonka, G.; Tasche, M. (January 2005). "Fast and numerically stable algorithms for discrete cosine transforms". Linear Algebra and Its Applications 394 (1): 309–345. doi:10.1016/j.laa.2004.07.015.
- Duhamel, P.; Vetterli, M. (April 1990). "Fast fourier transforms: A tutorial review and a state of the art". Signal Processing 19 (4): 259–299. doi:10.1016/0165-1684(90)90158-U. Bibcode: 1990SigPr..19..259D. http://infoscience.epfl.ch/record/59946.
- Ahmed, N. (January 1991). "How I came up with the discrete cosine transform". Digital Signal Processing 1 (1): 4–9. doi:10.1016/1051-2004(91)90086-Z. Bibcode: 1991DSP.....1....4A. https://www.scribd.com/doc/52879771/DCT-History-How-I-Came-Up-with-the-Discrete-Cosine-Transform.
- Feig, E.; Winograd, S. (September 1992b). "Fast algorithms for the discrete cosine transform". IEEE Transactions on Signal Processing 40 (9): 2174–2193. doi:10.1109/78.157218. Bibcode: 1992ITSP...40.2174F.
- Malvar, Henrique (1992), Signal Processing with Lapped Transforms, Boston: Artech House, ISBN 978-0-89006-467-2
- Martucci, S. A. (May 1994). "Symmetric convolution and the discrete sine and cosine transforms". IEEE Transactions on Signal Processing 42 (5): 1038–1051. doi:10.1109/78.295213. Bibcode: 1994ITSP...42.1038M.
- Oppenheim, Alan; Schafer, Ronald; Buck, John (1999), Discrete-Time Signal Processing (2nd ed.), Upper Saddle River, N.J: Prentice Hall, ISBN 978-0-13-754920-7, https://archive.org/details/discretetimesign00alan
- Frigo, M.; Johnson, S. G. (February 2005). "The Design and Implementation of FFTW3". Proceedings of the IEEE 93 (2): 216–231. doi:10.1109/JPROC.2004.840301. Bibcode: 2005IEEEP..93..216F. http://fftw.org/fftw-paper-ieee.pdf.
- Boussakta, Said.; Alshibami, Hamoud O. (April 2004). "Fast Algorithm for the 3-D DCT-II". IEEE Transactions on Signal Processing 52 (4): 992–1000. doi:10.1109/TSP.2004.823472. Bibcode: 2004ITSP...52..992B. http://eprints.whiterose.ac.uk/708/1/boussaktas2.pdf.
- Cheng, L. Z.; Zeng, Y. H. (2003). "New fast algorithm for multidimensional type-IV DCT". IEEE Transactions on Signal Processing 51 (1): 213–220. doi:10.1109/TSP.2002.806558.
- Wen-Hsiung Chen; Smith, C.; Fralick, S. (September 1977). "A Fast Computational Algorithm for the Discrete Cosine Transform". IEEE Transactions on Communications 25 (9): 1004–1009. doi:10.1109/TCOM.1977.1093941. Bibcode: 1977ITCom..25.1004W.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 12.4.2. Cosine Transform", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=624, retrieved 2011-08-13
External links
- Syed Ali Khayam: The Discrete Cosine Transform (DCT): Theory and Application
- Implementation of MPEG integer approximation of 8x8 IDCT (ISO/IEC 23002-2)
- Matteo Frigo and Steven G. Johnson: FFTW, FFTW Home Page. A free (GPL) C library that can compute fast DCTs (types I-IV) in one or more dimensions, of arbitrary size.
- Takuya Ooura: General Purpose FFT Package, FFT Package 1-dim / 2-dim. Free C & FORTRAN libraries for computing fast DCTs (types II–III) in one, two or three dimensions, power of 2 sizes.
- Tim Kientzle: Fast algorithms for computing the 8-point DCT and IDCT, Algorithm Alley.
- LTFAT is a free Matlab/Octave toolbox with interfaces to the FFTW implementation of the DCTs and DSTs of type I-IV.
 |
