Discrete-time Fourier transform
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of discrete values.
The DTFT is often used to analyze samples of a continuous function. The term discrete-time refers to the fact that the transform operates on discrete data, often samples whose interval has units of time. From uniformly spaced samples it produces a function of frequency that is a periodic summation of the continuous Fourier transform of the original continuous function. In simpler terms, when you take the DTFT of regularly-spaced samples of a continuous signal, you get repeating (and possibly overlapping) copies of the signal's frequency spectrum, spaced at intervals corresponding to the sampling frequency. Under certain theoretical conditions, described by the sampling theorem, the original continuous function can be recovered perfectly from the DTFT and thus from the original discrete samples. The DTFT itself is a continuous function of frequency, but discrete samples of it can be readily calculated via the discrete Fourier transform (DFT) (see § Sampling the DTFT), which is by far the most common method of modern Fourier analysis.
Both transforms are invertible. The inverse DTFT reconstructs the original sampled data sequence, while the inverse DFT produces a periodic summation of the original sequence. The fast Fourier transform (FFT) is an algorithm for computing one cycle of the DFT, and its inverse produces one cycle of the inverse DFT.
Relation to Fourier Transform
Let be a continuous function in the time domain. We begin with a common definition of the continuous Fourier transform, where represents frequency in hertz and represents time in seconds:
We can reduce the integral into a summation by sampling at intervals of seconds (see Fourier transform § Numerical integration of a series of ordered pairs). Specifically, we can replace with a discrete sequence of its samples, , for integer values of , and replace the differential element with the sampling period . Thus, we obtain one formulation for the discrete-time Fourier transform (DTFT):
This Fourier series (in frequency) is a continuous periodic function, whose periodicity is the sampling frequency . The subscript distinguishes it from the continuous Fourier transform , and from the angular frequency form of the DTFT. The latter is obtained by defining an angular frequency variable, (which has normalized units of radians/sample), giving us a periodic function of angular frequency, with periodicity :[lower-alpha 1]
|
|
() |

The utility of the DTFT is rooted in the Poisson summation formula, which tells us that the periodic function represented by the Fourier series is a periodic summation of the continuous Fourier transform:[lower-alpha 2]
|
|
() |
The components of the periodic summation are centered at integer values (denoted by ) of a normalized frequency (cycles per sample). Ordinary/physical frequency (cycles per second) is the product of and the sample-rate, For sufficiently large the term can be observed in the region with little or no distortion (aliasing) from the other terms. Fig.1 depicts an example where is not large enough to prevent aliasing.
We also note that is the Fourier transform of Therefore, an alternative definition of DTFT is:[upper-alpha 1]
|
|
() |
The modulated Dirac comb function is a mathematical abstraction sometimes referred to as impulse sampling.[3]
Inverse transform
An operation that recovers the discrete data sequence from the DTFT function is called an inverse DTFT. For instance, the inverse continuous Fourier transform of both sides of Eq.3 produces the sequence in the form of a modulated Dirac comb function:
However, noting that is periodic, all the necessary information is contained within any interval of length In both Eq.1 and Eq.2, the summations over are a Fourier series, with coefficients The standard formulas for the Fourier coefficients are also the inverse transforms:
|
|
() |
Periodic data
When the input data sequence is -periodic, Eq.2 can be computationally reduced to a discrete Fourier transform (DFT), because:
- All the available information is contained within samples.
- converges to zero everywhere except at integer multiples of known as harmonic frequencies. At those frequencies, the DTFT diverges at different frequency-dependent rates. And those rates are given by the DFT of one cycle of the sequence.
- The DTFT is periodic, so the maximum number of unique harmonic amplitudes is
The DFT of one cycle of the sequence is:
And can be expressed in terms of the inverse transform, which is sometimes referred to as a Discrete Fourier series (DFS):[1]: p 542
With these definitions, we can demonstrate the relationship between the DTFT and the DFT:
Due to the -periodicity of both functions of this can be simplified to:
which satisfies the inverse transform requirement:
Sampling the DTFT
When the DTFT is continuous, a common practice is to compute an arbitrary number of samples of one cycle of the periodic function : [1]: pp 557–559 & 703 [2]: p 76
where is a periodic summation:
- (see Discrete Fourier series)
The sequence is the inverse DFT. Thus, our sampling of the DTFT causes the inverse transform to become periodic. The array of values is known as a periodogram, and the parameter is called NFFT in the Matlab function of the same name.[4]
In order to evaluate one cycle of numerically, we require a finite-length sequence. For instance, a long sequence might be truncated by a window function of length resulting in three cases worthy of special mention. For notational simplicity, consider the values below to represent the values modified by the window function.
Case: Frequency decimation. for some integer (typically 6 or 8)
A cycle of reduces to a summation of segments of length The DFT then goes by various names, such as:
- window-presum FFT[5]
- Weight, overlap, add (WOLA)[6][7][8][9][10][11][upper-alpha 3][upper-alpha 4]
Recall that decimation of sampled data in one domain (time or frequency) produces overlap (sometimes known as aliasing) in the other, and vice versa. Compared to an -length DFT, the summation/overlap causes decimation in frequency,[1]: p.558 leaving only DTFT samples least affected by spectral leakage. That is usually a priority when implementing an FFT filter-bank (channelizer). With a conventional window function of length scalloping loss would be unacceptable. So multi-block windows are created using FIR filter design tools.[14][15] Their frequency profile is flat at the highest point and falls off quickly at the midpoint between the remaining DTFT samples. The larger the value of parameter the better the potential performance.
Case:
When a symmetric, -length window function () is truncated by 1 coefficient it is called periodic or DFT-even. That is a common practice, but the truncation affects the DTFT (spectral leakage) by a small amount. It is at least of academic interest to characterize that effect. An -length DFT of the truncated window produces frequency samples at intervals of instead of The samples are real-valued,[16]: p.52 but their values do not exactly match the DTFT of the symmetric window. The periodic summation, along with an -length DFT, can also be used to sample the DTFT at intervals of Those samples are also real-valued and do exactly match the DTFT (example: :File:Sampling the Discrete-time Fourier transform.svg). To use the full symmetric window for spectral analysis at the spacing, one would combine the and data samples (by addition, because the symmetrical window weights them equally) and then apply the truncated symmetric window and the -length DFT.
Case: Frequency interpolation.
In this case, the DFT simplifies to a more familiar form:
In order to take advantage of a fast Fourier transform algorithm for computing the DFT, the summation is usually performed over all terms, even though of them are zeros. Therefore, the case is often referred to as zero-padding.
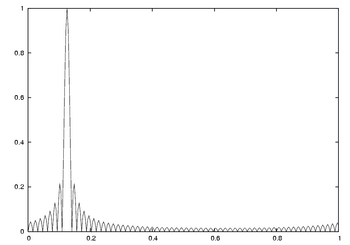
Spectral leakage, which increases as decreases, is detrimental to certain important performance metrics, such as resolution of multiple frequency components and the amount of noise measured by each DTFT sample. But those things don't always matter, for instance when the sequence is a noiseless sinusoid (or a constant), shaped by a window function. Then it is a common practice to use zero-padding to graphically display and compare the detailed leakage patterns of window functions. To illustrate that for a rectangular window, consider the sequence:
- and
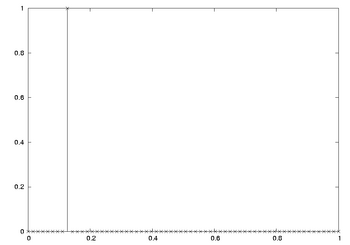
Figures 2 and 3 are plots of the magnitude of two different sized DFTs, as indicated in their labels. In both cases, the dominant component is at the signal frequency: . Also visible in Fig 2 is the spectral leakage pattern of the rectangular window. The illusion in Fig 3 is a result of sampling the DTFT at just its zero-crossings. Rather than the DTFT of a finite-length sequence, it gives the impression of an infinitely long sinusoidal sequence. Contributing factors to the illusion are the use of a rectangular window, and the choice of a frequency (1/8 = 8/64) with exactly 8 (an integer) cycles per 64 samples. A Hann window would produce a similar result, except the peak would be widened to 3 samples (see DFT-even Hann window).
Convolution
The convolution theorem for sequences is:
- [17]: p.297 [lower-alpha 4]
An important special case is the circular convolution of sequences s and y defined by where is a periodic summation. The discrete-frequency nature of means that the product with the continuous function is also discrete, which results in considerable simplification of the inverse transform:
For s and y sequences whose non-zero duration is less than or equal to N, a final simplification is:
The significance of this result is explained at Circular convolution and Fast convolution algorithms.
Relationship to the Z-transform
is a Fourier series that can also be expressed in terms of the bilateral Z-transform. I.e.:
where the notation distinguishes the Z-transform from the Fourier transform. Therefore, we can also express a portion of the Z-transform in terms of the Fourier transform:
Note that when parameter T changes, the terms of remain a constant separation apart, and their width scales up or down. The terms of S1/T(f) remain a constant width and their separation 1/T scales up or down.
Table of discrete-time Fourier transforms
Some common transform pairs are shown in the table below. The following notation applies:
- is a real number representing continuous angular frequency (in radians per sample). ( is in cycles/sec, and is in sec/sample.) In all cases in the table, the DTFT is 2π-periodic (in ).
- designates a function defined on .
- designates a function defined on , and zero elsewhere. Then:
- is the Dirac delta function
- is the normalized sinc function
- is the triangle function
- n is an integer representing the discrete-time domain (in samples)
- is the discrete-time unit step function
- is the Kronecker delta
| Time domain s[n] |
Frequency domain S2π(ω) |
Remarks | Reference |
|---|---|---|---|
| [17]: p.305 | |||
| integer | |||
odd M |
integer | ||
|
The term must be interpreted as a distribution in the sense of a Cauchy principal value around its poles at . | ||
| [17]: p.305 | |||
| -π < a < π
|
real number | ||
|
real number with | ||
| real number with | |||
| integer and odd integer | |||
| real numbers with | |||
| real number , | |||
| it works as a differentiator filter | |||
| real numbers with | |||
| Hilbert transform | |||
| 250px | real numbers complex |
Properties
This table shows some mathematical operations in the time domain and the corresponding effects in the frequency domain.
- is the discrete convolution of two sequences
- is the complex conjugate of
| Property | Time domain s[n] |
Frequency domain |
Remarks | Reference |
|---|---|---|---|---|
| Linearity | complex numbers | [17]: p.294 | ||
| Time reversal / Frequency reversal | [17]: p.297 | |||
| Time conjugation | [17]: p.291 | |||
| Time reversal & conjugation | [17]: p.291 | |||
| Real part in time | [17]: p.291 | |||
| Imaginary part in time | [17]: p.291 | |||
| Real part in frequency | [17]: p.291 | |||
| Imaginary part in frequency | [17]: p.291 | |||
| Shift in time / Modulation in frequency | integer k | [17]: p.296 | ||
| Shift in frequency / Modulation in time | real number | [17]: p.300 | ||
| Decimation | [upper-alpha 5] | integer | ||
| Time Expansion | integer | [1]: p.172 | ||
| Derivative in frequency | [17]: p.303 | |||
| Integration in frequency | ||||
| Differencing in time | ||||
| Summation in time | ||||
| Convolution in time / Multiplication in frequency | [17]: p.297 | |||
| Multiplication in time / Convolution in frequency | Periodic convolution | [17]: p.302 | ||
| Cross correlation | ||||
| Parseval's theorem | [17]: p.302 |
See also
Notes
- ↑ In fact Eq.2 is often justified as follows:[1]: p.143, eq 4.6
- ↑ From § Table of discrete-time Fourier transforms we have:
- ↑ WOLA should not be confused with the Overlap-add method of piecewise convolution.
- ↑ WOLA example: :File:WOLA channelizer example.png
- ↑ This expression is derived as follows:[1]: p.168
Page citations
- ↑ Oppenheim and Schafer,[1] p 147 (4.17), where: therefore
- ↑ Oppenheim and Schafer,[1] p 147 (4.20), p 694 (10.1), and Prandoni and Vetterli,[2] p 255, (9.33), where: and
- ↑ Oppenheim and Schafer,[1] p 551 (8.35), and Prandoni and Vetterli,[2] p 82, (4.43). With definitions: and this expression differs from the references by a factor of because they lost it in going from the 3rd step to the 4th. Specifically, the DTFT of at § Table of discrete-time Fourier transforms has a factor that the references omitted.
- ↑ Oppenheim and Schafer,[1] p 60, (2.169), and Prandoni and Vetterli,[2] p 122, (5.21)
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999). "4.2, 8.4". Discrete-time signal processing (2nd ed.). Upper Saddle River, N.J.: Prentice Hall. ISBN 0-13-754920-2. https://archive.org/details/discretetimesign00alan. "samples of the Fourier transform of an aperiodic sequence x[n] can be thought of as DFS coefficients of a periodic sequence obtained through summing periodic replicas of x[n]."
- ↑ 2.0 2.1 2.2 2.3 Prandoni, Paolo; Vetterli, Martin (2008). Signal Processing for Communications (1 ed.). Boca Raton, FL: CRC Press. pp. 72, 76. ISBN 978-1-4200-7046-0. https://www.sp4comm.org/docs/sp4comm.pdf. Retrieved 4 October 2020. "the DFS coefficients for the periodized signal are a discrete set of values for its DTFT"
- ↑ Rao, R. (2008). Signals and Systems. Prentice-Hall Of India Pvt. Limited. ISBN 9788120338593. https://books.google.com/books?id=4z3BrI717sMC.
- ↑ "Periodogram power spectral density estimate - MATLAB periodogram". https://www.mathworks.com/help/signal/ref/periodogram.html.
- ↑ Gumas, Charles Constantine (July 1997). "Window-presum FFT achieves high-dynamic range, resolution". Personal Engineering & Instrumentation News: 58–64. http://www.chipcenter.com/dsp/DSP000315F1.html.
- ↑ Crochiere, R.E.; Rabiner, L.R. (1983). "7.2". Multirate Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall. pp. 313–326. ISBN 0136051626. https://kupdf.net/download/multirate-digital-signal-processing-crochiere-rabiner_58a7065b6454a7e80bb1e993_pdf.
- ↑ Wang, Hong; Lu, Youxin; Wang, Xuegang (16 October 2006). "Channelized Receiver with WOLA Filterbank". 2006 CIE International Conference on Radar. Shanghai, China: IEEE. pp. 1–3. doi:10.1109/ICR.2006.343463. ISBN 0-7803-9582-4.
- ↑ Lyons, Richard G. (June 2008). "DSP Tricks: Building a practical spectrum analyzer". EE Times. https://www.embedded.com/dsp-tricks-building-a-practical-spectrum-analyzer. Note however, that it contains a link labeled weighted overlap-add structure which incorrectly goes to Overlap-add method.
- ↑ 9.0 9.1 Lillington, John (March 2003). "Comparison of Wideband Channelisation Architectures". Dallas: International Signal Processing Conference. p. 4 (fig 7). http://pdfs.semanticscholar.org/f3af/7acf516685ad04b3ebe19eb79db4dc3feb39.pdf. "The "Weight Overlap and Add" or WOLA or its subset the "Polyphase DFT", is becoming more established and is certainly very efficient where large, high quality filter banks are required."
- ↑ 10.0 10.1 Lillington, John. "A Review of Filter Bank Techniques - RF and Digital". Isle of Wight, UK: Libra Design Associates Ltd. p. 11. https://www.armms.org/media/uploads/16_lillington_a-review-of-filter-bank-techniques--.pdf. "Fortunately, there is a much more elegant solution, as shown in Figure 20 below, known as the Polyphase or WOLA (Weight, Overlap and Add) FFT."
- ↑ Hochgürtel, Stefan (2013), "2.5", Efficient implementations of high-resolution wideband FFT-spectrometers and their application to an APEX Galactic Center line survey, Bonn: Rhenish Friedrich Wilhelms University of Bonn, pp. 26–31, Bibcode: 2013PhDT.......427H, https://bonndoc.ulb.uni-bonn.de/xmlui/bitstream/handle/20.500.11811/5701/3251.pdf, retrieved 2024-09-19, "To perform M-fold WOLA for an N-point DFT, M·N real input samples aj first multiplied by a window function wj of same size"
- ↑ Chennamangalam, Jayanth (2016-10-18). "The Polyphase Filter Bank Technique". CASPER Group. https://casper.berkeley.edu/wiki/The_Polyphase_Filter_Bank_Technique.
- ↑ Dahl, Jason F. (2003-02-06). Time Aliasing Methods of Spectrum Estimation (Ph.D.). Brigham Young University. Retrieved 2016-10-31.
- ↑ Lin, Yuan-Pei; Vaidyanathan, P.P. (June 1998). "A Kaiser Window Approach for the Design of Prototype Filters of Cosine Modulated Filterbanks". IEEE Signal Processing Letters 5 (6): 132–134. doi:10.1109/97.681427. Bibcode: 1998ISPL....5..132L. http://authors.library.caltech.edu/6891/1/LINieeespl98.pdf. Retrieved 2017-03-16.
- ↑ Harris, Frederic J. (2004-05-24). "9". Multirate Signal Processing for Communication Systems. Upper Saddle River, NJ: Prentice Hall PTR. pp. 226–253. ISBN 0131465112.
- ↑ Harris, Fredric J. (Jan 1978). "On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform". Proceedings of the IEEE 66 (1): 51–83. doi:10.1109/PROC.1978.10837. Bibcode: 1978IEEEP..66...51H. http://web.mit.edu/xiphmont/Public/windows.pdf.
- ↑ 17.00 17.01 17.02 17.03 17.04 17.05 17.06 17.07 17.08 17.09 17.10 17.11 17.12 17.13 17.14 17.15 17.16 Proakis, John G.; Manolakis, Dimitri G. (1996) (in en). Digital Signal Processing: Principles, Algorithms and Applications (3 ed.). New Jersey: Prentice-Hall International. sAcfAQAAIAAJ. ISBN 9780133942897. Bibcode: 1996dspp.book.....P. https://archive.org/details/digitalsignalpro00proa.
- ↑ Rabiner, Lawrence R.; Gold, Bernard (1975). Theory and application of digital signal processing. Englewood Cliffs, NJ: Prentice-Hall, Inc.. p. 59 (2.163). ISBN 978-0139141010. https://archive.org/details/theoryapplicatio00rabi.
Further reading
- Porat, Boaz (1996). A Course in Digital Signal Processing. John Wiley and Sons. pp. 27–29 and 104–105. ISBN 0-471-14961-6.
- Siebert, William M. (1986). Circuits, Signals, and Systems. MIT Electrical Engineering and Computer Science Series. Cambridge, MA: MIT Press. ISBN 0262690950.
- Lyons, Richard G. (2010). Understanding Digital Signal Processing (3rd ed.). Prentice Hall. ISBN 978-0137027415.
 |
