Milstein method

Short description: Numerical method for solving stochastic differential equations

In mathematics, the Milstein method is a technique for the approximate numerical solution of a stochastic differential equation. It is named after Grigori N. Milstein who first published it in 1974.

Description

Consider the autonomous Itō stochastic differential equation: [math]\displaystyle{ \mathrm{d} X_t = a(X_t) \, \mathrm{d} t + b(X_t) \, \mathrm{d} W_t }[/math] with initial condition [math]\displaystyle{ X_{0} = x_{0} }[/math], where [math]\displaystyle{ W_{t} }[/math] stands for the Wiener process, and suppose that we wish to solve this SDE on some interval of time [math]\displaystyle{ [0,T] }[/math]. Then the Milstein approximation to the true solution [math]\displaystyle{ X }[/math] is the Markov chain [math]\displaystyle{ Y }[/math] defined as follows:

• partition the interval [math]\displaystyle{ [0,T] }[/math] into [math]\displaystyle{ N }[/math] equal subintervals of width [math]\displaystyle{ \Delta t\gt 0 }[/math]: [math]\displaystyle{ 0 = \tau_0 \lt \tau_1 \lt \dots \lt \tau_N = T\text{ with }\tau_n:=n\Delta t\text{ and }\Delta t = \frac{T}{N} }[/math]
• set [math]\displaystyle{ Y_0 = x_0; }[/math]
• recursively define [math]\displaystyle{ Y_n }[/math] for [math]\displaystyle{ 1 \leq n \leq N }[/math] by: [math]\displaystyle{ Y_{n + 1} = Y_n + a(Y_n) \Delta t + b(Y_n) \Delta W_n + \frac{1}{2} b(Y_n) b'(Y_n) \left( (\Delta W_n)^2 - \Delta t \right) }[/math] where [math]\displaystyle{ b' }[/math] denotes the derivative of [math]\displaystyle{ b(x) }[/math] with respect to [math]\displaystyle{ x }[/math] and: [math]\displaystyle{ \Delta W_n = W_{\tau_{n + 1}} - W_{\tau_n} }[/math] are independent and identically distributed normal random variables with expected value zero and variance [math]\displaystyle{ \Delta t }[/math]. Then [math]\displaystyle{ Y_n }[/math] will approximate [math]\displaystyle{ X_{\tau_n} }[/math] for [math]\displaystyle{ 0 \leq n \leq N }[/math], and increasing [math]\displaystyle{ N }[/math] will yield a better approximation.

Note that when [math]\displaystyle{ b'(Y_n) = 0 }[/math], i.e. the diffusion term does not depend on [math]\displaystyle{ X_{t} }[/math], this method is equivalent to the Euler–Maruyama method.

The Milstein scheme has both weak and strong order of convergence, [math]\displaystyle{ \Delta t }[/math], which is superior to the Euler–Maruyama method, which in turn has the same weak order of convergence, [math]\displaystyle{ \Delta t }[/math], but inferior strong order of convergence, [math]\displaystyle{ \sqrt{\Delta t} }[/math].

Intuitive derivation

For this derivation, we will only look at geometric Brownian motion (GBM), the stochastic differential equation of which is given by: [math]\displaystyle{ \mathrm{d} X_t = \mu X \mathrm{d} t + \sigma X d W_t }[/math] with real constants [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \sigma }[/math]. Using Itō's lemma we get: [math]\displaystyle{ \mathrm{d}\ln X_t= \left(\mu - \frac{1}{2} \sigma^2\right)\mathrm{d}t+\sigma\mathrm{d}W_t }[/math]

Thus, the solution to the GBM SDE is: [math]\displaystyle{ \begin{align} X_{t+\Delta t}&=X_t\exp\left\{\int_t^{t+\Delta t}\left(\mu-\frac{1}{2}\sigma^2\right)\mathrm{d}t+\int_t^{t+\Delta t}\sigma\mathrm{d}W_u\right\} \\ &\approx X_t\left(1+\mu\Delta t-\frac{1}{2} \sigma^2\Delta t+\sigma\Delta W_t+\frac{1}{2}\sigma^2(\Delta W_t)^2\right) \\ &= X_t + a(X_t)\Delta t+b(X_t)\Delta W_t+\frac{1}{2}b(X_t)b'(X_t)((\Delta W_t)^2-\Delta t) \end{align} }[/math] where [math]\displaystyle{ a(x) = \mu x, ~b(x) = \sigma x }[/math]

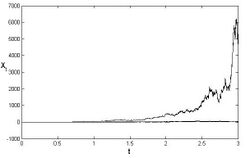
See numerical solution is presented above for three different trajectories.

Numerical solution for the stochastic differential equation just presented, the drift is twice the diffusion coefficient.

Computer implementation

The following Python code implements the Milstein method and uses it to solve the SDE describing the Geometric Brownian Motion defined by [math]\displaystyle{ \begin{cases} dY_t= \mu Y \, {\mathrm d}t + \sigma Y \, {\mathrm d}W_t \\ Y_0=Y_\text{init} \end{cases} }[/math]

# -*- coding: utf-8 -*-
# Milstein Method

import numpy as np
import matplotlib.pyplot as plt


class Model:
    """Stochastic model constants."""
    μ = 3
    σ = 1


def dW(Δt):
    """Random sample normal distribution."""
    return np.random.normal(loc=0.0, scale=np.sqrt(Δt))


def run_simulation():
    """ Return the result of one full simulation."""
    # One second and thousand grid points
    T_INIT = 0
    T_END = 1
    N = 1000 # Compute 1000 grid points
    DT = float(T_END - T_INIT) / N
    TS = np.arange(T_INIT, T_END + DT, DT)

    Y_INIT = 1

    # Vectors to fill
    ys = np.zeros(N + 1)
    ys[0] = Y_INIT
    for i in range(1, TS.size):
        t = (i - 1) * DT
        y = ys[i - 1]
        dw = dW(DT)

        # Sum up terms as in the Milstein method
        ys[i] = y + \
            Model.μ * y * DT + \
            Model.σ * y * dw + \
            (Model.σ**2 / 2) * y * (dw**2 - DT)

    return TS, ys


def plot_simulations(num_sims: int):
    """Plot several simulations in one image."""
    for _ in range(num_sims):
        plt.plot(*run_simulation())

    plt.xlabel("time (s)")
    plt.ylabel("y")
    plt.grid()
    plt.show()


if __name__ == "__main__":
    NUM_SIMS = 2
    plot_simulations(NUM_SIMS)

See also

• Euler–Maruyama method

Further reading

• Kloeden, P.E., & Platen, E. (1999). Numerical Solution of Stochastic Differential Equations. Springer, Berlin. ISBN 3-540-54062-8.