Nakagami distribution

Short description: Statistical distribution

Nakagami

Probability density function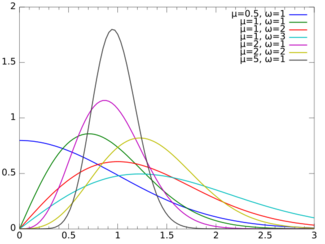
Cumulative distribution function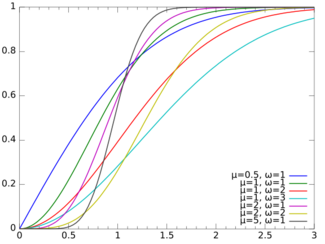
Parameters	[math]\displaystyle{ m\text{ or } \mu \geq 0.5 }[/math] shape (real) [math]\displaystyle{ \Omega \text{ or } \omega \gt 0 }[/math] spread (real)
Support	[math]\displaystyle{ x \gt 0\! }[/math]
PDF	[math]\displaystyle{ \frac{2m^m}{\Gamma(m)\Omega^m} x^{2m-1} \exp\left(-\frac{m}{\Omega}x^2 \right) }[/math]
CDF	[math]\displaystyle{ \frac{\gamma \left(m,\frac{m}{\Omega} x^2\right)}{\Gamma(m)} }[/math]
Mean	[math]\displaystyle{ \frac{\Gamma(m+\frac{1}{2})}{\Gamma(m)}\left(\frac{\Omega}{m}\right)^{1/2} }[/math]
Median	No simple closed form
Mode	[math]\displaystyle{ \left(\frac{(2m-1)\Omega}{2m}\right)^{1/2} }[/math]
Variance	[math]\displaystyle{ \Omega\left(1-\frac{1}{m}\left(\frac{\Gamma(m+\frac{1}{2})}{\Gamma(m)}\right)^2\right) }[/math]

The Nakagami distribution or the Nakagami-m distribution is a probability distribution related to the gamma distribution. It is used to model physical phenomena, such as those found in medical ultrasound imaging, communications engineering, meteorology, hydrology, multimedia, and seismology.

The family of Nakagami distributions has two parameters: a shape parameter [math]\displaystyle{ m\geq 1/2 }[/math] and a second parameter controlling spread [math]\displaystyle{ \Omega \gt 0 }[/math].

Characterization

Its probability density function (pdf) is

[math]\displaystyle{ f(x;\,m,\Omega) = \frac{2m^m}{\Gamma(m)\Omega^m}x^{2m-1}\exp\left(-\frac{m}{\Omega}x^2\right), \forall x\geq 0. }[/math]

where [math]\displaystyle{ m\geq 1/2 }[/math] and [math]\displaystyle{ \Omega\gt 0 }[/math].

Its cumulative distribution function (CDF) is

[math]\displaystyle{ F(x;\,m,\Omega) = \frac{\gamma\left(m, \frac{m}{\Omega}x^2\right)}{\Gamma(m)} = P\left(m, \frac{m}{\Omega}x^2\right) }[/math]

where P is the regularized (lower) incomplete gamma function.

Parameterization

The parameters [math]\displaystyle{ m }[/math] and [math]\displaystyle{ \Omega }[/math] are

[math]\displaystyle{ m = \frac{\left( \operatorname{E} \left[X^2 \right] \right)^2 } {\operatorname{Var} \left[X^2 \right]}, }[/math]

and

[math]\displaystyle{ \Omega = \operatorname{E} \left[X^2 \right]. }[/math]

No closed form solution exists for the median of this distribution, although special cases do exist, such as [math]\displaystyle{ \sqrt{\Omega \; ln(2)} }[/math] when m=1. For practical purposes the median would have to be calculated as the 50th-percentile of the observations.

Parameter estimation

An alternative way of fitting the distribution is to re-parametrize [math]\displaystyle{ \Omega }[/math] as σ = Ω/m.

Given independent observations [math]\displaystyle{ X_1=x_1,\ldots,X_n=x_n }[/math] from the Nakagami distribution, the likelihood function is

[math]\displaystyle{ L( \sigma, m) = \left( \frac{2}{\Gamma(m)\sigma^m} \right)^n \left( \prod_{i=1}^n x_i\right)^{2m-1} \exp\left(-\frac{\sum_{i=1}^n x_i^2} \sigma \right). }[/math]

Its logarithm is

[math]\displaystyle{ \ell(\sigma, m) = \log L(\sigma,m) = -n \log \Gamma(m) - nm\log\sigma + (2m-1) \sum_{i=1}^n \log x_i - \frac{ \sum_{i=1}^n x_i^2} \sigma. }[/math]

Therefore

[math]\displaystyle{ \begin{align} \frac{\partial\ell}{\partial\sigma} = \frac{-nm\sigma+\sum_{i=1}^n x_i^2}{\sigma^2} \quad \text{and} \quad \frac{\partial\ell}{\partial m} = -n\frac{\Gamma'(m)}{\Gamma(m)} -n \log\sigma + 2\sum_{i=1}^n \log x_i. \end{align} }[/math]

These derivatives vanish only when

[math]\displaystyle{ \sigma= \frac{\sum_{i=1}^n x_i^2}{nm} }[/math]

and the value of m for which the derivative with respect to m vanishes is found by numerical methods including the Newton–Raphson method.

It can be shown that at the critical point a global maximum is attained, so the critical point is the maximum-likelihood estimate of (m,σ). Because of the equivariance of maximum-likelihood estimation, a maximum likelihood estimate for Ω is obtained as well.

Random variate generation

The Nakagami distribution is related to the gamma distribution. In particular, given a random variable [math]\displaystyle{ Y \, \sim \textrm{Gamma}(k, \theta) }[/math], it is possible to obtain a random variable [math]\displaystyle{ X \, \sim \textrm{Nakagami} (m, \Omega) }[/math], by setting [math]\displaystyle{ k=m }[/math], [math]\displaystyle{ \theta=\Omega / m }[/math], and taking the square root of [math]\displaystyle{ Y }[/math]:

[math]\displaystyle{ X = \sqrt{Y}. \, }[/math]

Alternatively, the Nakagami distribution [math]\displaystyle{ f(y; \,m,\Omega) }[/math] can be generated from the chi distribution with parameter [math]\displaystyle{ k }[/math] set to [math]\displaystyle{ 2m }[/math] and then following it by a scaling transformation of random variables. That is, a Nakagami random variable [math]\displaystyle{ X }[/math] is generated by a simple scaling transformation on a Chi-distributed random variable [math]\displaystyle{ Y \sim \chi(2m) }[/math] as below.

[math]\displaystyle{ X = \sqrt{(\Omega / 2 m)Y} . }[/math]

For a Chi-distribution, the degrees of freedom [math]\displaystyle{ 2m }[/math] must be an integer, but for Nakagami the [math]\displaystyle{ m }[/math] can be any real number greater than 1/2. This is the critical difference and accordingly, Nakagami-m is viewed as a generalization of Chi-distribution, similar to a gamma distribution being considered as a generalization of Chi-squared distributions.

History and applications

The Nakagami distribution is relatively new, being first proposed in 1960 by Minoru Nakagami as a mathematical model for small-scale fading in long-distance high-frequency radio wave propagation. It has been used to model attenuation of wireless signals traversing multiple paths and to study the impact of fading channels on wireless communications.

Related distributions

• Restricting m to the unit interval (q = m; 0 < q < 1) defines the Nakagami-q distribution, also known as Hoyt distribution, first studied by R.S. Hoyt in the 1940s. In particular, the radius around the true mean in a bivariate normal random variable, re-written in polar coordinates (radius and angle), follows a Hoyt distribution. Equivalently, the modulus of a complex normal random variable also does.
• With 2m = k, the Nakagami distribution gives a scaled chi distribution.
• With [math]\displaystyle{ m = \tfrac 1 2 }[/math], the Nakagami distribution gives a scaled half-normal distribution.
• A Nakagami distribution is a particular form of generalized gamma distribution, with p = 2 and d = 2m.

See also

• Gamma distribution
• Modified half-normal distribution
• Sub-Gaussian distribution