No-three-in-line problem

From HandWiki
Short description: Geometry problem on grid points
A set of 20 points in a 10 × 10 grid, with no three points in a line.

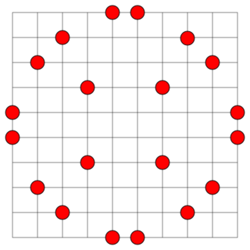
The no-three-in-line problem in discrete geometry asks how many points can be placed in the [math]\displaystyle{ n\times n }[/math] grid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".[1]

At most [math]\displaystyle{ 2n }[/math] points can be placed, because [math]\displaystyle{ 2n+1 }[/math] points in a grid would include a row of three or more points, by the pigeonhole principle. Although the problem can be solved with [math]\displaystyle{ 2n }[/math] points for every [math]\displaystyle{ n }[/math] up to [math]\displaystyle{ 46 }[/math], it is conjectured that fewer than [math]\displaystyle{ 2n }[/math] points can be placed in grids of large size. Known methods can place linearly many points in grids of arbitrary size, but the best of these methods place slightly fewer than [math]\displaystyle{ 3n/2 }[/math] points, not [math]\displaystyle{ 2n }[/math].

Several related problems of finding points with no three in line, among other sets of points than grids, have also been studied. Although originating in recreational mathematics, the no-three-in-line problem has applications in graph drawing and to the Heilbronn triangle problem.

Small instances

Solution to Dudeney's puzzle of placing 16 pawns on a chessboard such that no three pawns lie on the same line, and pawns are on squares d4 and e5

The problem was first posed by Henry Dudeney in 1900, as a puzzle in recreational mathematics, phrased in terms of placing the 16 pawns of a chessboard onto the board so that no three are in a line.[2] This is exactly the no-three-in-line problem, for the case [math]\displaystyle{ n=8 }[/math].[3] In a later version of the puzzle, Dudeney modified the problem, making its solution unique, by asking for a solution in which two of the pawns are on squares d4 and e5, attacking each other in the center of the board.[4]

Many authors have published solutions to this problem for small values of [math]\displaystyle{ n }[/math],[5] and by 1998 it was known that [math]\displaystyle{ 2n }[/math] points could be placed on an [math]\displaystyle{ n\times n }[/math] grid with no three in a line for all [math]\displaystyle{ n }[/math] up to 46, and some larger values.[6] The numbers of solutions with [math]\displaystyle{ 2n }[/math] points for small values of [math]\displaystyle{ n }[/math], starting from [math]\displaystyle{ n=2 }[/math], are

1, 2, 11, 32, 50, 132, 380, 368, 1135, 1120, 4348, 3622, 10568, ... (sequence A000755 in the OEIS).

The numbers of equivalence classes of solutions with [math]\displaystyle{ 2n }[/math] points under reflections and rotations are

1, 1, 4, 5, 11, 22, 57, 51, 156, 158, 566, 499, 1366, ... (sequence A000769 in the OEIS).[3]

Upper and lower bounds

The exact number of points that can be placed, as a function of [math]\displaystyle{ n }[/math], is not known. However, both proven and conjectured bounds limit this number to within a range proportional to [math]\displaystyle{ n }[/math].

General placement methods

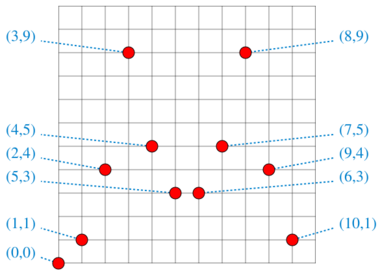
Suboptimal placement of [math]\displaystyle{ 11 }[/math] points in [math]\displaystyle{ 12\times 12 }[/math] grid, using the method of Erdős. The largest prime [math]\displaystyle{ p }[/math] less than the grid size is [math]\displaystyle{ p=11 }[/math]; the solution places points at coordinates [math]\displaystyle{ (i,i^2 }[/math] mod [math]\displaystyle{ p) }[/math] for [math]\displaystyle{ i=0,1,\dots p-1 }[/math]. For instance, [math]\displaystyle{ (4,5) }[/math] is included because [math]\displaystyle{ 4^2=16\cong 5 }[/math] ([math]\displaystyle{ }[/math]mod [math]\displaystyle{ 11 }[/math]).

A solution of Paul Erdős, published by (Roth 1951), is based on the observation that when [math]\displaystyle{ n }[/math] is a prime number, the set of [math]\displaystyle{ n }[/math] grid points [math]\displaystyle{ (i,i^2 }[/math] mod [math]\displaystyle{ n) }[/math], for [math]\displaystyle{ 0\le i \lt n }[/math], contains no three collinear points. When [math]\displaystyle{ n }[/math] is not prime, one can perform this construction for a [math]\displaystyle{ p\times p }[/math] grid contained in the [math]\displaystyle{ n\times n }[/math] grid, where [math]\displaystyle{ p }[/math] is the largest prime that is at most [math]\displaystyle{ n }[/math]. Because the gap between consecutive primes is much smaller than the primes themselves, [math]\displaystyle{ p }[/math] will always be close to [math]\displaystyle{ n }[/math], so this method can be used to place [math]\displaystyle{ n-o(n) }[/math] points in the [math]\displaystyle{ n\times n }[/math] grid with no three points collinear.[7]

Erdős' bound has been improved subsequently: (Hall Jackson) show that, when [math]\displaystyle{ n/2 }[/math] is prime, one can obtain a solution with [math]\displaystyle{ 3(n-2)/2 }[/math] points, by placing points in multiple copies of the hyperbola [math]\displaystyle{ xy=k }[/math] (mod [math]\displaystyle{ n/2 }[/math]), where [math]\displaystyle{ k }[/math] may be chosen arbitrarily as long as it is nonzero mod [math]\displaystyle{ n/2 }[/math]. Again, for arbitrary [math]\displaystyle{ n }[/math] one can perform this construction for a prime near [math]\displaystyle{ n/2 }[/math] to obtain a solution with [math]\displaystyle{ \tfrac32n-o(n) }[/math] points.[8]

Upper bound

At most [math]\displaystyle{ 2n }[/math] points may be placed in a grid of any size [math]\displaystyle{ n }[/math]. For, if more points are placed, then by the pigeonhole principle some three of them would all lie on the same horizontal line of the grid. For [math]\displaystyle{ n\leq 46 }[/math], this trivial bound is known to be tight.[3]

Conjectured bounds

Although exactly [math]\displaystyle{ 2n }[/math] points can be placed on small grids, (Guy Kelly) conjectured that for large grids, there is a significantly smaller upper bound on the number of points that can be placed. More precisely, they conjectured that the number of points that can be placed is at most a sublinear amount larger than [math]\displaystyle{ cn }[/math], with[9] [math]\displaystyle{ c = \sqrt[3]{\frac{2\pi^2}{3}} \approx 1.874. }[/math] After an error in the heuristic reasoning leading to this conjecture was uncovered, Guy corrected the error and made the stronger conjecture that one cannot do more than sublinearly better than [math]\displaystyle{ cn }[/math] with[10] [math]\displaystyle{ c = \frac{\pi}{\sqrt 3} \approx 1.814. }[/math]

Applications

Solutions to the no-three-in-line problem can be used to avoid certain kinds of degeneracies in graph drawing. The problem they apply to involves placing the vertices of a given graph at integer coordinates in the plane, and drawing the edges of the graph as straight line segments. For certain graphs, such as the utility graph, crossings between pairs of edges are unavoidable, but one should still avoid placements that cause a vertex to lie on an edge through two other vertices. When the vertices are placed with no three in line, this kind of problematic placement cannot occur, because the entire line through any two vertices, and not just the line segment, is free of other vertices.[11] The fact that the no-three-in-line problem has a solution with linearly many points can be translated into graph drawing terms as meaning that every graph, even a complete graph, can be drawn without unwanted vertex-edge incidences using a grid whose area is quadratic in the number of vertices, and that for complete graphs no such drawing with less than quadratic area is possible. The complete graphs also require a linear number of colors in any graph coloring, but other graphs that can be colored with fewer colors can also be drawn on smaller grids: if a graph has [math]\displaystyle{ n }[/math] vertices and a graph coloring with [math]\displaystyle{ k }[/math] colors, it can be drawn in a grid with area proportional to [math]\displaystyle{ nk }[/math]. The no-three-in-line drawing of a complete graph is a special case of this result with [math]\displaystyle{ k=n }[/math].[12]

The no-three-in-line problem also has applications to another problem in discrete geometry, the Heilbronn triangle problem. In this problem, one must place [math]\displaystyle{ n }[/math] points, anywhere in a unit square, not restricted to a grid. The goal of the placement is to avoid small-area triangles, and more specifically to maximize the area of the smallest triangle formed by three of the points. For instance, a placement with three points in line would be very bad by this criterion, because these three points would form a degenerate triangle with area zero. On the other hand, if the points can be placed on a grid of side length [math]\displaystyle{ \varepsilon }[/math] within the unit square, with no three in a line, then by Pick's theorem every triangle would have area at least [math]\displaystyle{ \varepsilon^2/2 }[/math], half of a grid square. Therefore, solving an instance of the no-three-in-line problem and then scaling down the integer grid to fit within a unit square produces solutions to the Heilbronn triangle problem where the smallest triangle has area [math]\displaystyle{ \Omega(1/n^2) }[/math]. This application was the motivation for Paul Erdős to find his solution for the no-three-in-line problem.[13] It remained the best area lower bound known for the Heilbronn triangle problem from 1951 until 1982, when it was improved by a logarithmic factor using a construction that was not based on the no-three-in-line problem.[14]

Generalizations and variations

General-position subsets

In computational geometry, finite sets of points with no three in line are said to be in general position. In this terminology, the no-three-in-line problem seeks the largest subset of a grid that is in general position, but researchers have also considered the problem of finding the largest general position subset of other non-grid sets of points. It is NP-hard to find this subset, for certain input sets, and hard to approximate its size to within a constant factor; this hardness of approximation result is summarized by saying that the problem is APX-hard. If the largest subset has size [math]\displaystyle{ k }[/math], a solution with the non-constant approximation ratio [math]\displaystyle{ O(\sqrt k) }[/math] can be obtained by a greedy algorithm that simply chooses points one at a time until all remaining points lie on lines through pairs of chosen points.[15]

One can get a finer-grained understanding of the running time of algorithms for finding the exact optimal solution by using parameterized complexity, in which algorithms are analyzed not only in terms of the input size, but in terms of other parameters of the input. In this case, for inputs whose largest general position subset has size [math]\displaystyle{ k }[/math], it can be found in an amount of time that is an exponential function of [math]\displaystyle{ k }[/math] multiplied by a polynomial in the input size [math]\displaystyle{ n }[/math], with the exponent of the polynomial not depending on [math]\displaystyle{ k }[/math]. Problems with this kind of time bound are called fixed-parameter tractable.[16]

For point sets [math]\displaystyle{ S }[/math] having at most [math]\displaystyle{ \ell }[/math] points per line, with [math]\displaystyle{ \ell=O(\sqrt{|S|}) }[/math], there exist general-position subsets of size nearly proportional to [math]\displaystyle{ \ell=O(\sqrt{|S|}) }[/math]. The example of the grid shows that this bound cannot be significantly improved.[17] The proof of existence of these large general-position subsets can be converted into a polynomial-time algorithm for finding a general-position subset of [math]\displaystyle{ S }[/math], of size matching the existence bound, using an algorithmic technique known as entropy compression.[15]

Greedy placement

Repeating a suggestion of (Adena Holton), Martin Gardner asked for the smallest subset of an [math]\displaystyle{ n\times n }[/math] grid that cannot be extended: it has no three points in a line, but every proper superset has three in a line. Equivalently, this is the smallest set that could be produced by a greedy algorithm that tries to solve the no-three-in-line problem by placing points one at a time until it gets stuck.[3] If only axis-parallel and diagonal lines are considered, then every such set has at least [math]\displaystyle{ n-1 }[/math] points.[18] However, less is known about the version of the problem where all lines are considered: every greedy placement includes at least [math]\displaystyle{ \Omega(n^{2/3}) }[/math] points before getting stuck, but nothing better than the trivial [math]\displaystyle{ 2n }[/math] upper bound is known.[19]

Higher dimensions

Non-collinear sets of points in the three-dimensional grid were considered by (Pór Wood). They proved that the maximum number of points in the [math]\displaystyle{ n\times n\times n }[/math] grid with no three points collinear is [math]\displaystyle{ \Theta(n^2) }[/math]. Similarly to Erdős's 2D construction, this can be accomplished by using points [math]\displaystyle{ (x,y,x^2+y^2 }[/math] mod [math]\displaystyle{ p) }[/math], where [math]\displaystyle{ p }[/math] is a prime congruent to 3 mod 4.[20] Just as the original no-three-in-line problem can be used for two-dimensional graph drawing, one can use this three-dimensional solution to draw graphs in the three-dimensional grid. Here the non-collinearity condition means that a vertex should not lie on a non-adjacent edge, but it is normal to work with the stronger requirement that no two edges cross.[21]

In much higher dimensions, sets of grid points with no three in line, obtained by choosing points near a hypersphere, have been used for finding large Salem–Spencer sets, sets of integers with no three forming an arithmetic progression.[22] However, it does not work well to use this same idea of choosing points near a circle in two dimensions: this method finds points forming convex polygons, which satisfy the requirement of having no three in line, but are too small. The largest convex polygons with vertices in an [math]\displaystyle{ n\times n }[/math] grid have only [math]\displaystyle{ O(n^{2/3}) }[/math] vertices.[23] The cap set problem concerns a similar problem to the no-three-in-line problem in spaces that are both high-dimensional, and based as vector spaces over finite fields rather than over the integers.[24]

Another generalization to higher dimensions is to find as many points as possible in a three dimensional [math]\displaystyle{ N \times N \times N }[/math] grid such that no four of them are in the same plane. This sequence begins 5, 8, 10, 13, 16, ... OEIS: A280537 for N = 2, 3, 4, etc.

Torus

Another variation on the problem involves converting the grid into a discrete torus by using periodic boundary conditions in which the left side of the torus is connected to the right side, and the top side is connected to the bottom side. This has the effect, on slanted lines through the grid, of connecting them up into longer lines through more points, and therefore making it more difficult to select points with at most two from each line. These extended lines can also be interpreted as normal lines through an infinite grid in the Euclidean plane, taken modulo the dimensions of the torus. For a torus based on an [math]\displaystyle{ m\times n }[/math] grid, the maximum number of points that can be chosen with no three in line is at most [math]\displaystyle{ 2\gcd(m,n) }[/math].[25] When both dimensions are equal, and prime, it is not possible to place exactly one point in each row and column without forming a linear number of collinear triples.[26] Higher-dimensional torus versions of the problem have also been studied.[27]

See also

  • Eight queens puzzle, on placing points on a grid with no two on the same row, column, or diagonal

Notes

  1. ↑ Brass, Moser & Pach 2005.
  2. ↑ The Weekly Dispatch, April 29 and May 13, 1900, as cited by Knuth 2008.
  3. ↑ 3.0 3.1 3.2 3.3 Gardner 1976.
  4. ↑ Dudeney 1917.
  5. ↑ Craggs & Hughes-Jones 1976; Kløve 1978, 1979; Anderson 1979; Harborth, Oertel & Prellberg 1989; Flammenkamp 1992, 1998.
  6. ↑ Flammenkamp 1992, 1998.
  7. ↑ Erdős did not publish this observation; it appears in Roth 1951.
  8. ↑ Hall et al. 1975.
  9. ↑ Guy & Kelly 1968.
  10. ↑ As reported by Pegg 2005. The discovery of this error was credited by Pegg to Gabor Ellmann.
  11. ↑ Brass et al. 2007.
  12. ↑ Wood 2005.
  13. ↑ Roth 1951.
  14. ↑ Komlós, Pintz & Szemerédi 1982.
  15. ↑ 15.0 15.1 Eppstein 2018.
  16. ↑ Froese et al. 2017; Eppstein 2018
  17. ↑ Payne & Wood 2013.
  18. ↑ Cooper et al. 2014.
  19. ↑ Aichholzer, Eppstein & Hainzl (2023).
  20. ↑ Pór & Wood 2007.
  21. ↑ Pach, Thiele & Tóth 1998; Dujmović, Morin & Wood 2005; Di Giacomo, Liotta & Meijer 2005
  22. ↑ Elkin 2011.
  23. ↑ Jarník 1926.
  24. ↑ Klarreich 2016.
  25. ↑ Misiak et al. 2016.
  26. ↑ Cooper & Solymosi 2005.
  27. ↑ Ku & Wong 2018.

References

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=No-three-in-line_problem&oldid=3376523"