One Clean Qubit

One clean qubit quantum circuit that estimates the trace of [math]\displaystyle{ U }[/math]

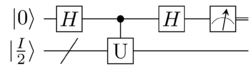
The One Clean Qubit model of computation is performed an [math]\displaystyle{ n }[/math] qubit system with one pure state and [math]\displaystyle{ n-1 }[/math] maximally mixed states. This model was motivated by highly mixed states that are prevalent in Nuclear magnetic resonance quantum computers. It's described by the density matrix [math]\displaystyle{ \rho = \left|0\right\rangle \langle 0| \otimes \frac{I}{2} }[/math], where I is the identity matrix. In computational complexity theory, DQC1; also known as the Deterministic quantum computation with one clean qubit is the class of decision problems solvable by a one clean qubit machine in polynomial time, upon measuring the first qubit, with an error probability of at most 1/poly(n) for all instances.

Error Bounds and Composability

The most standard definition of DQC1 requires that measuring the output qubit correctly accepts or rejects the input, with error at most [math]\displaystyle{ 1/q(n) }[/math] for specified some polynomial q, given a gap in acceptance probabilities of [math]\displaystyle{ [0,1/2-1/q(n)] }[/math] for NO instances and [math]\displaystyle{ [1/2+1/q(n),1] }[/math] for YES instances. Most probabilistic classes, such as BPP, BQP, and RP are agnostic to the precise probability gap, because any polynomial acceptance gap can be amplified to a fixed gap such as (1/3,2/3). A notable outlier is PP, which permits exponentially small gaps.

DQC1 does not admit an obvious notion of parallel composability or amplification: there is no clear construction to transform a circuit with, say, a (2/5,3/5) acceptance gap into a more accurate (1/5,4/5) acceptance gap.

It is known that DQC1 offers composability in the sense that the "one" clean qubit can be upgraded to "two" clean qubits, or even [math]\displaystyle{ log(n) }[/math] many clean qubits, without modifying the class Computation with Unitaries and One Pure Qubit. D. J. Shepherd.</ref> It is also not strengthened by measuring all of these clean qubits (as opposed to just the first clean qubit).

Relation to other classes

Because as many as [math]\displaystyle{ O(\log(n)) }[/math] qubits are permitted, DQC1 contains all logspace computations. It is closed under [math]\displaystyle{ \oplus }[/math]L reductions as well. It is not known to contain BPP or even P. It is contained in BQP, and it is conjectured that this is containment is strict.

It is known that simulating the sampling problem even for 3 output qubits is classically hard, in the sense that it would imply a PH collapse.

The term DQC1 has been used to instead refer to decision problems solved by a polynomial time classical circuit that adaptively makes queries to polynomially many DQC1 circuits. In this sense of use, the class naturally contains all of BPP, and the power of the class is focused on the "inherently quantum" power.

Trace Estimation

Trace estimation is complete for DQC1. Let [math]\displaystyle{ U }[/math] be a unitary [math]\displaystyle{ 2^n \times 2^n }[/math] matrix. Given a state [math]\displaystyle{ |\psi\rangle }[/math], the Hadamard test can estimate [math]\displaystyle{ \left\langle\psi\right| U \left|\psi\right\rangle }[/math] where [math]\displaystyle{ \frac{1}{2} + \frac{1}{2}\mathcal{Re}(\left\langle\psi\right| U \left|\psi\right\rangle) }[/math] is the probability that the measured clean qubit is 0. [math]\displaystyle{ I/2^n }[/math] mixed state inputs can be simulated by letting [math]\displaystyle{ |\psi\rangle }[/math] be chosen uniformly at random from [math]\displaystyle{ 2^{n} }[/math] computational basis states. When measured, the probability that the final result is 0 is [math]\displaystyle{ \frac{1}{2^n} \sum_{x \subset \{0, 1\}^n} \frac{1+\mathcal{Re}\left\langle x\right| U \left| x\right\rangle}{2} = \frac{1}{2} + \frac{1}{2} \frac{\mathcal{Re}(Tr(U))}{2^n} . }[/math] To estimate the imaginary part of the [math]\displaystyle{ Tr(U) }[/math], the clean qubit is initialized to [math]\displaystyle{ \frac{1}{\sqrt{2}}\left(\left|0\right\rangle - i\left|1\right\rangle \right) }[/math] instead of [math]\displaystyle{ \frac{1}{\sqrt{2}}\left(\left|0\right\rangle +\left|1\right\rangle \right) }[/math].

DQC1-complete Problems

In addition to unitary trace estimation, estimating a coefficient in the Pauli decomposition of a unitary and approximating the Jones polynomial at a fifth root of unity are also DQC1-complete. In fact, trace estimation is a special case of Pauli decomposition coefficient estimation.