Parallel multidimensional digital signal processing

Parallel multidimensional digital signal processing (mD-DSP) is defined as the application of parallel programming and multiprocessing to digital signal processing techniques to process digital signals that have more than a single dimension. The use of mD-DSP is fundamental to many application areas such as digital image and video processing, medical imaging, geophysical signal analysis, sonar, radar, lidar, array processing, computer vision, computational photography, and augmented and virtual reality. However, as the number of dimensions of a signal increases the computational complexity to operate on the signal increases rapidly. This relationship between the number of dimensions and the amount of complexity, related to both time and space, as studied in the field of algorithm analysis, is analogues to the concept of the curse of dimensionality. This large complexity generally results in an extremely long execution run-time of a given mD-DSP application rendering its usage to become impractical for many applications; especially for real-time applications. This long run-time is the primary motivation of applying parallel algorithmic techniques to mD-DSP problems.

Motivation, problem statement, and basic concepts

Due to the end of frequency scaling of processors, which is largely attributed to the effect of Dennard scaling around the year 2005, a common trend of processor manufacturers was to continue to exploit Moore's law by increasing the number of processors on a single chip, which are termed multi-core processors as opposed to uniprocessors.

mD-DSP algorithms exhibit a large amount of complexity, as described in the previous section, which makes efficient implementation difficult in regard to run-time and power consumption. This article primarily addresses basic parallel concepts used to alleviate run-time of common mD-DSP applications. The concept of parallel computing can be applied to mD-DSP applications to exploit the fact that if a problem can be expressed in a parallel algorithmic form, then parallel programming and multiprocessing can be used in an attempt to increase the computational throughput of the mD-DSP procedure on a given hardware platform. An increase in computational throughput can result in a decreased run-time, i.e. a speedup of a specific mD-DSP algorithm.

In addition to increasing computational throughput, a generally considered equally important goal is to maximally utilize the memory bandwidth of a given computing memory architecture. The combination of the computational throughput and memory bandwidth usage can be achieved through the concept of operational intensity, which is summarized in what is referred to as the roofline model. The concepts of operational intensity and the roofline model in general have recently become popular methods of quantifying the performance of mD-DSP algorithms.

Increasing throughput can be beneficial to strong scaling of a given mD-DSP algorithm. Another possible benefit of increasing operational intensity is to allow for an increase in weak scaling, which allows the mD-DSP procedure to operate on increased data sizes or larger data sets, which is important for application areas such as data mining and the training of deep neural networks using big data.

The goal of parallizing an algorithm is not always to decrease the traditional concept of complexity of the algorithm because the term complexity as used in this context typically refers to the RAM abstract computer model, which by definition is serial. Parallel abstract computer models such as PRAM have been proposed to describe complexity for parallel algorithms such as mD signal processing algorithms.

Another factor that is important to the performance of mD-DSP algorithm implementations is the resulting energy consumption and power dissipation.

Existing approaches

Parallel implementations of multidimensional discrete fourier transforms

As a simple example of an mD-DSP algorithm that is commonly decomposed into a parallel form, let’s consider the parallelization of the discrete Fourier transform, which is generally implemented using a form of the Fast Fourier Transform (FFT). There are hundreds of available software libraries that offer optimized FFT algorithms, and many of which offer parallelized versions of mD-FFT algorithms with the most popular being the parallel versions of the FFTw library.

The most straightforward method of paralyzing the DFT is to utilize the row-column decomposition method. The following derivation is a close paraphrasing from the classical text Multidimensional Digital Signal Processing. The row-column decomposition can be applied to an arbitrary number of dimensions, but for illustrative purposes, the 2D row-column decomposition of the DFT will be described first. The 2D DFT is defined as

[math]\displaystyle{ X \left( k_1, k_2 \right) = \sum_{n_1=0}^{N_1-1} \sum_{n_2=0}^{N_2-1} x \left( n_1, n_2 \right) W_{N_2}^{n_2 k_2} W_{N_1}^{n_1 k_1} }[/math]

where term [math]\displaystyle{ W_{N} \stackrel{\text{def}}{=}\ \exp \left( -j \frac{2\pi}{N} \right) }[/math] is commonly referred to as the twiddle factor of the DFT in the signal processing literature.

The DFT equation can be re-written in the following form

[math]\displaystyle{ X(k_1, k_2) = \sum_{n_1=0}^{N_1-1} \left[ \sum_{n_2=0}^{N_2-1} \left( x(n_1,n_2) W_{N_2}^{n_2 k_2} \right) \right] W_{N_1}^{n_1 k_1} }[/math]

where the quantity inside the brackets is a 2D sequence which we will denote as [math]\displaystyle{ G \left( n_1, k_2 \right) }[/math]. We can then express the above equation as the pair of relations

[math]\displaystyle{ G(n_1,k_2) = \sum_{n_2=0}^{N_2-1} x(n_1,n_2) W_{N_2}^{n_2 k_2} }[/math]

[math]\displaystyle{ X(k_1,k_2) = \sum_{n_1=0}^{N_1-1} G(n_1,k_2) W_{N_1}^{n_1 k_1} }[/math]

Each column of [math]\displaystyle{ G }[/math] is the 1D DFT of the corresponding column of [math]\displaystyle{ x }[/math]. Each row of [math]\displaystyle{ X }[/math] is the 1D DFT of the corresponding row of [math]\displaystyle{ G }[/math]. Expressing the 2D-DFT in the above form allows us to see that we can compute a 2D DFT by decomposing it into row and column DFTs. The DFT of each column of [math]\displaystyle{ x }[/math] can first be computed where the results of which are placed into an intermediate array. Then we can compute the DFT of each row of the intermediate array.

This row-column decomposition process can easily be extended to compute an mD DFT. First, the 1D DFT is computed with respect to one of the independent variables, say [math]\displaystyle{ n_M }[/math], for each value of the remaining variables. Next, 1D DFTs are computed with respect to the variable [math]\displaystyle{ n_{M-1} }[/math] for all values of the [math]\displaystyle{ ( M-1) }[/math]-tuple [math]\displaystyle{ ( n_1, n_2,\ldots, n_{M-2},k_M) }[/math]. We continue in this fashion until all 1D DFTs have been evaluated with respect to all the spatial variables.

The row-column decomposition of the DFT is parallelized in its most simplistic manner by noting that the row and column computations are independent of each other and therefore can be performed on separate processors in parallel. The parallel 1D DFT computations on each processor can then utilize the FFT algorithm for further optimization. One large advantage of this specific method of parallelizing an mD DFT is that each of the 1D FFTs being performed in parallel on separate processors can then be performed in a concurrent fashion on Shared memory multithreaded SIMD processors .

A specifically convenient hardware platform that has the ability to simultaneous perform both parallel and concurrent DFT implementation techniques that is highly amenable to are GPUs due to common GPUs having both a separate set of multithreaded SIMD processors (which are referred to as "streaming multiprocessors" in the CUDA programming language, and "compute units" in the OpenCL language) and individual SIMD lanes (commonly referred to loosely as a "core", or more specifically a CUDA "thread processor" or as an OpenCL "processing element") within each multithreaded SIMD processor.

A disadvantage to this technique of applying a separate FFT on each shared memory multiprocessor is the required interleaving of the data among the shared memory. One of the most popular libraries that utilizes this basic form of concurrent FFT computation is in the shared memory version of the FFTw library.

Parallel implementations of multidimensional FIR filter structures

The section will describe a method of implementing an mD digital finite impulse response (FIR) filter in a completely parallel realization. The proposed method for a completely parallel realization of a general FIR filter is achieved through the use of a combination of parallel sections consisting of cascaded 1D digital filters.

Consider the general desired ideal finite extent mD FIR digital filter in the complex [math]\displaystyle{ z }[/math]-domain, given as

[math]\displaystyle{ H_d(z_1,z_2,\ldots,z_M) = \sum_{n_1=0}^{N_1} \sum_{n_2=0}^{N_2} \cdots \sum_{n_M=0}^{N_M} a(n_1,n_2,\ldots,n_M) z_1^{-n_1} z_2^{-n_2} \cdots z_3^{-n_M} }[/math]

Placing the coefficients of [math]\displaystyle{ a(n_1,n_2,\ldots,n_M) }[/math] into an array [math]\displaystyle{ C=[c(l_1,l_2,\ldots,l_M)] }[/math] and performing some algebraic manipulation as described in, we are able to arrive at an expression that allows us to decompose the filter into a parallel filterbank, given as

[math]\displaystyle{ H_d(z_1,z_2,\ldots,z_M) \approx H(z_1,z_2,\ldots,z_M) = \sum_{i=1}^{r} E_i(z_1) F_i(z_2) \cdots G_i(z_M) }[/math]

where

[math]\displaystyle{ E_i(z_1) = \sum_{n_1=0}^{N_1}C_{i1}(n_1+1) z_1^{-n_1} }[/math]

[math]\displaystyle{ F_i(z_2) = \sum_{n_2=0}^{N_3}C_{i2}(n_2+1) z_2^{-n_2} }[/math]

[math]\displaystyle{ G_i(z_M) = \sum_{n_M=0}^{N_M}C_{iM}(n_M+1) z_M^{-n_M} }[/math]

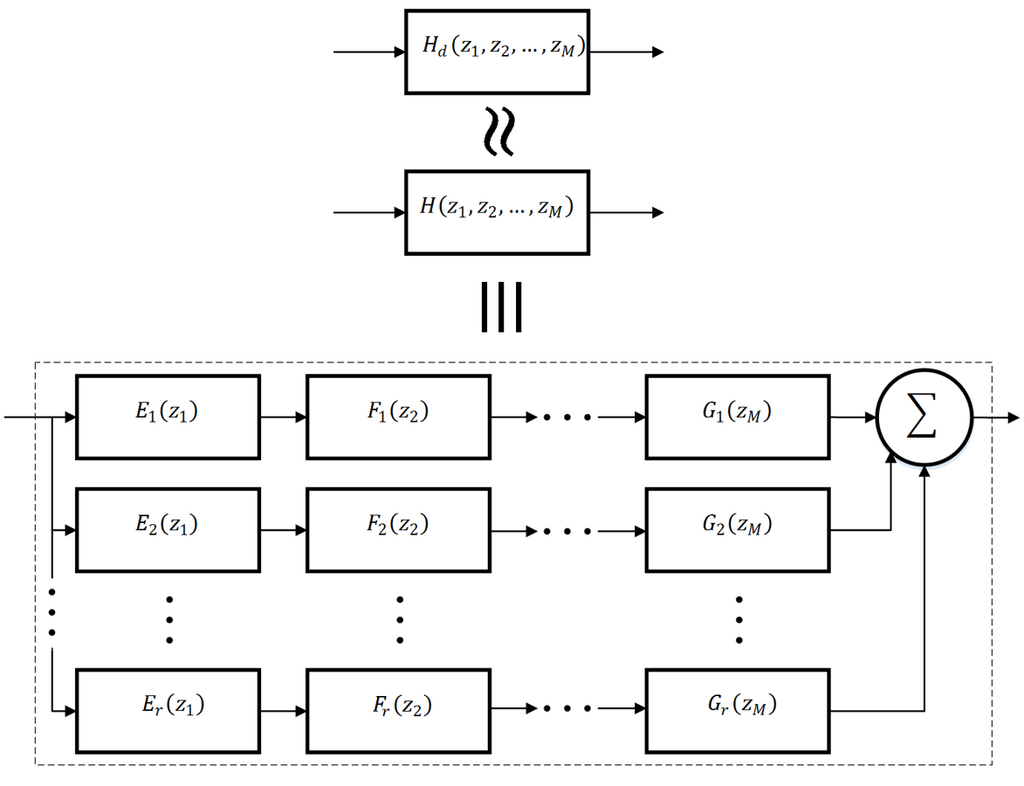
Therefore, the original MD digital filter [math]\displaystyle{ H_d(z_1,z_2,\ldots,z_M) }[/math] is approximately decomposed into a parallel filterbank realization composed of a set of separable parallel filters [math]\displaystyle{ E(z_1), F(z_2), G(z_M) }[/math], such that [math]\displaystyle{ H_d(z_1,z_2,\ldots,z_M) \approx H(z_1,z_2,\ldots,z_M) }[/math]. This proposed parallel FIR filter realization is represented by the block diagram as seen in Figure 1.

Figure 1. A completely parallel realization of an M-Dimensional FIR filter.

The completely parallel realization as seen in figure 1 can be implemented in hardware by noting that block diagrams, and their corresponding Signal-flow graphs (SFGs) are a useful method of graphically representing any DSP algorithm that can be expressed as a linear constant coefficient difference equation. SFGs allow for easy transition from a difference equation into a hardware implementation by allowing one to visualize the difference equation in terms of digital logic components such as shift registers, and basic ALU digital circuit elements such as adders and multipliers. For this specific parallel realization, one could place each parallel section on a separate parallel processor to allow for each section to be implemented in a completely task-parallel fashion.

Using the fork–join parallel programming model, a 'fork' may be applied at the first pickoff point in Figure 1, and the summing junction can be implemented during a synchronization with a 'join' operation. Implementing an mD FIR filter in this fashion lends itself well to the MapReduce general programming model

Implementations of multidimensional discrete convolution via shift registers on an FPGA

Convolution on mD signals lends itself well to pipelining due to the fact each of single output convolution operation is independent of every other one. Due to this data independence between each convolution operation between the filters impulse response and the signal a new set of data calculations may begin at the instant the first convolution operation is finished. A common method of performing mD convolution in a raster scan fashion (including dimensions greater than 2) on a traditional general purpose CPU, or even a GPU, is to cache the set of output data from each scan line of each independent dimension into the local cache. By utilizing the unique custom re-configurable architecture of a field-programmable gate array (FPGA) we can optimize this procedure dramatically by customizing the cache structure.

As in the illustrative example found in the presentation this description is derived from we are going to restrict our discussion to two dimensional signals. In the example we perform a set of convolutional operations between a general 2D signal and a 3x3 filter kernel. As the sequence of convolution operations proceed along each raster line the filter kernel is slid across one dimension of the input signal and the data read from the memory is cached. The first pass loads three new lines of data into cache. The OpenCL code for this procedure is scene below.

// Using a cache to hide poor memory access patterns on a traditional general purpose processor
for (int y = 1; y < yDim-1; ++y) {
  for (int x = 1; x < xDim-1; ++x) {
    // 3x3 Filter Kernel
    for (int y2 = -1; y2 < 1; ++y2) {
      for (int x2 = -1; x2 < 1; ++x2) {
        cache_temp[y][x] += 2D_input_signal[y+y2][x+x2]
                          * kernel[y2][x2];
        //...
      }
    }
  }
}

This caching technique is used to hide poor data to memory access pattern efficiency in terms of coalescing. However, with each successive loop only a single cache-line is updated. If we make the reasonable assumption of a 1 pixel per cycle performance point, applying this proposed caching technique to an FPGA results in a cache requirement of 9 reads and one write per cycle. Utilizing this caching technique on an FPGA results in inefficient performance in terms of both power consumption and a creation of a larger memory footprint than is required because there is a great deal of redundant reads into the cache. With an FPGA we can customize the cache structure to give rise to a much more efficient result.

The proposed method to alleviate this poor performance with an FPGA implementation as proposed in the corresponding literature is to customize the cache architecture through utilization of the re-configurable hardware resources of the FPGA. The important attribute to note here is that the FPGA creates the hardware based on the code that we write as opposed to writing code to run on a fixed architecture with a set of fixed instructions.

A description of how to modify the implementation to optimize the cache architecture on an FPGA will now be discussed. Again, let's begin with an initial 2D signal and assume it is of size [math]\displaystyle{ W \times W }[/math]. We can then remove all of the lines that aren't in the neighborhood of the window. We next can linearize the 2D signal of this restricted segment of the 2D signal after removing lines that aren't in the neighborhood of the window. We can achieve this linearization via a simple row-major data layout. After linearizing the 2D signal into a 1D array, under the assumption that we are not concerned with the boundary conditions of the convolution, we can discard any pixels that only contribute to the boundary computations – which is common in practice for many practical applications. Now, when we slide the window over each array element to perform the next computation, we have effectively created a shift register. The corresponding code for our shift register implementation of achieving this 2D filtering can be seen below.

// Shift register in OpenCL
pixel_t sr[2*W+3];
while (keep_going) {
  // Shift data in
  #pragma unroll
  for (int i=1; i<2*W+3; ++i)
    sr[i] = sr[i-1];
  sr[0] = data_in

  // Tap output data
  data_out = {sr[  0], sr[    1], sr[    2],
              sr[  2], sr[  W+1], sr[  W+2],
              sr[2*W], sr[2*W+1], sr[2*W+2]};
  //...
}

By performing the aforementioned steps, the goal is to manage the data movement to match the FPGAs architectural strengths to achieve the highest performance. These architectural strengths allow custom implementation that can be based on the work being done as opposed to leveraging fixed operations, fixed data paths, and fixed data widths, as would be done on a general purpose processor.