Parametric family

In mathematics and its applications, a parametric family or a parameterized family is a family of objects (a set of related objects) whose differences depend only on the chosen values for a set of parameters.

Common examples are parametrized (families of) functions, probability distributions, curves, shapes, etc.

In probability and its applications

A graph of the probability density functions of several normal distributions (from the same parametric family).

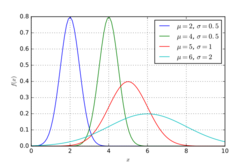
For example, the probability density function f_X of a random variable X may depend on a parameter θ. In that case, the function may be denoted [math]\displaystyle{ f_X( \cdot \, ; \theta) }[/math] to indicate the dependence on the parameter θ. θ is not a formal argument of the function as it is considered to be fixed. However, each different value of the parameter gives a different probability density function. Then the parametric family of densities is the set of functions [math]\displaystyle{ \{ f_X( \cdot \, ; \theta) \mid \theta \in \Theta \} }[/math], where Θ denotes the parameter space, the set of all possible values that the parameter θ can take. As an example, the normal distribution is a family of similarly-shaped distributions parametrized by their mean and their variance.

In decision theory, two-moment decision models can be applied when the decision-maker is faced with random variables drawn from a location-scale family of probability distributions.

In algebra and its applications

A three-dimensional graph of a Cobb–Douglas production function.

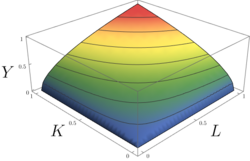
In economics, the Cobb–Douglas production function is a family of production functions parametrized by the elasticities of output with respect to the various factors of production.

Graphs of several quadratic polynomials, varying each of the three coefficients independently.

In algebra, the quadratic equation, for example, is actually a family of equations parametrized by the coefficients of the variable and of its square and by the constant term.

See also

• Indexed family