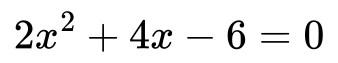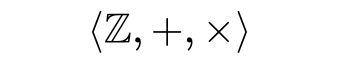Algebra
Algebra is the branch of mathematics that studies algebraic systems and the manipulation of equations within those systems. It is a generalization of arithmetic that includes variables besides regular numbers and algebraic operations other than the standard arithmetic operations like addition and multiplication.
Elementary algebra is the main form of algebra taught in school and examines mathematical statements using variables for unspecified values. It seeks to determine for which values the statements are true. To do so, it utilizes different methods of transforming equations to isolate variables. Linear algebra is a closely related field investigating variables that appear in several linear equations, so-called systems of linear equations. It tries to discover the values that solve all equations at the same time.
Abstract algebra studies algebraic structures, which consist of a set of mathematical objects together with one or several binary operations defined on that set. It is a generalization of elementary and linear algebra since it allows mathematical objects other than numbers and non-arithmetic operations. It distinguishes between different types of algebraic structures, such as groups, rings, and fields, based on the number of operations they use and the laws they follow. Universal algebra constitutes a further level of generalization that is not limited to binary operations and investigates more abstract patterns that characterize algebraic structures.
Algebraic methods were first studied in the ancient period to solve specific problems in fields like geometry. Subsequent mathematicians examined general techniques to solve equations independent of their specific applications. They relied on verbal descriptions of problems and solutions until the 16th and 17th centuries, when a rigorous mathematical formalism was developed. In the mid-19th century, the scope of algebra broadened beyond a theory of equations to cover diverse types of algebraic operations and algebraic structures.
Algebra is relevant to many branches of mathematics, like geometry, topology, number theory, and calculus, and other fields of inquiry, like logic and the empirical sciences.
Definition and etymology
Algebra is the branch of mathematics that studies algebraic operations[lower-alpha 1] and algebraic structures.[2] An algebraic structure is a non-empty set of mathematical objects, such as the real numbers, together algebraic operations defined on that set, such addition and multiplication.[3] Algebra explores the laws, general characteristics, and types of algebraic structures. Within certain algebraic structures, it studies the use of variables in equations and how to manipulate these equations.[4]
Algebra is often understood as a generalization of arithmetic.[5] Arithmetic studies arithmetic operations, like addition, subtraction, multiplication, and division, in a specific domain of numbers, like the real numbers.[6] Elementary algebra constitutes the first level of abstraction. Like arithmetic, it restricts itself to specific types of numbers and operations. It generalizes these operations by allowing indefinite quantities in the form of variables in addition to numbers.[7] A higher level of abstraction is achieved in abstract algebra, which is not limited to a specific domain and studies different classes of algebraic structures, like groups and rings. These algebraic structures are not restricted to typical arithmetic operations and cover other binary operations besides them.[8] Universal algebra is still more abstract in that it is not limited to binary operations and not interested in specific classes of algebraic structures but investigates the characteristics of algebraic structures in general.[9]

The term "algebra" is sometimes used in a more narrow sense to refer only to elementary algebra or only to abstract algebra.[11] When used as a countable noun, an algebra is a specific type of algebraic structure that involves a vector space equipped with a certain type of binary operation.[12] Depending on the context, "algebra" can also refer to other algebraic structures, like a Lie algebra or an associative algebra.[13]
The word algebra comes from the Arabic term الجبر (al-jabr) and originally referred to the surgical treatment of bonesetting. In the 9th century, the term received a mathematical meaning in the work The Compendious Book on Calculation by Completion and Balancing, in which the Persian mathematician Muhammad ibn Musa al-Khwarizmi used it to describe a method of solving equations. The word entered the English language in the 16th century from Italian, Spanish, and medieval Latin.[14] Initially, the meaning of the term was restricted to the theory of equations, that is, to the art of manipulating polynomial equations in view of solving them. This changed in the course of the 19th century[lower-alpha 2] when the scope of algebra broadened to cover the study of diverse types of algebraic operations and algebraic structures together with their underlying axioms.[17]
Major branches
Elementary algebra
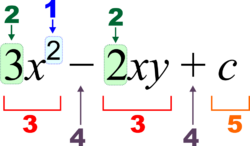
1 – power (exponent)
2 – coefficient
3 – term
4 – operator
5 – constant term
x y c – variables/constants
Elementary algebra, also referred to as school algebra, college algebra, and classical algebra,[18] is the oldest and most basic form of algebra. It is a generalization of arithmetic that relies on the use of variables and examines how formulas may be transformed.[19]
Arithmetic is the study of numerical operations and investigates how numbers are combined and transformed using arithmetic operations like addition, subtraction, multiplication, and division. For example, the operation of addition combines two numbers, called the addends, into a third number, called the sum, as in .[6]
Elementary algebra relies on the same operations while allowing variables in addition to regular numbers. Variables are symbols for unspecified or unknown quantities. They make it possible to state relationships for which one does not know the exact values and to express general laws that are true independent of which numbers are used. For example, the equation belongs to arithmetic and expresses an equality only for these specific numbers. By replacing the numbers with variables, it is possible to express a general law that applies to any possible combinations of numbers, as in the equation .[19]
Elementary algebra is interested in algebraic expressions, which are formed by using arithmetic operations to combine variables and numbers. For example, the expression is an algebraic expression created by multiplying the number 5 with the variable x and adding the number 3 to the result. Other examples of algebraic equations are and .[20]
Algebraic expressions are used to construct statements that relate two expressions to one another. An equation is a statement formed by comparing two expressions with an equals sign (=), as in . Inequations are formed with symbols like the less-than sign (<) and the greater-than sign (>). Unlike mere expressions, statements can be true or false and their truth value usually depends on the values of the variables. For example, the statement is true if x is either 2 or -2 and false otherwise.[21]
The main objective of elementary algebra is to determine for which values a statement is true. To achieve this, it relies on different techniques used to transform and manipulate statements. A key principle guiding this process is that whatever is done to one side of an equation also needs to be done to the other side of the equation. For example, if one subtracts 5 from the left side of an equation one also needs to subtract 5 from the right side of the equation to balance both sides. The goal of these steps is usually to isolate the variable one is interested in on one side, a process known as solving the equation for that variable. For example, the equation can be solved for x by adding 7 to both sides, which isolates x on the left side and results in the equation .[22]
There are many other techniques used to solve equations. Simplification is employed to replace a complicated expression with an equivalent simpler one. For example, the expression can be replaced with the expression .[23] Factorization is used to rewrite an expression as a product of several factors. This technique is common for polynomials to determine for which values the expression is zero. For example, the polynomial can be factorized as . The polynomial as a whole is zero if one of its factors is zero, i.e., if x is either -2 or 5.[24] For statements with several variables, substitution is a common technique to replace one variable with an equivalent expression that does not use this variable. For example, if one knows that then one can simplify the expression to arrive at .[25] Other techniques rely on commutative, distributive, and associative properties.[26]
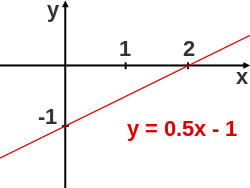
Elementary algebra has applications in many branches of mathematics, the sciences, business, and everyday life.[27] An important application in the field of geometry concerns the use of algebraic equations to describe geometric figures in the form of a graph. To do so, the different variables in the equation are interpreted as coordinates and the values that solve the equation are interpreted as points of the graph. For example, if x is set to zero in the equation then y has to be −1 for the equation to be true. This means that the x-y-pair (0, −1) is part of the graph of the equation. The x-y-pair (0, 7), by contrast, does not solve the equation and is therefore not part of the graph. The graph encompasses the totality of all x-y-pairs that solve the equation.[28]
Linear algebra
Linear algebra employs the methods of elementary algebra to study systems of linear equations.[29] An equation is linear if no variable is multiplied with another variable and no operations like exponentiation, extraction of roots, and logarithm are applied to variables. For example, the equations and are linear while the equations and are non-linear. Several equations form a system of equations if they all rely on the same set of variables.[30]
Systems of linear equations are often expressed through matrices[lower-alpha 3] and vectors[lower-alpha 4] to represent the whole system in a single equation. This can be done by moving the variables to the left side of each equation and moving the constant terms to the right side. The system is then expressed by formulating a matrix that contains all the coefficients of the equations and multiplying it with the vector made up of the variables.[31] For example, the system of equations
can be written as
Like elementary algebra, linear algebra is interested in manipulating and transforming equations to solve them. It goes beyond elementary algebra by dealing with several equations at once and looking for the values for which all equations are true at the same time. For example, if the system is made of the two equations and then using the values 1 and 3 for and does not solve the system of equations because it only solves the first but not the second equation.[32]
Two central questions in linear algebra are whether a system of equations has any solutions and, if so, whether it has a unique solution. A system of equations that has solutions is called consistent. This is the case if the equations do not contradict each other. If two or more equations contradict each other, the system of equations is inconsistent and has no solutions. For example, the equations and contradict each other since no values of and exist that solve both equations at the same time.[33]
Whether a consistent system of equations has a unique solution depends on the number of variables and the number of independent equations. Several equations are independent of each other if they do not provide the same information and cannot be derived from each other. A unique solution exists if the number of variables is the same as the number of independent equations. Underdetermined systems, by contrast, have more variables than equations and have an infinite number of solutions if they are consistent.[34]
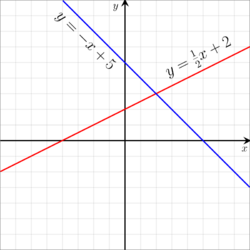
Many of the techniques employed in elementary algebra to solve equations are also applied in linear algebra. The substitution method starts with one equation and isolates one variable in it. It proceeds to the next equation and replaces the isolated variable with the found expression, thereby reducing the number of unknown variables by one. It applies the same process again to this and the remaining equations until the values of all variables are determined.[35] The elimination method creates a new equation by adding one equation to another equation. This way, it is possible to eliminate one variable that appears in both equations. For a system that contains the equations and , it is possible to eliminate y by adding the first to the second equation, thereby revealing that x is 13.[lower-alpha 5][36] Many advanced techniques implement algorithms based on matrix calculations, such as Cramer's rule, the Gauss–Jordan elimination, and LU Decomposition.[37]
On a geometric level, systems of equations can be interpreted as geometric figures. For systems that have two variables, each equation represents a line in two-dimensional space. The point where the two lines intersect is the solution. For inconsistent systems, the two lines run parallel, meaning that there is no solution since they never intersect. If two equations are not independent then they describe the same line, meaning that every solution of one equation is also a solution of the other equation. These relations make it possible to graphically look for solutions by plotting the equations and determining where they intersect.[38] The same principles also apply to systems of equations with more variables, with the difference being that the equations do not describe lines but higher dimensional figures. For instance, equations with three variables correspond to planes in three-dimensional space and the points where all planes intersect solve the system of equations.[39]
Abstract algebra
Abstract algebra, also called modern algebra,[40] studies different types of algebraic structures. An algebraic structure is a framework for understanding operations on mathematical objects, like the addition of numbers. While elementary algebra and linear algebra work within the confines of particular algebraic structures, abstract algebra takes a more general approach that compares how algebraic structures differ from each other and what types of algebraic structures there are, such as groups, rings, and fields.[41]

On a formal level, an algebraic structure is a set[lower-alpha 6] of mathematical objects, called the underlying set, together with one or several operations.[lower-alpha 7] Abstract algebra usually restricts itself to binary operations that take any two objects from the underlying set as inputs and map them to another object from this set as output.[44] For example, the algebraic structure has the natural numbers as the underlying set. Addition is its binary operation and takes two numbers as input to produce one number in the form of the sum as output.[43] The underlying set can contain mathematical objects other than numbers and the operations are not restricted to regular arithmetic operations.[45]
Abstract algebra classifies algebraic structures based on the laws or axioms that its operations obey and the number of operations it uses. One of the most basic types is a group, which has one operation and requires that this operation is associative and has an identity element and inverse elements. An operation[lower-alpha 8] is associative if the order of several applications does not matter, i.e., if is the same as for all elements. An operation has an identity element or a neutral element if one element e exists that does not change the value of any other element, i.e., if . An operation admits inverse elements if for any element there exists a reciprocal element that reverses its effects. If an element is linked to its inverse then the result is the neutral element e, expressed formally as . Every algebraic structure that fulfills these requirements is a group.[46] For example, is a group formed by the set of integers together with the operation of addition. The neutral element is 0 and the inverse element of any number is .[47] The natural numbers, by contrast, do not form a group since they contain only positive numbers and therefore lack inverse elements.[48] Group theory is the subdiscipline of abstract algebra studying groups.[49]
A ring is an algebraic structure with two operations ( and ) that work similarly to addition and multiplication. All the requirements of groups also apply to the first operation: it is associative and has an identity element and inverse elements. Additionally, it is commutative, meaning that is true for all elements. The axiom of distributivity governs how the two operations interact with each other. It states that and .[lower-alpha 9][51] The ring of integers is a ring of the form .[52] A ring becomes a field if both operations follow the axioms of associativity, commutativity, and distributivity and if both operations have an identity element and inverse elements.[lower-alpha 10][54] The ring of integers does not form a field because it lacks multiplicative inverses. For example, the multiplicative inverse of is , which is not part of the integers. The rational numbers, the real numbers, and the complex numbers each form a field.[55]
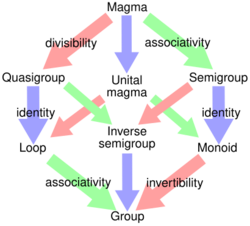
Besides groups, rings, and fields, there are many other algebraic structures studied by abstract algebra. They include magmas, semigroups, monoids, abelian groups, commutative rings, modules, lattices, vector spaces, and algebras over a field. They differ from each other in regard to the types of objects they describe and the requirements that their operations fulfill. Many of them are related to each other in that a basic structure can be turned into a more advanced structure by adding additional requirements.[56] For example, a magma becomes a semigroup if its operation is associative.[57]
Universal algebra
Universal algebra is the study of algebraic structures in general. It is a generalization of abstract algebra that is not limited to binary operations and allows operations with more inputs as well, such as ternary operations. Universal algebra is not interested in the specific elements that make up the underlying sets and instead investigates what structural features different algebraic structures have in common.[58] One of those structural features concerns the identities that are true in different algebraic structures. In this context, an identity is a universal equation or an equation that is true for all elements of the underlying set. For example, commutativity is a universal equation that states that is identical to for all elements.[59] Two algebraic structures that share all their identities are said to belong to the same variety.[60] For instance, the ring of integers and the ring of polynomials form part of the same variety because they have the same identities, such as commutativity and associativity. The field of rational numbers, by contrast, does not belong to this variety since it has additional identities, such as the existence of multiplicative inverses.[61]
Besides identities, universal algebra is also interested in structural features associated with quasi-identities. A quasi-identity is an identity that only needs to be present under certain conditions.[lower-alpha 11] It is a generalization of identity in the sense that every identity is a quasi-identity but not every quasi-identity is an identity. Algebraic structures that share all their quasi-identities have certain structural characteristics in common, which is expressed by stating that they belong to the same quasivariety.[62]
Homomorphisms are a tool in universal algebra to examine structural features by comparing two algebraic structures.[63] A homomorphism is a function that takes the elements of the underlying set of one algebraic structure as input and has the elements of the underlying set of another algebraic structure as output. Its special feature is that it preserves certain structural characteristics of the algebraic structures. If the two algebraic structures use binary operations and have the form and then the function is a homomorphism if it fulfills the following requirement: . The existence of a homomorphism reveals that the operation in the second algebraic structure plays the same role as the operation does in the first algebraic structure.[64]
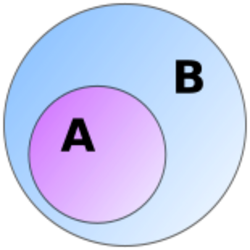
Another tool of comparison is the relation between an algebraic structure and its subalgebra.[65] If is a subalgebra of then the set A is a subset of B.[lower-alpha 12] A subalgebra has to use the same operations as the algebraic structure[lower-alpha 13] and they have to follow the same axioms. This includes the requirement that all operations in the subalgebra are closed in A, meaning that they only produce elements that belong to A.[65] For example, the set of even integers together with addition is a subalgebra of the full set of integers together with addition. This is the case because the sum of two even numbers is again an even number. But the set of odd integers together with addition is not a subalgebra since adding two odd numbers produces an even number, which is not part of the chosen subset.[66]
History

The origin of algebra lies in attempts to solve mathematical problems involving arithmetic calculations, usually in the form of a theory of equations. These developments happend in the ancient period in diverse regions such as Babylonia, Egypt, Ancient Greece , China, and India. One of the earliest documents is the Rhind Papyrus from ancient Egypt, which was written around 1650 BCE[lower-alpha 14] and discusses how to solve linear equations, as expressed in problems like "A quantity; its fourth is added to it. It becomes fifteen. What is the quantity?" Babylonian clay tablets from around the same time explain methods to solve linear and quadratic polynomial equations, such as the method of completing the square.[67]
Many of these insights found their way to the ancient Greeks. Starting in the 6th century BCE, their main interest was geometry rather than algebra, but they employed algebraic methods to solve geometric problems. For example, they studied geometric figures while taking their lengths and areas as unknown quantities to be determined, as exemplified in Pythagoras' formulation of the difference of two squares method and later in Euclid's Elements.[68] In the 3rd century BCE, Diophantus provided a detailed treatment of how to solve algebraic equations in a series of books called Arithmetica. He was the first to experiment with symbolic notation to express polynomials.[69] In ancient China, the book The Nine Chapters on the Mathematical Art explored various techniques for solving algebraic equations, including the use of matrix-like constructs.[70]

It is controversial to what extent these early developments should be considered part of algebra proper rather than precursors. They offered solutions to algebraic problems but did not conceive them in an abstract and general manner, focusing instead on specific cases and applications.[71] This changed with the Persian mathematician al-Khwarizmi,[lower-alpha 15] who published his The Compendious Book on Calculation by Completion and Balancing in 825 CE. It presents the first detailed treatment of general methods that can be used to manipulate linear and quadratic equations by "reducing" and "balancing" both sides.[73] Other influential contributions to algebra came from the Arab mathematician Thābit ibn Qurra in the 9th century and the Persian mathematician Omar Khayyam in the 11th and 12th centuries.[74]
In India, Brahmagupta investigated how to solve quadratic equations and systems of equations with several variables in the 7th century CE. Among his other innovations were the use of zero and negative numbers in algebraic equations.[75] The Indian mathematicians Mahāvīra in the 9th century and Bhāskara II in the 12th century further refined Brahmagupta's methods and concepts.[76] In 1247, the Chinese mathematician Qin Jiushao wrote the Mathematical Treatise in Nine Sections, which includes an algorithm for the numerical evaluation of polynomials, including polynomials of higher degrees.[77]
The Italian mathematician Fibonacci brought al-Khwarizmi's ideas and techniques to Europe in books like his Liber Abaci.[78] In 1545, the Italian polymath Gerolamo Cardano published his book Ars Magna, which covered many topics in algebra and was the first to present general methods for solving cubic and quartic equations.[79] In the 16th and 17th centuries, the French mathematicians François Viète and René Descartes introduced letters and symbols to denote variables and operations, making it possible to express equations as mathematical formulas. Their predecessors had relied on verbal descriptions of problems and solutions.[80] Some historians see this development as a key turning point in the history of algebra and consider what came before it as the prehistory of algebra because it lacked the abstract nature based on symbolic manipulation.[81]

Many attempts in the 17th and 18th centuries to find general solutions[lower-alpha 16] to polynomials of degree five and higher failed.[84] At the end of the 18th century, the German mathematician Carl Friedrich Gauss proved the fundamental theorem of algebra, which describes the existence of zeros of polynomials of any degree without providing a general solution.[15] At the beginning of the 19th century, the Italian mathematician Paolo Ruffini and the Norwegian mathematician Niels Henrik Abel were able to show that no general solution exists for polynomials of degree five and higher.[84] In response to and shortly after their findings, the French mathematician Évariste Galois developed what came later to be known as Galois theory, which offered a more in-depth analysis of the solutions of polynomials while also laying the foundation of group theory.[16] Mathematicians soon realized the relevance of group theory to other fields and applied it to disciplines like geometry and number theory.[85]
Starting in the mid-19th century, interest in algebra shifted from the study of polynomials associated with elementary algebra towards a more general inquiry into algebraic structures, marking the emergence of abstract algebra. This approach explored the axiomatic basis of arbitrary algebraic operations.[86] The invention of new algebraic systems based on different operations and elements accompanied this development, such as Boolean algebra, vector algebra, and matrix algebra.[87] Influential early developments in abstract algebra were made by the German mathematicians David Hilbert, Ernst Steinitz, Emmy Noether, and Emil Artin. They researched different forms of algebraic structures and categorized them based on their underlying axioms into types, such as groups, rings, and fields.[88] The basic idea of the even more general approach associated with universal algebra was first conceived by the English mathematician Alfred North Whitehead in his 1898 book A Treatise on Universal Algebra. Starting in the 1930s, the American mathematician Garrett Birkhoff expanded these ideas and developed many of the foundational concepts of this field.[89] Closely related developments were the formulation of model theory, category theory, topological algebra, homological algebra, Lie algebras, free algebras, and homology groups.[90]
In various fields
Other branches of mathematics
The algebraization of mathematics is the process of applying algebraic methods and principles to other branches of mathematics. This involves the use of symbols in the form of variables to express mathematical insights on a more general level. Another key aspect is to apply structures to model how different types of objects interact without the need to specify what the nature of these objects is besides their patterns of interaction.[91] This is possible because the abstract patterns studied by algebra have many concrete applications in fields like geometry, topology, number theory, and calculus.[92]
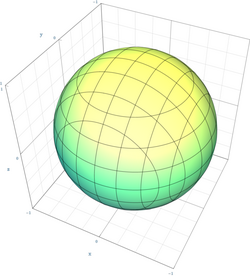
Geometry is interested in geometric figures, which can be described with algebraic statements. For example, the equation describes a line in two-dimensional space while the equation corresponds to a sphere in three-dimensional space. Of special interest to algebraic geometry are algebraic varieties,[lower-alpha 17] which are solutions to systems of polynomial equations that can be used to describe more complex geometric figures.[93] Topology studies the properties of geometric figures or topological spaces that are preserved under operations of continuous deformation. Algebraic topology relies on algebraic theories like group theory to classify topological spaces. For example, homotopy groups classify topological spaces based on the existence of loops or holes in them.[94] Number theory is concerned with the properties of and relations between integers. Algebraic number theory applies algebraic methods to this field of inquiry, for example, by using algebraic expressions to describe laws, such as Fermat's Last Theorem, and by analyzing how numbers form algebraic structures, such as the ring of integers.[95] The insights of algebra are also relevant to calculus, which utilizes mathematical expressions to examine rates of change and accumulation. It relies on algebra to understand how these expressions can be transformed and what role variables play in them.[96] Because of its presence throughout mathematics, the influence of algebra extends to many sciences and related fields, including physics, computer science, and engineering.[97]
Logic
Logic is the study of correct reasoning.[98] Algebraic logic employs algebraic methods to describe and analyze the structures and patterns that underlie logical reasoning.[99] One part of it is interested in understanding the mathematical structures themselves without regard for the concrete consequences they have on the activity of drawing inferences. Another part investigates how the problems of logic can be expressed in the language of algebra and how the insights obtained through algebraic analysis affect logic.[100]
Boolean algebra is an influential device in algebraic logic to describe propositional logic.[101] Propositions are statements that can be true or false.[102] Propositional logic uses logical connectives to combine two propositions to form a complex proposition. For example, the connective "if...then" can be used to combine the propositions "it rains" and "the streets are wet" to form the complex proposition "if it rains then the streets are wet". Propositional logic is interested in how the truth value of a complex proposition depends on the truth values of its constituents.[103] With Boolean algebra, this problem can be addressed by interpreting truth values as numbers: 0 corresponds to false and 1 corresponds to true. Logical connectives are understood as binary operations that take two numbers as input and return the output that corresponds to the truth value of the complex proposition.[104] Algebraic logic is also interested in how more complex systems of logic can be described through algebraic structures and which varieties and quasivarities these algebraic structures belong to.[105]
Education

Algebra education mostly focuses on elementary algebra, which is one of the reasons why it is referred to as school algebra. It is usually introduced in secondary education after students have mastered the fundamentals of arithmetic.[107] It aims to familiarize students with the abstract side of mathematics by helping them understand mathematical symbolism, for example, how variables can be used to represent unknown quantities. An additional difficulty for students lies in the fact that, unlike arithmetic calculations, algebraic expressions often cannot be directly solved. Instead, students need to learn how to transform them according to certain laws until the unknown quantity can be determined.[108]
A common example to introduce students to the basic problems of algebra is to use balance scales to represent equations. The mass of some weights on the scale is unknown and represents variables. Solving an equation corresponds to adding and removing weights on both sides in such a way that the sides stay in balance until the only weight remaining on one side is the weight of unknown mass.[106] The use of word problems is another tool to show how algebra is applied to real-life situations. For example, students may be presented with a situation in which Naomi has twice as many apples as her brother. Given that both together have twelve apples, students are then asked to find an algebraic equation that describes this situation and to determine how many apples Naomi has.[109]
See also
- Algebra over a set
- Algebra tile
- Algebraic combinatorics
- C*-algebra
- Composition algebra
- Computer algebra
- Exterior algebra
- F-algebra
- F-coalgebra
- Heyting algebra
- Hopf algebra
- Non-associative algebra
- Outline of algebra
- Relational algebra
- Sigma-algebra
- Symmetric algebra
- T-algebra
- Tensor algebra
References
Notes
- ↑ When understood in the widest sense, an algebraic operation is mapping from a Cartesian power of a set into that set, expressed formally as . Addition of real numbers is an example of an algebraic operations: it takes two numbers as input and produces one number as output. It has the form .[1]
- ↑ These changes were in part triggered by discoveries that solved many of the older problems of algebra. For example, the proof of the fundamental theorem of algebra demonstrated the existence of complex solutions of polynomials[15] and the introduction of Galois theory characterized the polynomials that have general solutions.[16]
- ↑ A matrix is a table of numbers, such as
- ↑ A vector is an array of numbers or a matrix with only one column, such as
- ↑ In some cases, an equation has to be multiplied by a constant before adding it to another equation.
- ↑ A set is a collection of elements, such as numbers, vectors, or other sets. Set theory describes the laws and properties of sets.[42]
- ↑ According to some definitions, algebraic structures include a distinguished element as an additional component, such as the identity element in the case of multiplication.[43]
- ↑ Symbols like and are often used in abstract algebra to represent any operation that may or may not resemble arithmetic operations.
- ↑ Some definitions additionally require that the second operation is associative.[50]
- ↑ For the second operation, there is usually one element, corresponding to 0, that does not require an inverse element.[53]
- ↑ The conditions take the form of a Horn clause.
- ↑ This means that all the elements of A are also elements of B but B may contain elements that are not found in A.
- ↑ According to some definitions, it is also possible for a subalgebra to have fewer operations.[66]
- ↑ The exact date is disputed.
- ↑ Some historians consider him the "father of algebra" while others reserve this title for Diophantus.[72]
- ↑ A general solution or a solution in radicals is a closed form algebraic equation that isolates the variable on one side. For example, the general solution to quadratic equations of the form is . The absence of general solutions does not mean that there are no numerical solutions.[82][83]
- ↑ Algebraic varieties studied in geometry are different from the more general varieties studied in universal algebra.
Citations
- ↑ EoM Staff 2023, Lead Section
- ↑
- EoM Staff 2020, Lead Section
- Gilbert & Nicholson 2004, p. 4
- ↑
- Fiche & Hebuterne 2013, p. 326
- EoM Staff 2020, § The Subject Matter of Algebra, Its Principal Branches and Its Connection with Other Branches of Mathematics.
- Gilbert & Nicholson 2004, p. 4
- ↑
- Pratt 2022, Lead Section, § 1. Elementary Algebra, § 2. Abstract Algebra, § 3. Universal Algebra
- EoM Staff 2020, § The Subject Matter of Algebra, Its Principal Branches and Its Connection with Other Branches of Mathematics.
- ↑
- Maddocks 2008, p. 129
- Burgin 2022, p. 45
- ↑ 6.0 6.1
- ↑
- Maddocks 2008, pp. 129–130
- Pratt 2022, Lead Section, § 1. Elementary Algebra
- Wagner & Kieran 2018, p. 225
- ↑
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead Section, § 2. Abstract Algebra
- Wagner & Kieran 2018, p. 225
- ↑
- Pratt 2022, § 3. Universal Algebra
- Grillet 2007, p. 559
- ↑
- Cresswell 2010, p. 11
- OUP Staff
- Menini & Oystaeyen 2017, p. 722
- ↑
- ↑
- Weisstein 2003, p. 46
- Renze & Weisstein
- Golan 1995, pp. 219–227
- ↑ EoM Staff 2017
- ↑
- Cresswell 2010, p. 11
- OUP Staff
- Menini & Oystaeyen 2017, p. 722
- Hoad 1993, p. 10
- ↑ 15.0 15.1
- Tanton 2005, p. 10
- Kvasz 2006, p. 308
- Corry 2024, § The Fundamental Theorem of Algebra
- ↑ 16.0 16.1
- Kvasz 2006, pp. 314–345
- EoM Staff 2020, § Historical Survey
- Corry 2024, § Galois Theory, § Applications of Group Theory
- ↑
- Tanton 2005, p. 10
- Corry 2024, § Structural Algebra
- Hazewinkel 1994, pp. 73–74
- ↑
- ↑ 19.0 19.1
- Maddocks 2008, p. 129
- Berggren 2015, Lead Section
- Pratt 2022, § 1. Elementary Algebra
- EoM Staff 2020, § 1. Historical Survey
- ↑
- Maddocks 2008, pp. 129–130
- Young 2010, p. 999
- Majewski 2004, p. 347
- Buthusiem & Toth 2020, pp. 24–28
- Pratt 2022, § 1. Elementary Algebra
- ↑
- Maddocks 2008, pp. 129–130
- Buthusiem & Toth 2020, pp. 24–28
- ↑
- Maddocks 2008, p. 130
- Buthusiem & Toth 2020, pp. 25–28
- Pratt 2022, § 1. Elementary Algebra
- EoM Staff 2020, § 1. Historical Survey
- ↑
- ↑
- Buthusiem & Toth 2020, pp. 24–28
- Berggren 2015, § Algebraic Expressions, § Solving Algebraic Equations
- ↑
- Zill & Dewar 2011, p. 529
- Berggren 2015, § Solving Systems of Algebraic Equations
- McKeague 2014, p. 386
- ↑
- Axler 2011, pp. 7–11
- Berggren 2015, § Algebraic Expressions, § Solving Algebraic Equations
- ↑
- Maddocks 2008, pp. 130–131
- Walz 2016, Algebra
- ↑
- Maddocks 2008, pp. 130–131
- Rohde et al. 2012, p. 89
- Walz 2016, Algebra
- ↑
- Maddocks 2008, p. 131
- Barrera-Mora 2023, pp. ix, 1–2,
- ↑
- Anton & Rorres 2013, pp. 2–3
- Maddocks 2008, p. 131
- EoM Staff 2011
- ↑
- Barrera-Mora 2023, pp. ix, 1, 12–13
- Young 2010, pp. 726–727
- Anton & Rorres 2013, pp. 32–34
- ↑
- Maddocks 2008, p. 131
- Andrilli & Hecker 2022, pp. 57–58
- ↑
- Anton & Rorres 2013, pp. 3–7
- Mortensen 2013, pp. 73–74
- Williams 2007, pp. 4–5
- Young 2023, pp. 714–715
- ↑
- Maddocks 2008, p. 131
- Harrison & Waldron 2011, p. 464
- Anton 2013, p. 255
- ↑
- Young 2010, pp. 697–698
- Maddocks 2008, p. 131
- Sullivan 2010, pp. 53–54
- ↑
- Anton & Rorres 2013, pp. 7–8
- Sullivan 2010, pp. 55–56
- ↑
- Maddocks 2008, p. 131
- Anton & Rorres 2013, pp. 7–8, 11, 491
- ↑
- Anton & Rorres 2013, pp. 3–5
- Young 2010, pp. 696–697
- Williams 2007, pp. 4–5
- ↑
- Anton & Rorres 2013, pp. 3–5
- Young 2010, p. 713
- Williams 2007, pp. 4–5
- ↑
- Gilbert & Nicholson 2004, p. 1
- Dominich 2008, p. 19
- ↑
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead Section, § 2. Abstract Algebra
- Gilbert & Nicholson 2004, pp. 1–3
- Dominich 2008, p. 19
- ↑ Tanton 2005, p. 460
- ↑ 43.0 43.1 Ovchinnikov 2015, p. 27
- ↑
- Ovchinnikov 2015, p. 27
- Fiche & Hebuterne 2013, p. 326
- Gilbert & Nicholson 2004, p. 4
- Pratt 2022, Lead Section, § 2. Abstract Algebra
- ↑
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead Section, § 2. Abstract Algebra
- ↑
- Rowland & Weisstein
- EoM Staff 2016, § Definition
- Khattar & Agrawal 2023, pp. 4–6
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead Section, § 2. Abstract Algebra
- ↑
- Khattar & Agrawal 2023, pp. 6–7
- Maddocks 2008, pp. 131–132
- ↑
- McWeeny 2002, p. 6
- Kramer & Pippich 2017, p. 49
- ↑ Tanton 2005, p. 242
- ↑ Weisstein 2024c
- ↑
- Weisstein 2024c
- EoM Staff 2016a
- Maxwell 2009, pp. 73–74
- Pratt 2022, § 2.3 Rings
- ↑ Terr & Weisstein
- ↑ Weisstein 2024b
- ↑
- Weisstein 2024a
- Weisstein 2024b
- Pratt 2022, § 2.4 Fields
- ↑
- Weisstein 2024a
- Irving 2004, p. 236
- Negro 2022, p. 365
- ↑
- Pratt 2022, Lead Section, § 2. Abstract Algebra
- EoM Staff 2020, The Subject Matter of Algebra, Its Principal Branches and Its Connection with Other Branches of Mathematics.
- ↑ Cooper 2011, p. 60
- ↑
- Pratt 2022, § 3. Universal Algebra
- Insall & Sakharov
- ↑
- Pratt 2022, § 3.2 Equational Logic
- Mal’cev 1973, pp. 210–211
- Insall & Sakharov
- ↑
- Pratt 2022, § 3. Universal Algebra
- Mal’cev 1973, pp. 210–211
- ↑
- ↑
- Mal’cev 1973, pp. 210–211
- Pratt 2022, § 3. Universal Algebra
- Artamonov 2003, p. 873
- ↑
- Insall & Sakharov
- Pratt 2022, § 3.3 Birkhoff’s Theorem
- Grätzer 2008, p. 34
- ↑
- Pratt 2022, § 3.3 Birkhoff’s Theorem
- Insall & Sakharov
- Silvia & Robinson 1979, p. 82
- ↑ 65.0 65.1
- Indurkhya 2013, pp. 217–218
- Pratt 2022, § 3.3 Birkhoff’s Theorem
- Grätzer 2008, p. 34
- ↑ 66.0 66.1 Indurkhya 2013, pp. 217–218
- ↑
- Tanton 2005, p. 9
- Kvasz 2006, p. 290
- Corry 2024, § Problem Solving in Egypt and Babylon
- ↑
- Tanton 2005, p. 9
- Kvasz 2006, p. 290
- Corry 2024, § The Pythagoreans and Euclid
- ↑
- EoM Staff 2020, § Historical Survey
- Sialaros 2018, p. 55
- Musielak 2020, p. 36
- Corry 2024, § Diophantus
- ↑ Higgins 2015, p. 89
- ↑
- Kvasz 2006, pp. 290–291
- Sialaros 2018, p. 55
- Boyer & Merzbach 2011, p. 161
- Derbyshire 2006, p. 31
- ↑
- ↑
- Tanton 2005, p. 10
- Kvasz 2006, pp. 291–293
- EoM Staff 2020, § Historical Survey
- ↑
- Waerden 2013, pp. 3, 15–16, 24–25
- Jr 2010, p. 82
- Pickover 2009, p. 90
- ↑
- Tanton 2005, pp. 9–10
- Corry 2024, § The Equation in India and China
- ↑
- ↑
- Smorynski 2007, p. 137
- Zwillinger 2002, p. 812
- ↑
- Waerden 2013, pp. 32–35
- Tanton 2005, p. 10
- Kvasz 2006, p. 293
- ↑
- Tanton 2005, p. 10
- Kvasz 2006, p. 293
- Corry 2024, § Cardano and the Solving of Cubic and Quartic Equations
- ↑
- Tanton 2005, p. 10
- Kvasz 2006, pp. 291–292, 297–298, 302
- EoM Staff 2020, § Historical Survey
- Corry 2024, § Viète and the Formal Equation, § Analytic Geometry
- ↑
- Hazewinkel 1994, p. 73
- EoM Staff 2020, § Historical Survey
- ↑ Igarashi et al. 2014, p. 103.
- ↑ Sun & Zhang 2020, p. 94.
- ↑ 84.0 84.1
- Tanton 2005, p. 10
- EoM Staff 2020, § Historical Survey
- Corry 2024, § Impasse with Radical Methods
- ↑ Corry 2024, § Applications of Group Theory
- ↑
- EoM Staff 2020, § Historical Survey
- Tanton 2005, p. 10
- Corry 2024, § Structural Algebra
- Hazewinkel 1994, pp. 73–74
- ↑
- EoM Staff 2020, § Historical Survey
- Tanton 2005, p. 10
- Corry 2024, § Matrices, § Quaternions and Vectors
- ↑
- EoM Staff 2020, § Historical Survey
- Corry 2024, § Hilbert and Steinitz, § Noether and Artin
- Hazewinkel 1994, pp. 73–74
- ↑
- Grätzer 2008, p. vii
- Chang & Keisler 1990, p. 603
- Knoebel 2011, p. 5
- Hazewinkel 1994, pp. 74–75
- ↑
- Hazewinkel 1994, pp. 74–75
- Grätzer 2008, p. 338
- Pratt 2022, § 6. Free Algebras
- ↑
- Mancosu 1999, pp. 84–85
- Kleiner 2007, p. 100
- Pratt 2022, § 5. Algebraization of Mathematics
- ↑
- Kleiner 2007, p. 100
- Pratt 2022, § 5. Algebraization of Mathematics
- Maddocks 2008, p. 130
- ↑
- Pratt 2022, § 5.1 Algebraic Geometry
- Danilov 2006, pp. 172, 174
- ↑
- Pratt 2022, § 5.3 Algebraic Topology
- Rabadan & Blumberg 2019, pp. 49–50
- Nakahara 2018, p. 121
- Weisstein 2003, pp. 52–53
- ↑
- Pratt 2022, § 5.2 Algebraic Number Theory
- Jarvis 2014, p. 1
- Viterbo & Hong 2011, p. 127
- ↑
- Kilty & McAllister 2018, pp. x, 347, 589
- Edwards 2012, pp. ix–x
- ↑
- ↑ Hintikka 2019, Lead Section, § Nature and Varieties of Logic
- ↑
- Halmos 1956, p. 363
- Burris & Legris 2021, § 1. Introduction
- ↑ Andréka, Németi & Sain 2001, pp. 133–134
- ↑
- EoM Staff 2020b, § Concrete Algebraic Logic
- Pratt 2022, § 5.4 Algebraic Logic
- Plotkin 2012, pp. 155–156
- Jansana 2022, Lead Section
- ↑ McGrath & Frank 2023, Lead Section
- ↑
- Boschini, Hansen & Wolf 2022, p. 21
- Brody 2006, pp. 535–536
- Franks 2023, Lead Section
- ↑
- EoM Staff 2020b, § Concrete Algebraic Logic
- Plotkin 2012, pp. 155–156
- Kachroo & Özbay 2018, pp. 176–177
- ↑
- EoM Staff 2020b, § Abstract Algebraic Logic
- Jansana 2022, § 4. Algebras
- ↑ 106.0 106.1 Gardella & DeLucia 2020, pp. 19–22
- ↑
- Arcavi, Drijvers & Stacey 2016, p. xiii
- Dekker & Dolk 2011, p. 69
- ↑
- ↑
- Arcavi, Drijvers & Stacey 2016, pp. 58–59
- Drijvers, Goddijn & Kindt 2011, p. 13
Sources
- Andréka, H.; Németi, I.; Sain, I. (2001). "Algebraic Logic" (in en). Handbook of Philosophical Logic. Springer Netherlands. ISBN 978-94-017-0452-6. https://link.springer.com/chapter/10.1007/978-94-017-0452-6_3. Retrieved 2024-01-24.
- Andrilli, Stephen; Hecker, David (2022) (in en). Elementary Linear Algebra. Academic Press. ISBN 978-0-323-98426-3. https://books.google.com/books?id=WtpVEAAAQBAJ&pg=PA57. Retrieved 2024-01-18.
- Anton, Howard; Rorres, Chris (2013) (in en). Elementary Linear Algebra: Applications Version. John Wiley & Sons. ISBN 978-1-118-47422-8. https://books.google.com/books?id=D9xoDwAAQBAJ. Retrieved 2024-01-18.
- Anton, Howard (2013) (in en). Elementary Linear Algebra. John Wiley & Sons. ISBN 978-1-118-67730-8. https://books.google.com/books?id=neYGCwAAQBAJ&pg=PA255. Retrieved 2024-01-18.
- Arcavi, Abraham; Drijvers, Paul; Stacey, Kaye (2016) (in en). The Learning and Teaching of Algebra: Ideas, Insights and Activities. Routledge. ISBN 978-1-134-82077-1. https://books.google.com/books?id=XGR9DAAAQBAJ. Retrieved 2024-01-24.
- Artamonov, V. A. (2003). "Quasivarieties". in Hazewinkel, M. (in en). Handbook of Algebra. Elsevier. ISBN 978-0-08-053297-4. https://books.google.com/books?id=sLDGY4Hk8V0C&pg=PA873. Retrieved 2024-01-21.
- Axler, Sheldon (2011) (in en). Algebra and Trigonometry. John Wiley & Sons. ISBN 978-0-470-58579-5. https://books.google.com/books?id=B5RxDwAAQBAJ&pg=PA7. Retrieved 2024-01-16.
- Barrera-Mora, Fernando (2023) (in en). Linear Algebra: A Minimal Polynomial Approach to Eigen Theory. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-113591-5. https://books.google.com/books?id=Xmu8EAAAQBAJ&pg=PR9. Retrieved 2024-01-18.
- Benson, Donald C. (2003) (in en). A Smoother Pebble: Mathematical Explorations. Oxford University Press. ISBN 978-0-19-514436-9. https://books.google.com/books?id=nNbnCwAAQBAJ&pg=PA111. Retrieved 2024-01-16.
- Berggren, John L. (2015). "Elementary Algebra" (in en). https://www.britannica.com/science/elementary-algebra.
- Boschini, Cecilia; Hansen, Arne; Wolf, Stefan (2022) (in en). Discrete Mathematics. vdf Hochschulverlag ETH Zürich. ISBN 978-3-7281-4110-1. https://books.google.com/books?id=huZtEAAAQBAJ&pg=PA21. Retrieved 2024-01-24.
- Boyer, Carl B.; Merzbach, Uta C. (2011) (in en). A History of Mathematics. John Wiley & Sons. ISBN 978-0-470-63056-3. https://books.google.com/books?id=bR9HAAAAQBAJ&pg=PA161. Retrieved 2024-01-27.
- Brody, Boruch A. (2006). Encyclopedia of Philosophy. 5. Donald M. Borchert (2nd ed.). Thomson Gale/Macmillan Reference US. pp. 535–536. ISBN 978-0-02-865780-6. OCLC 61151356.
- Burgin, Mark (2022) (in en). Trilogy Of Numbers And Arithmetic - Book 1: History Of Numbers And Arithmetic: An Information Perspective. World Scientific. ISBN 978-981-12-3685-3. https://books.google.com/books?id=rWF2EAAAQBAJ&pg=PA45. Retrieved 2024-01-13.
- Burris, Stanley; Legris, Javier (2021). "The Algebra of Logic Tradition". Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/entries/algebra-logic-tradition/.
- Buthusiem, Gregory; Toth, Gabor (2020) (in en). Precalculus. Linus Learning. ISBN 978-1-60797-798-8. https://books.google.com/books?id=a3QeEAAAQBAJ&pg=PA25. Retrieved 2024-01-16.
- Chang, C. C.; Keisler, H. J. (1990) (in en). Model Theory. Elsevier. ISBN 978-0-08-088007-5. https://books.google.com/books?id=uiHq0EmaFp0C&pg=PA603. Retrieved 2024-01-27.
- Cooper, Ellis D. (2011) (in en). Mathematical Mechanics: From Particle to Muscle. World Scientific. ISBN 978-981-4289-70-2. https://books.google.com/books?id=Fybzl6QB62gC&pg=PA60. Retrieved 2024-01-20.
- Corrochano, Eduardo Bayro; Sobczyk, Garret (2011) (in en). Geometric Algebra with Applications in Science and Engineering. Springer Science & Business Media. ISBN 978-1-4612-0159-5. https://books.google.com/books?id=GUHhBwAAQBAJ&pg=PR17. Retrieved 2024-01-24.
- Corry, Leo (2024). "Algebra" (in en). https://www.britannica.com/science/algebra.
- Cox, David A.; Little, John; O'Shea, Donal (2015) (in en). Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra. Springer. ISBN 978-3-319-16721-3. https://books.google.com/books?id=yL7yCAAAQBAJ&pg=PA268. Retrieved 2024-01-21.
- Cresswell, Julia (2010) (in en). Oxford Dictionary of Word Origins. OUP Oxford. ISBN 978-0-19-954793-7. https://books.google.com/books?id=J4i3zV4vnBAC&pg=PA11. Retrieved 2024-01-27.
- Danilov, V. I. (2006). "II. Algebraic Varieties and Schemes" (in en). Algebraic Geometry I: Algebraic Curves, Algebraic Manifolds and Schemes. Springer Science & Business Media. ISBN 978-3-540-51995-9. https://books.google.com/books?id=-QMWR-x66XUC&pg=PA172. Retrieved 2024-01-24.
- Dekker, Truus; Dolk, Maarten (2011). "3. From Arithmetic to Algebra". in Drijvers, Paul (in en). Secondary Algebra Education: Revisiting Topics and Themes and Exploring the Unknown. Springer Science & Business Media. ISBN 978-94-6091-334-1. https://books.google.com/books?id=7sVFaMhwackC&pg=PA5. Retrieved 2024-01-24.
- Derbyshire, John (2006). "2. The Father of Algebra" (in en). Unknown Quantity: A Real and Imaginary History of Algebra. National Academies Press. ISBN 978-0-309-09657-7. https://books.google.com/books?id=mLqaAgAAQBAJ&pg=PT39. Retrieved 2024-01-27.
- Dominich, Sándor (2008) (in en). The Modern Algebra of Information Retrieval. Springer Science & Business Media. ISBN 978-3-540-77659-8. https://books.google.com/books?id=uEedNKV3nlUC&pg=PA19. Retrieved 2024-01-20.
- Drijvers, Paul; Goddijn, Aad; Kindt, Martin (2011). "1. Algebra Education: Exploring Topics and Themes". in Drijvers, Paul (in en). Secondary Algebra Education: Revisiting Topics and Themes and Exploring the Unknown. Springer Science & Business Media. ISBN 978-94-6091-334-1. https://books.google.com/books?id=7sVFaMhwackC&pg=PA5. Retrieved 2024-01-24.
- Edwards, C. H. (2012) (in en). Advanced Calculus of Several Variables. Courier Corporation. ISBN 978-0-486-13195-5. https://books.google.com/books?id=sZIFcJ8DJAIC&pg=PR9. Retrieved 2024-01-24.
- Emch, Gerard G.; Sridharan, R.; Srinivas, M. D. (2005) (in en). Contributions to the History of Indian Mathematics. Springer. ISBN 978-93-86279-25-5. https://books.google.com/books?id=qfJdDwAAQBAJ&pg=PA20. Retrieved 2024-01-27.
- Jr, Everett Jenkins (2010) (in en). The Muslim Diaspora (Volume 1, 570-1500): A Comprehensive Chronology of the Spread of Islam in Asia, Africa, Europe and the Americas. McFarland. ISBN 978-0-7864-4713-8. https://books.google.com/books?id=giEkCQAAQBAJ&pg=PA82. Retrieved 2024-01-28.
- "Arithmetic". Springer. 2020a. https://encyclopediaofmath.org/wiki/Arithmetic.
- "Algebra". Springer. 2017. https://encyclopediaofmath.org/wiki/Algebra.
- "Algebra(2)". Springer. 2020. https://encyclopediaofmath.org/wiki/Algebra(2).
- "Algebraic Operation". Springer. 2023. https://encyclopediaofmath.org/wiki/Algebraic_operation.
- "Linear Equation". Springer. 2011. https://encyclopediaofmath.org/wiki/Linear_equation.
- "Ring". Springer. 2016a. https://encyclopediaofmath.org/wiki/Ring.
- "Group". Springer. 2016. https://encyclopediaofmath.org/wiki/Group.
- "Algebraic Logic". Springer. 2020b. https://encyclopediaofmath.org/wiki/Algebraic_logic.
- Fiche, Georges; Hebuterne, Gerard (2013) (in en). Mathematics for Engineers. John Wiley & Sons. ISBN 978-1-118-62333-6. https://books.google.com/books?id=TqkckiuuXg8C&pg=PT326. Retrieved 2024-01-13.
- Franks, Curtis (2023). "Propositional Logic". Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/entries/logic-propositional/.
- Gardella, Francis; DeLucia, Maria (2020) (in en). Algebra for the Middle Grades. IAP. ISBN 978-1-64113-847-5. https://books.google.com/books?id=HBXFDwAAQBAJ&pg=PA19. Retrieved 2024-01-24.
- Gilbert, William J.; Nicholson, W. Keith (2004) (in en). Modern Algebra with Applications. John Wiley & Sons. ISBN 978-0-471-46989-6. https://books.google.com/books?id=paINAXYHN8kC&pg=PA4. Retrieved 2024-01-13.
- Golan, Jonathan S. (1995). "Algebras Over A Field" (in en). Foundations of Linear Algebra. Springer Netherlands. ISBN 978-94-015-8502-6. https://link.springer.com/chapter/10.1007/978-94-015-8502-6_18. Retrieved 2024-01-13.
- Grätzer, George (2008) (in en). Universal Algebra (2 ed.). Springer Science & Business Media. ISBN 978-0-387-77487-9. https://books.google.com/books?id=8lNkXPJas4wC. Retrieved 2024-01-27.
- Grillet, Pierre Antoine (2007). "Universal Algebra" (in en). Abstract Algebra. Springer. ISBN 978-0-387-71568-1. https://link.springer.com/chapter/10.1007/978-0-387-71568-1_15. Retrieved 2024-01-13.
- Halmos, Paul R. (1956). "The Basic Concepts of Algebraic Logic". The American Mathematical Monthly 63 (6). doi:10.2307/2309396. ISSN 0002-9890.
- Harrison, Michael; Waldron, Patrick (2011) (in en). Mathematics for Economics and Finance. Routledge. ISBN 978-1-136-81921-6. https://books.google.com/books?id=_sisAgAAQBAJ&pg=PT464. Retrieved 2024-01-18.
- Hazewinkel, Michiel (1994) (in en). Encyclopaedia of Mathematics (Set). Springer Science & Business Media. ISBN 978-1-55608-010-4. https://books.google.com/books?id=PE1a-EIG22kC&pg=PA73. Retrieved 2024-01-27.
- "Arithmetic". HarperCollins. 2022. https://www.ahdictionary.com/word/search.html?q=arithmetic&submit.x=58&submit.y=14.
- Higgins, Peter M. (2015) (in en). Algebra: A Very Short Introduction. OUP Oxford. ISBN 978-0-19-104746-6. https://books.google.com/books?id=QANiCgAAQBAJ&pg=PA89. Retrieved 2024-01-27.
- Hintikka, Jaakko J. (2019). "Philosophy of Logic" (in en). https://www.britannica.com/topic/philosophy-of-logic.
- Hoad, T. F. (1993). The Concise Oxford Dictionary of English Etymology. Oxford University Press. ISBN 978-0-19-283098-2.
- Igarashi, Yoshihide; Altman, Tom; Funada, Mariko; Kamiyama, Barbara (2014) (in en). Computing: A Historical and Technical Perspective. CRC Press. ISBN 978-1-4822-2741-3. https://books.google.com/books?id=58ySAwAAQBAJ&pg=PA103.
- Indurkhya, Bipin (2013). "6.5 Algebras and Structures" (in en). Metaphor and Cognition: An Interactionist Approach. Springer Science & Business Media. ISBN 978-94-017-2252-0. https://books.google.com/books?id=foTrCAAAQBAJ&pg=PA217. Retrieved 2024-01-21.
- Insall, Matt; Sakharov, Alex. "Universal Algebra" (in en). Wolfram. https://mathworld.wolfram.com/UniversalAlgebra.html.
- Irving, Ronald S. (2004) (in en). Integers, Polynomials, and Rings: A Course in Algebra. Springer Science & Business Media. ISBN 978-0-387-40397-7. https://books.google.com/books?id=-7OM1OtOFJgC. Retrieved 2024-01-20.
- Jansana, Ramon (2022). "Algebraic Propositional Logic". Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/entries/logic-algebraic-propositional/.
- Jarvis, Frazer (2014) (in en). Algebraic Number Theory. Springer. ISBN 978-3-319-07545-7. https://books.google.com/books?id=0j0qBAAAQBAJ&pg=PA1. Retrieved 2024-01-24.
- Kachroo, Pushkin; Özbay, Kaan M. A. (2018) (in en). Feedback Control Theory for Dynamic Traffic Assignment. Springer. ISBN 978-3-319-69231-9. https://books.google.com/books?id=qQNbDwAAQBAJ&pg=PA176. Retrieved 2024-01-24.
- Khattar, Dinesh; Agrawal, Neha (2023) (in en). Group Theory. Springer Nature. ISBN 978-3-031-21307-6. https://books.google.com/books?id=7-nIEAAAQBAJ&pg=PA4. Retrieved 2024-01-20.
- Kilty, Joel; McAllister, Alex (2018) (in en). Mathematical Modeling and Applied Calculus. Oxford University Press. ISBN 978-0-19-255813-8. https://books.google.com/books?id=YVRuDwAAQBAJ&pg=PA347. Retrieved 2024-01-24.
- Kleiner, Israel (2007) (in en). A History of Abstract Algebra. Springer Science & Business Media. ISBN 978-0-8176-4685-1. https://books.google.com/books?id=udj-1UuaOiIC&pg=PA100. Retrieved 2024-01-24.
- Knoebel, Arthur (2011) (in en). Sheaves of Algebras Over Boolean Spaces. Springer Science & Business Media. ISBN 978-0-8176-4218-1. https://books.google.com/books?id=VWS_sgO2uvgC&pg=PA5. Retrieved 2024-01-27.
- Kramer, Jürg; Pippich, Anna-Maria von (2017) (in en). From Natural Numbers to Quaternions. Springer. ISBN 978-3-319-69429-0. https://books.google.com/books?id=nvM-DwAAQBAJ&pg=PA49. Retrieved 2024-01-20.
- Kvasz, L. (2006). "The History of Algebra and the Development of the Form of Its Language". Philosophia Mathematica 14 (3). doi:10.1093/philmat/nkj017.
- Lamagna, Edmund A. (2019) (in en). Computer Algebra: Concepts and Techniques. CRC Press. ISBN 978-1-351-60583-0. https://books.google.com/books?id=8PSDDwAAQBAJ&pg=PA150. Retrieved 2024-01-16.
- Maddocks, J. R. (2008). "Algebra". in Lerner, Brenda Wilmoth; Lerner, K. Lee. The Gale Encyclopedia of Science (4th ed.). Thompson Gale. ISBN 978-1-4144-2877-2. https://www.encyclopedia.com/science-and-technology/mathematics/mathematics/algebra. Retrieved 2024-01-13.
- Majewski, Miroslaw (2004). MuPAD Pro Computing Essentials (2 ed.). Springer. ISBN 978-3-540-21943-9.
- Mal’cev, A. I. (1973). "Quasivarieties" (in en). Algebraic Systems. Springer. ISBN 978-3-642-65374-2. https://link.springer.com/chapter/10.1007/978-3-642-65374-2_5. Retrieved 2024-01-21.
- Mancosu, Paolo (1999) (in en). Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century. Oxford University Press. ISBN 978-0-19-513244-1. https://books.google.com/books?id=60qaEePdqcoC&pg=PA84. Retrieved 2024-01-24.
- Maxwell, E. A. (2009) (in en). Algebraic Structure and Matrices Book 2. Syracuse University Press. ISBN 978-0-521-10905-5. https://books.google.com/books?id=yD0irRUE_u4C&pg=PA73. Retrieved 2024-01-20.
- McGrath, Matthew; Frank, Devin (2023). "Propositions". Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/entries/propositions/.
- McKeague, Charles P. (2014) (in en). Intermediate Algebra: A Text/Workbook. Academic Press. ISBN 978-1-4832-1417-7. https://books.google.com/books?id=nI7iBQAAQBAJ&pg=PA386. Retrieved 2024-01-16.
- McWeeny, R. (2002) (in en). Symmetry: An Introduction to Group Theory and Its Applications. Courier Corporation. ISBN 978-0-486-42182-7. https://books.google.com/books?id=x3fjIXY93TsC&pg=PA6. Retrieved 2024-01-20.
- Menini, Claudia; Oystaeyen, Freddy Van (2017) (in en). Abstract Algebra: A Comprehensive Treatment. CRC Press. ISBN 978-1-4822-5817-2. https://books.google.com/books?id=3mlQDwAAQBAJ&pg=PA722. Retrieved 2024-01-27.
- Mortensen, C. E. (2013) (in en). Inconsistent Mathematics. Springer Science & Business Media. ISBN 978-94-015-8453-1. https://books.google.com/books?id=KYDrCAAAQBAJ&pg=PA73. Retrieved 2024-01-18.
- Musielak, Dora (2020) (in en). Sophie Germain: Revolutionary Mathematician. Springer Nature. ISBN 978-3-030-38375-6. https://books.google.com/books?id=iqHYDwAAQBAJ&pg=PA36. Retrieved 2024-01-27.
- "Definition of Arithmetic" (in en). 2023. https://www.merriam-webster.com/dictionary/arithmetic.
- Nakahara, Mikio (2018) (in en). Geometry, Topology and Physics. Taylor & Francis. ISBN 978-1-4200-5694-5. https://books.google.com/books?id=p2C1DwAAQBAJ&pg=PA121. Retrieved 2024-01-24.
- Negro, Luca Dal (2022) (in en). Waves in Complex Media. Cambridge University Press. ISBN 978-1-107-03750-2. https://books.google.com/books?id=MIdoEAAAQBAJ&pg=PA365. Retrieved 2024-01-21.
- Neri, Ferrante (2019) (in en). Linear Algebra for Computational Sciences and Engineering. Springer. ISBN 978-3-030-21321-3. https://books.google.com/books?id=NMOlDwAAQBAJ&pg=PR12. Retrieved 2024-01-24.
- OUP Staff. "Algebra". Oxford University Press. http://www.lexico.com/definition/algebra.
- Ovchinnikov, Sergei (2015) (in en). Number Systems. American Mathematical Society. ISBN 978-1-4704-2018-5. https://books.google.com/books?id=UMbXBgAAQBAJ&pg=PA27. Retrieved 2024-01-20.
- Pickover, Clifford A. (2009) (in en). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling Publishing Company, Inc.. ISBN 978-1-4027-5796-9. https://books.google.com/books?id=JrslMKTgSZwC&pg=PA90. Retrieved 2024-01-28.
- Plotkin, B. (2012) (in en). Universal Algebra, Algebraic Logic, and Databases. Springer Science & Business Media. ISBN 978-94-011-0820-1. https://books.google.com/books?id=-v3xCAAAQBAJ&pg=PA155. Retrieved 2024-01-24.
- Pratt, Vaughan (2022). "Algebra". Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/entries/algebra/.
- Rabadan, Raul; Blumberg, Andrew J. (2019) (in en). Topological Data Analysis for Genomics and Evolution: Topology in Biology. Cambridge University Press. ISBN 978-1-107-15954-9. https://books.google.com/books?id=2967DwAAQBAJ&pg=PA49. Retrieved 2024-01-24.
- Renze, John; Weisstein, Eric W.. "Algebra" (in en). Wolfram. https://mathworld.wolfram.com/Algebra.html.
- Rohde, Ulrich L.; Jain, G. C.; Poddar, Ajay K.; Ghosh, A. K. (2012) (in en). Introduction to Differential Calculus: Systematic Studies with Engineering Applications for Beginners. John Wiley & Sons. ISBN 978-1-118-13014-8. https://books.google.com/books?id=vk2XbZpsBOwC&pg=PT89. Retrieved 2024-01-16.
- Romanowski, Perry (2008). "Arithmetic". in Lerner, Brenda Wilmoth; Lerner, K. Lee. The Gale Encyclopedia of Science (4th ed.). Thompson Gale. ISBN 978-1-4144-2877-2. https://www.encyclopedia.com/science-and-technology/mathematics/mathematics/arithmetic. Retrieved 2024-01-13.
- Rowland, Todd; Weisstein, Eric W.. "Group" (in en). Wolfram. https://mathworld.wolfram.com/Group.html.
- Seshadri, C. S. (2010) (in en). Studies in the History of Indian Mathematics. Springer. ISBN 978-93-86279-49-1. https://books.google.com/books?id=w_JdDwAAQBAJ&pg=PA156. Retrieved 2024-01-27.
- Sialaros, Michalis (2018) (in en). Revolutions and Continuity in Greek Mathematics. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-056527-0. https://books.google.com/books?id=2PZYDwAAQBAJ&pg=PT55. Retrieved 2024-01-27.
- Silvia, M. T.; Robinson, E. A. (1979) (in en). Deconvolution of Geophysical Time Series in the Exploration for Oil and Natural Gas. Elsevier. ISBN 978-0-08-086864-6. https://books.google.com/books?id=Ecgfjh-MpU0C&pg=PA82. Retrieved 2024-01-21.
- Smorynski, Craig (2007) (in en). History of Mathematics: A Supplement. Springer Science & Business Media. ISBN 978-0-387-75481-9. https://books.google.com/books?id=qY657eFq7UgC&pg=PA137. Retrieved 2024-01-27.
- Sullivan, Michael (2010) (in en). Finite Mathematics: An Applied Approach. John Wiley & Sons. ISBN 978-0-470-87639-8. https://books.google.com/books?id=6NKaDwAAQBAJ&pg=PA53. Retrieved 2024-01-18.
- Sun, Shuyu; Zhang, Tao (2020) (in en). Reservoir Simulations: Machine Learning and Modeling. Gulf Professional Publishing. ISBN 978-0-12-820962-2. https://books.google.com/books?id=SZ3hDwAAQBAJ&pg=PA94.
- Tan, Kiat Shi; Steeb, Willi-Hans; Hardy, Yorick (2012) (in en). SymbolicC++:An Introduction to Computer Algebra Using Object-Oriented Programming: An Introduction to Computer Algebra Using Object-Oriented Programming. Springer Science & Business Media. ISBN 978-1-4471-0405-6. https://books.google.com/books?id=UDb0BwAAQBAJ&pg=PA306. Retrieved 2024-01-16.
- Tanton, James (2005). Encyclopedia of Mathematics. Facts On File. ISBN 978-0-8160-5124-3.
- Terr, David; Weisstein, Eric W.. "Ring of Integers" (in en). Wolfram. https://mathworld.wolfram.com/RingofIntegers.html.
- Viterbo, Emanuele; Hong, Yi (2011). "3.4 Algebraic Number Theory". in Hlawatsch, Franz; Matz, Gerald (in en). Wireless Communications Over Rapidly Time-Varying Channels. Academic Press. ISBN 978-0-08-092272-0. https://books.google.com/books?id=d89QRR24jbMC&pg=PA127. Retrieved 2024-01-24.
- Waerden, Bartel L. van der (2013) (in en). A History of Algebra: From al-Khwārizmī to Emmy Noether. Springer Science & Business Media. ISBN 978-3-642-51599-6. https://books.google.com/books?id=W6DwCAAAQBAJ. Retrieved 2024-01-27.
- Wagner, Sigrid; Kieran, Carolyn (2018) (in en). Research Issues in the Learning and Teaching of Algebra: The Research Agenda for Mathematics Education, Volume 4. Routledge. ISBN 978-1-135-43421-2. https://books.google.com/books?id=uW4ECwAAQBAJ&pg=PT225. Retrieved 2024-01-13.
- Walz, Guido (2016). "Algebra" (in de). Lexikon der Mathematik: Band 1: A bis Eif. Springer-Verlag. ISBN 978-3-662-53498-4. https://www.spektrum.de/lexikon/mathematik/algebra/12062. Retrieved 2024-01-13.
- Weisstein, Eric W. (2003). CRC Concise Encyclopedia of Mathematics (2nd ed.). Chapman & Hall/CRC. ISBN 978-1-58488-347-0.
- Weisstein, Eric W. (2024a). "Field" (in en). Wolfram. https://mathworld.wolfram.com/Field.html.
- Weisstein, Eric W. (2024b). "Field Axioms" (in en). Wolfram. https://mathworld.wolfram.com/FieldAxioms.html.
- Weisstein, Eric W. (2024c). "Ring" (in en). Wolfram. https://mathworld.wolfram.com/Ring.html.
- Williams, Gareth (2007) (in en). Linear Algebra with Applications. Jones & Bartlett Learning. ISBN 978-0-7637-5753-3. https://books.google.com/books?id=HLQ9ocWuCzMC&pg=PA4. Retrieved 2024-01-18.
- Young, Cynthia Y. (2010) (in en). Precalculus. John Wiley & Sons. ISBN 978-0-471-75684-2. https://books.google.com/books?id=9HRLAn326zEC&pg=RA1-PA999. Retrieved 2024-01-16.
- Young, Cynthia Y. (2023) (in en). Precalculus. John Wiley & Sons. ISBN 978-1-119-86940-5. https://books.google.com/books?id=pMSZEAAAQBAJ&pg=PA714. Retrieved 2024-01-18.
- Zill, Dennis; Dewar, Jacqueline (2011) (in en). Algebra and Trigonometry. Jones & Bartlett Publishers. ISBN 978-0-7637-5461-7. https://books.google.com/books?id=MBAwrjc3gqMC&pg=PA529. Retrieved 2024-01-16.
- Zwillinger, Daniel (2002) (in en). CRC Standard Mathematical Tables and Formulae. CRC Press. ISBN 978-1-4200-3534-6. https://books.google.com/books?id=gE_MBQAAQBAJ&pg=PA812. Retrieved 2024-01-27.
External links
| Wikisource has the text of the 1911 Encyclopædia Britannica article Algebra. |
 |