Periodic points of complex quadratic mappings

This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length. These periodic points play a role in the theories of Fatou and Julia sets.

Definitions

Let

[math]\displaystyle{ f_c(z) = z^2+c\, }[/math]

be the complex quadric mapping, where [math]\displaystyle{ z }[/math] and [math]\displaystyle{ c }[/math] are complex numbers.

Notationally, [math]\displaystyle{ f^{(k)} _c (z) }[/math] is the [math]\displaystyle{ k }[/math]-fold composition of [math]\displaystyle{ f_c }[/math] with itself (not to be confused with the [math]\displaystyle{ k }[/math]th derivative of [math]\displaystyle{ f_c }[/math])—that is, the value after the k-th iteration of the function [math]\displaystyle{ f _c. }[/math] Thus

[math]\displaystyle{ f^{(k)} _c (z) = f_c(f^{(k-1)} _c (z)). }[/math]

Periodic points of a complex quadratic mapping of period [math]\displaystyle{ p }[/math] are points [math]\displaystyle{ z }[/math] of the dynamical plane such that

[math]\displaystyle{ f^{(p)} _c (z) = z, }[/math]

where [math]\displaystyle{ p }[/math] is the smallest positive integer for which the equation holds at that z.

We can introduce a new function:

[math]\displaystyle{ F_p(z,f) = f^{(p)} _c (z) - z, }[/math]

so periodic points are zeros of function [math]\displaystyle{ F_p(z,f) }[/math]: points z satisfying

[math]\displaystyle{ F_p(z,f) = 0, }[/math]

which is a polynomial of degree [math]\displaystyle{ 2^p. }[/math]

Number of periodic points

The degree of the polynomial [math]\displaystyle{ F_p(z,f) }[/math] describing periodic points is [math]\displaystyle{ d = 2^p }[/math] so it has exactly [math]\displaystyle{ d = 2^p }[/math] complex roots (= periodic points), counted with multiplicity.

Stability of periodic points (orbit) - multiplier

Stability index of periodic points along horizontal axis

boundaries of regions of parameter plane with attracting orbit of periods 1-6

Critical orbit of discrete dynamical system based on complex quadratic polynomial. It tends to weakly attracting fixed point with abs(multiplier) = 0.99993612384259

The multiplier (or eigenvalue, derivative) [math]\displaystyle{ m(f^p,z_0)=\lambda }[/math] of a rational map [math]\displaystyle{ f }[/math] iterated [math]\displaystyle{ p }[/math] times at cyclic point [math]\displaystyle{ z_0 }[/math] is defined as:

[math]\displaystyle{ m(f^p,z_0) = \lambda = \begin{cases} f^{p \prime}(z_0), &\mbox{if }z_0 \ne \infty \\ \frac{1}{f^{p \prime} (z_0)}, & \mbox{if }z_0 = \infty \end{cases} }[/math]

where [math]\displaystyle{ f^{p\prime} (z_0) }[/math] is the first derivative of [math]\displaystyle{ f^p }[/math] with respect to [math]\displaystyle{ z }[/math] at [math]\displaystyle{ z_0 }[/math].

Because the multiplier is the same at all periodic points on a given orbit, it is called a multiplier of the periodic orbit.

The multiplier is:

• a complex number;
• invariant under conjugation of any rational map at its fixed point;
• used to check stability of periodic (also fixed) points with stability index [math]\displaystyle{ abs(\lambda). \, }[/math]

A periodic point is

• attracting when [math]\displaystyle{ abs(\lambda) \lt 1; }[/math]
  • super-attracting when [math]\displaystyle{ abs(\lambda) = 0; }[/math]
  • attracting but not super-attracting when [math]\displaystyle{ 0 \lt abs(\lambda) \lt 1; }[/math]
• indifferent when [math]\displaystyle{ abs(\lambda) = 1; }[/math]
  • rationally indifferent or parabolic if [math]\displaystyle{ \lambda }[/math] is a root of unity;
  • irrationally indifferent if [math]\displaystyle{ abs(\lambda)=1 }[/math] but multiplier is not a root of unity;
• repelling when [math]\displaystyle{ abs(\lambda) \gt 1. }[/math]

Periodic points

• that are attracting are always in the Fatou set;
• that are repelling are in the Julia set;
• that are indifferent fixed points may be in one or the other. A parabolic periodic point is in the Julia set.

Period-1 points (fixed points)

Finite fixed points

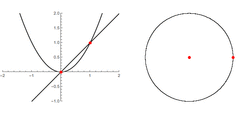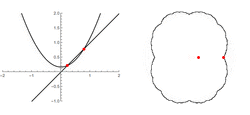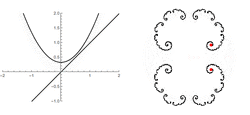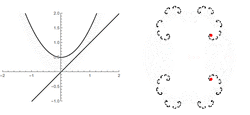
Let us begin by finding all finite points left unchanged by one application of [math]\displaystyle{ f }[/math]. These are the points that satisfy [math]\displaystyle{ f_c(z)=z }[/math]. That is, we wish to solve

[math]\displaystyle{ z^2+c=z,\, }[/math]

which can be rewritten as

[math]\displaystyle{ \ z^2-z+c=0. }[/math]

Since this is an ordinary quadratic equation in one unknown, we can apply the standard quadratic solution formula:

[math]\displaystyle{ \alpha_1 = \frac{1-\sqrt{1-4c}}{2} }[/math] and [math]\displaystyle{ \alpha_2 = \frac{1+\sqrt{1-4c}}{2}. }[/math]

So for [math]\displaystyle{ c \in \mathbb{C} \setminus \{1/4\} }[/math] we have two finite fixed points [math]\displaystyle{ \alpha_1 }[/math] and [math]\displaystyle{ \alpha_2 }[/math].

Since

[math]\displaystyle{ \alpha_1 = \frac{1}{2}-m }[/math] and [math]\displaystyle{ \alpha_2 = \frac{1}{2}+m }[/math] where [math]\displaystyle{ m = \frac{\sqrt{1-4c}}{2}, }[/math]

we have [math]\displaystyle{ \alpha_1 + \alpha_2 = 1 }[/math].

Thus fixed points are symmetrical about [math]\displaystyle{ z = 1/2 }[/math].

This image shows fixed points (both repelling)

Complex dynamics

Fixed points for c along horizontal axis

Fatou set for F(z) = z*z with marked fixed point

Here different notation is commonly used:

[math]\displaystyle{ \alpha_c = \frac{1-\sqrt{1-4c}}{2} }[/math] with multiplier [math]\displaystyle{ \lambda_{\alpha_c} = 1-\sqrt{1-4c} }[/math]

and

[math]\displaystyle{ \beta_c = \frac{1+\sqrt{1-4c}}{2} }[/math] with multiplier [math]\displaystyle{ \lambda_{\beta_c} = 1+\sqrt{1-4c}. }[/math]

Again we have

[math]\displaystyle{ \alpha_c + \beta_c = 1 . }[/math]

Since the derivative with respect to z is

[math]\displaystyle{ P_c'(z) = \frac{d}{dz}P_c(z) = 2z , }[/math]

we have

[math]\displaystyle{ P_c'(\alpha_c) + P_c'(\beta_c)= 2 \alpha_c + 2 \beta_c = 2 (\alpha_c + \beta_c) = 2 . }[/math]

This implies that [math]\displaystyle{ P_c }[/math] can have at most one attractive fixed point.

These points are distinguished by the facts that:

• [math]\displaystyle{ \beta_c }[/math] is:
  • the landing point of the external ray for angle=0 for [math]\displaystyle{ c \in M \setminus \left\{ 1/4 \right\} }[/math]
  • the most repelling fixed point of the Julia set
  • the one on the right (whenever fixed point are not symmetrical around the real axis), it is the extreme right point for connected Julia sets (except for cauliflower).
• [math]\displaystyle{ \alpha_c }[/math] is:
  • the landing point of several rays
  • attracting when [math]\displaystyle{ c }[/math] is in the main cardioid of the Mandelbrot set, in which case it is in the interior of a filled-in Julia set, and therefore belongs to the Fatou set (strictly to the basin of attraction of finite fixed point)
  • parabolic at the root point of the limb of the Mandelbrot set
  • repelling for other values of [math]\displaystyle{ c }[/math]

Special cases

An important case of the quadratic mapping is [math]\displaystyle{ c=0 }[/math]. In this case, we get [math]\displaystyle{ \alpha_1 = 0 }[/math] and [math]\displaystyle{ \alpha_2=1 }[/math]. In this case, 0 is a superattractive fixed point, and 1 belongs to the Julia set.

Only one fixed point

We have [math]\displaystyle{ \alpha_1=\alpha_2 }[/math] exactly when [math]\displaystyle{ 1-4c=0. }[/math] This equation has one solution, [math]\displaystyle{ c=1/4, }[/math] in which case [math]\displaystyle{ \alpha_1=\alpha_2=1/2 }[/math]. In fact [math]\displaystyle{ c=1/4 }[/math] is the largest positive, purely real value for which a finite attractor exists.

Infinite fixed point

We can extend the complex plane [math]\displaystyle{ \mathbb{C} }[/math] to the Riemann sphere (extended complex plane) [math]\displaystyle{ \mathbb{\hat{C}} }[/math] by adding infinity:

[math]\displaystyle{ \mathbb{\hat{C}} = \mathbb{C} \cup \{ \infty \} }[/math]

and extend [math]\displaystyle{ f_c }[/math] such that [math]\displaystyle{ f_c(\infty)=\infty. }[/math]

Then infinity is:

• superattracting
• a fixed point of [math]\displaystyle{ f_c }[/math]:[math]\displaystyle{ f_c(\infty)=\infty=f^{-1}_c(\infty). }[/math]

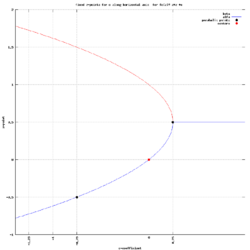
Period-2 cycles

Bifurcation from period 1 to 2 for complex quadratic map

Bifurcation of periodic points from period 1 to 2 for fc(z)=z*z +c

Period-2 cycles are two distinct points [math]\displaystyle{ \beta_1 }[/math] and [math]\displaystyle{ \beta_2 }[/math] such that [math]\displaystyle{ f_c(\beta_1) = \beta_2 }[/math] and [math]\displaystyle{ f_c(\beta_2) = \beta_1 }[/math], and hence

[math]\displaystyle{ f_c(f_c(\beta_n)) = \beta_n }[/math]

for [math]\displaystyle{ n \in \{1, 2\} }[/math]:

[math]\displaystyle{ f_c(f_c(z)) = (z^2+c)^2+c = z^4 + 2cz^2 + c^2 + c. }[/math]

Equating this to z, we obtain

[math]\displaystyle{ z^4 + 2cz^2 - z + c^2 + c = 0. }[/math]

This equation is a polynomial of degree 4, and so has four (possibly non-distinct) solutions. However, we already know two of the solutions. They are [math]\displaystyle{ \alpha_1 }[/math] and [math]\displaystyle{ \alpha_2 }[/math], computed above, since if these points are left unchanged by one application of [math]\displaystyle{ f }[/math], then clearly they will be unchanged by more than one application of [math]\displaystyle{ f }[/math].

Our 4th-order polynomial can therefore be factored in 2 ways:

First method of factorization

[math]\displaystyle{ (z-\alpha_1)(z-\alpha_2)(z-\beta_1)(z-\beta_2) = 0.\, }[/math]

This expands directly as [math]\displaystyle{ x^4 - Ax^3 + Bx^2 - Cx + D = 0 }[/math] (note the alternating signs), where

[math]\displaystyle{ D = \alpha_1 \alpha_2 \beta_1 \beta_2, \, }[/math]

[math]\displaystyle{ C = \alpha_1 \alpha_2 \beta_1 + \alpha_1 \alpha_2 \beta_2 + \alpha_1 \beta_1 \beta_2 + \alpha_2 \beta_1 \beta_2, \, }[/math]

[math]\displaystyle{ B = \alpha_1 \alpha_2 + \alpha_1 \beta_1 + \alpha_1 \beta_2 + \alpha_2 \beta_1 + \alpha_2 \beta_2 + \beta_1 \beta_2, \, }[/math]

[math]\displaystyle{ A = \alpha_1 + \alpha_2 + \beta_1 + \beta_2.\, }[/math]

We already have two solutions, and only need the other two. Hence the problem is equivalent to solving a quadratic polynomial. In particular, note that

[math]\displaystyle{ \alpha_1 + \alpha_2 = \frac{1-\sqrt{1-4c}}{2} + \frac{1+\sqrt{1-4c}}{2} = \frac{1+1}{2} = 1 }[/math]

and

[math]\displaystyle{ \alpha_1 \alpha_2 = \frac{(1-\sqrt{1-4c})(1+\sqrt{1-4c})}{4} = \frac{1^2 - (\sqrt{1-4c})^2}{4}= \frac{1 - 1 + 4c}{4} = \frac{4c}{4} = c. }[/math]

Adding these to the above, we get [math]\displaystyle{ D = c \beta_1 \beta_2 }[/math] and [math]\displaystyle{ A = 1 + \beta_1 + \beta_2 }[/math]. Matching these against the coefficients from expanding [math]\displaystyle{ f }[/math], we get

[math]\displaystyle{ D = c \beta_1 \beta_2 = c^2 + c }[/math] and [math]\displaystyle{ A = 1 + \beta_1 + \beta_2 = 0. }[/math]

From this, we easily get

[math]\displaystyle{ \beta_1 \beta_2 = c + 1 }[/math] and [math]\displaystyle{ \beta_1 + \beta_2 = -1 }[/math].

From here, we construct a quadratic equation with [math]\displaystyle{ A' = 1, B = 1, C = c+1 }[/math] and apply the standard solution formula to get

[math]\displaystyle{ \beta_1 = \frac{-1 - \sqrt{-3 -4c}}{2} }[/math] and [math]\displaystyle{ \beta_2 = \frac{-1 + \sqrt{-3 -4c}}{2}. }[/math]

Closer examination shows that:

[math]\displaystyle{ f_c(\beta_1) = \beta_2 }[/math] and [math]\displaystyle{ f_c(\beta_2) = \beta_1, }[/math]

meaning these two points are the two points on a single period-2 cycle.

Second method of factorization

We can factor the quartic by using polynomial long division to divide out the factors [math]\displaystyle{ (z-\alpha_1) }[/math] and [math]\displaystyle{ (z-\alpha_2), }[/math] which account for the two fixed points [math]\displaystyle{ \alpha_1 }[/math] and [math]\displaystyle{ \alpha_2 }[/math] (whose values were given earlier and which still remain at the fixed point after two iterations):

[math]\displaystyle{ (z^2+c)^2 + c -z = (z^2 + c - z)(z^2 + z + c +1 ). \, }[/math]

The roots of the first factor are the two fixed points. They are repelling outside the main cardioid.

The second factor has the two roots

[math]\displaystyle{ \frac{-1 \pm \sqrt{-3 -4c}}{2}. \, }[/math]

These two roots, which are the same as those found by the first method, form the period-2 orbit.

Special cases

Again, let us look at [math]\displaystyle{ c=0 }[/math]. Then

[math]\displaystyle{ \beta_1 = \frac{-1 - i\sqrt{3}}{2} }[/math] and [math]\displaystyle{ \beta_2 = \frac{-1 + i\sqrt{3}}{2}, }[/math]

both of which are complex numbers. We have [math]\displaystyle{ | \beta_1 | = | \beta_2 | = 1 }[/math]. Thus, both these points are "hiding" in the Julia set. Another special case is [math]\displaystyle{ c=-1 }[/math], which gives [math]\displaystyle{ \beta_1 = 0 }[/math] and [math]\displaystyle{ \beta_2 = -1 }[/math]. This gives the well-known superattractive cycle found in the largest period-2 lobe of the quadratic Mandelbrot set.

Cycles for period greater than 2

Periodic points of f(z) = z*z−0.75 for period =6 as intersections of 2 implicit curves

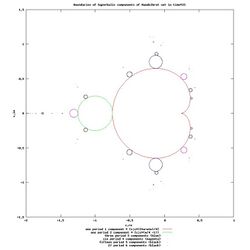
The degree of the equation [math]\displaystyle{ f^{(n)}(z)=z }[/math] is 2ⁿ; thus for example, to find the points on a 3-cycle we would need to solve an equation of degree 8. After factoring out the factors giving the two fixed points, we would have a sixth degree equation.

There is no general solution in radicals to polynomial equations of degree five or higher, so the points on a cycle of period greater than 2 must in general be computed using numerical methods. However, in the specific case of period 4 the cyclical points have lengthy expressions in radicals.

In the case c = –2, trigonometric solutions exist for the periodic points of all periods. The case [math]\displaystyle{ z_{n+1}=z_n^2-2 }[/math] is equivalent to the logistic map case r = 4: [math]\displaystyle{ x_{n+1}=4x_n(1-x_n). }[/math] Here the equivalence is given by [math]\displaystyle{ z=2-4x. }[/math] One of the k-cycles of the logistic variable x (all of which cycles are repelling) is

[math]\displaystyle{ \sin^2\left(\frac{2\pi}{2^k-1}\right), \, \sin^2\left(2\cdot\frac{2\pi}{2^k-1}\right), \, \sin^2\left(2^2\cdot\frac{2\pi}{2^k-1}\right), \, \sin^2\left(2^3\cdot\frac{2\pi}{2^k-1}\right), \dots , \sin^2\left(2^{k-1}\frac{2\pi}{2^k-1}\right). }[/math]

Further reading

• Geometrical properties of polynomial roots
• Alan F. Beardon, Iteration of Rational Functions, Springer 1991, ISBN:0-387-95151-2
• Michael F. Barnsley (Author), Stephen G. Demko (Editor), Chaotic Dynamics and Fractals (Notes and Reports in Mathematics in Science and Engineering Series) Academic Pr (April 1986), ISBN:0-12-079060-2
• Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002
• The permutations of periodic points in quadratic polynominials by J Leahy

External links

• Algebraic solution of Mandelbrot orbital boundaries by Donald D. Cross
• Brown Method by Robert P. Munafo
• arXiv:hep-th/0501235v2 V.Dolotin, A.Morozov: Algebraic Geometry of Discrete Dynamics. The case of one variable.