Periodic summation
In mathematics, any integrable function [math]\displaystyle{ s(t) }[/math] can be made into a periodic function [math]\displaystyle{ s_P(t) }[/math] with period P by summing the translations of the function [math]\displaystyle{ s(t) }[/math] by integer multiples of P. This is called periodic summation:
- [math]\displaystyle{ s_P(t) = \sum_{n=-\infty}^\infty s(t + nP) }[/math]
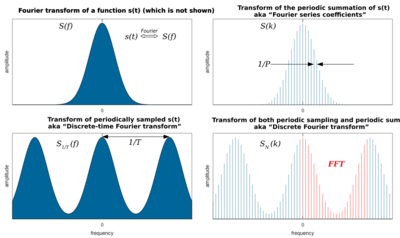
When [math]\displaystyle{ s_P(t) }[/math] is alternatively represented as a Fourier series, the Fourier coefficients are equal to the values of the continuous Fourier transform, [math]\displaystyle{ S(f) \triangleq \mathcal{F}\{s(t)\}, }[/math] at intervals of [math]\displaystyle{ \tfrac{1}{P} }[/math].[1][2] That identity is a form of the Poisson summation formula. Similarly, a Fourier series whose coefficients are samples of [math]\displaystyle{ s(t) }[/math] at constant intervals (T) is equivalent to a periodic summation of [math]\displaystyle{ S(f), }[/math] which is known as a discrete-time Fourier transform.
The periodic summation of a Dirac delta function is the Dirac comb. Likewise, the periodic summation of an integrable function is its convolution with the Dirac comb.
Quotient space as domain
If a periodic function is instead represented using the quotient space domain [math]\displaystyle{ \mathbb{R}/(P\mathbb{Z}) }[/math] then one can write:
- [math]\displaystyle{ \varphi_P : \mathbb{R}/(P\mathbb{Z}) \to \mathbb{R} }[/math]
- [math]\displaystyle{ \varphi_P(x) = \sum_{\tau\in x} s(\tau) ~ . }[/math]
The arguments of [math]\displaystyle{ \varphi_P }[/math] are equivalence classes of real numbers that share the same fractional part when divided by [math]\displaystyle{ P }[/math].
Citations
- ↑ Pinsky, Mark (2001). Introduction to Fourier Analysis and Wavelets. Brooks/Cole. ISBN 978-0534376604.
- ↑ Zygmund, Antoni (1988). Trigonometric Series (2nd ed.). Cambridge University Press. ISBN 978-0521358859.
See also
 |  |
