Physics:Bubble column reactor

From HandWiki
Algae bioreactor
Representation of a bubble column reactor.

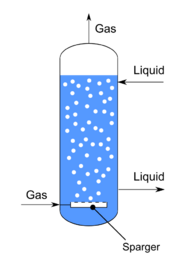
A bubble column reactor is a chemical reactor that belongs to the general class of multiphase reactors, which consists of three main categories: trickle bed reactor (fixed or packed bed), fluidized bed reactor, and bubble column reactor.[1] A bubble column reactor is a very simple device consisting of a vertical vessel filled with water with a gas distributor at the inlet. Due to the ease of design and operation, which does not involve moving parts, they are widely used in the chemical, biochemical, petrochemical, and pharmaceutical industries to generate and control gas-liquid chemical reactions.[2]

Despite the simple column arrangement, the hydrodynamics of bubble columns is very complex due to the interactions between liquid and gas phases.[3] In recent years, Computational Fluid Dynamics (CFD) has become a very popular tool to design and optimize bubble column reactors.

Technology and applications

In its simplest configuration, a bubble column consists of a vertically-arranged cylindrical column filled with liquid. The gas flow rate is introduced at the bottom of the column through a gas distributor.[1] The gas is supplied in the form of bubbles to either a liquid phase or a liquid-solid suspension. In this case, the solid particle size (typically a catalyst) ranges from 5 to 100 μm. These three-phase reactors are referred to us as slurry bubble columns.[4]

The liquid flow rate may be fed co-currently or counter-currently to the rising bubbles, or it may be zero. In the latter case, the column operates in batch condition.[1]

Bubble columns offer a significant number of advantages: excellent heat and mass transfer between the phases, low operating and maintenance costs due to the absence of moving parts, solids can be handled without any erosion or plugging problems, slow reactions can be carried out due to the high liquid residence time (this is the case for gas-liquid reactions with a Hatta number Ha <0.3), reasonable control of temperature when strongly exothermic reactions take place.[5][6] However, the back-mixing of the liquid phase (the result of buoyancy-driven recirculation) is a limitation for bubble columns: excessive back-mixing can limit the conversion efficiency. The reactor may be equipped with internals, baffles, or sieve plates, to overcome the back-mixing problem with an inevitable modification in the fluid dynamics.[7]

Bubble columns are extensively used in many industrial applications. They are of considerable interest in chemical processes involving reactions like oxidation, chlorination, alkylation, polymerization, and hydrogenation, as well as in the production of synthetic fuels via a gas conversion process ( Fischer-Tropsch process) in biochemical processes such as fermentation and biological wastewater treatment.[2]

Main applications of bubble column reactors.
Process Reactants Main products
Oxidation Ethilene

n-paraffins, cyclohexane

Acetaldehyde, secondary alcohols, adipic acid
Chlorination Aliphatic hydrocarbons,

aromatic hydrocarbons

Chlorinated compaunds
Alkylation Methanol Acetic acid
Hydroformylation Olefins Aldehydes, alcohols
Carbonylations Methanol, ethanol Acetic acid, acitic anhydride,

propionic acid

Hydrogenation Unsaturated fatty acids, glucose, nitroaromatics Saturated fatty acids, sorbitol, ammines
Gas to liquid fuels (Fischer-Tropsch) Syngas Liquid fuels
Coal liquification Coal Liquid fuels
Desulferization Petroleum fractions Desulferize fractions
Aerobic bio-chemical processes Molasses Ethanol

Hydrodynamic concepts

Due to the increasing importance of bubble column reactors in most industrial sectors, the study of their hydrodynamics acquired significant relevance in recent years. The design of bubble columns depends on the quantification of three main phenomena: (1) mixing characteristics, (2) heat and mass transfer properties, (3) chemical kinetics in case of reactants systems.[2]

As a consequence, the correct design and operation relies on the precise knowledge of the fluid dynamics phenomena on different scales: (1) molecular scale, (2) bubble scale, (3) reactor scale, and (4) industrial scale. The fluid dynamics properties in bubble columns depend on the interaction between the gas and liquid phases, which are related to the prevailing flow regime.[8]

The description of the hydrodynamics of bubble columns required the definition of some parameters. The superficial gas and liquid velocities are defined as the ratio between the volumetric flow rate of the gas and liquid, respectively, divided by the column cross-sectional area. [9] Although the superficial velocity concept is based on a simple one-dimensional flow assumption, it can be used to characterize and determine the hydrodynamics in bubble columns since an increase in its value can determine a flow regime transition. [10]

Concerning global flow properties, a fundamental aspect which is helpful in describing the bubble column design process is the global gas holdup. It is defined as the ratio of the volume occupied by the gas phase and the sum of the volume occupied by the gas and liquid phases:[3]

[math]\displaystyle{ \varepsilon_G=\frac{V_G}{V_G+V_L} }[/math]

Where:

  • [math]\displaystyle{ V_G }[/math] is the volume occupied by the gas phase.
  • [math]\displaystyle{ V_L }[/math] is the volume occupied by the liquid phase.

The gas holdup provides information about the mean residence time of bubbles inside the column. Combined with bubble dimensions ( a fundamental local flow property), it determines the interfacial area for the heat and mass transfer rate between the phases.[3]

Flow regimes in bubble columns

In multiphase reactors, the flow regime gives information about the behaviour of the gas phase and its interaction with the continuous liquid phase. The flow regime can vary significantly depending on several factors, including gas and liquid flow rates, geometric aspects of the column (column diameter, column height, sparger type, sparger holes diameter, and eventually, the size of the solid particles) and physical properties of the phases.[11]

In the most general case, four flow regimes can be encountered in bubble column reactors: (1) homogeneous or bubbly flow regime, (2) slug flow regime, (3) churn or heterogeneous flow regime, and (4) annular flow regime.[12]

Flow regimes in a vertical pipe. (a) Bubbly-homogeneous flow regime; (b) Slug flow regime; (c) Churn-heterogeneous flow regime; (d) annular flow regime.

The homogeneous flow regime takes place at very low superficial gas velocity and can be divided into mono-dispersed and poly-dispersed homogeneous flow regimes. The former is characterized by a mono-dispersed bubble size distribution, the latter by a poly-dispersed one, according to the change in sign of the lift force. Small bubbles with a positive lift coefficient move towards the column wall, and large bubbles with a negative lift coefficient move towards the column center. [13] The heterogeneous flow regime occurs at very high gas velocity and represents a chaotic and unsteady flow pattern, with high liquid recirculation and vigorous mixing. A wide range of bubble sizes is experienced, and the average bubble size is governed by coalescence and breakup phenomena, which determine the flow properties, no longer influenced by the primary bubbles generated at the sparger.

The slug and the annular flow regimes are usually observed in small-diameter bubble columns with an inner diameter of less than 0.15 m. [3] The former is characterized by giant bubbles, named Taylor bubbles, that occupy the entire cross-sectional area of the column. The latter is characterized by a central core of gas surrounded by a thin liquid film. The annular flow regime exists only at very high gas velocity.

When dealing with industrial applications, larger-diameter bubble columns are typically employed so that the slug flow regime is not usually observed due to the so-called Rayleight-Taylor instabilities.[14][15] The quantification of these instabilities at the reactor-scale is obtained by comparing the dimensionless bubble diameter, [math]\displaystyle{ D^*_H }[/math], with a critical diameter, [math]\displaystyle{ D^*_{H,cr} }[/math]: [math]\displaystyle{ D^*_H= {D_H \over \sqrt{\sigma/g(\rho_L-\rho_G)}} \gt D^*_{H,cr}=52 }[/math]

Flow regime map. (a) Slug flow regime; (b) Churn-heterogeneous flow regime; (c) Transition flow regime; (d) Bubbly-homogeneous flow regime; (α) Bubble column hydraulic diameter; (β) Superficial gas velocity.

Where [math]\displaystyle{ D_H }[/math] is the bubble column hydraulic diameter, [math]\displaystyle{ \sigma }[/math] is the surface tension, [math]\displaystyle{ g }[/math] is the acceleration due to gravity, [math]\displaystyle{ \rho_L }[/math] is the liquid phase density, and [math]\displaystyle{ \rho_G }[/math] is the gas phase density.

For example, at ambient temperature and pressure and considering air and water as working fluids, a bubble column is classified as a large-diameter if it has a hydraulic diameter greater than 0.15 m.[3]

Due to the very high gas velocity, the annular flow regime is not usually observed in industrial bubble columns. Consequently, in a large-scale bubble column, we may have only the bubbly (or homogeneous) and the churn (or heterogenous) flow regimes. Between these flow regimes, a transition region is usually observed, in which the flow field is not as distinct and well defined as in the bubbly-homogeneous and churn-heterogeneous flow regimes.[11]

The boundaries between the flow regimes can be graphically observed in the flow regimes map.

Numerical modelling

Numerical modelling of bubble column reactors is a way of predicting the multiphase flow to improve the reactor design and understand the reactor fluid dynamics. The recent increase in interest in Computational Fluid Dynamics (CFD) spurred substantial research efforts in determining numerical models that can obtain reasonably accurate predictions with limited computational time, thus overcoming the limitations of traditional empirical methods.

When a dispersed flow is considered, two main models have been developed to predict the complex fluid dynamics phenomena: the Eulerian-Lagrangian and the Eulerian-Eulerian Multi-Fluid models.[16] The Eulerian-Lagrangian model couples the Eulerian description of the continuous phase with a Lagrangian scheme for tracking the individual particulates. The dynamic of the surrounding fluid (continuous phase) is solved through the governing equations, while the particulates (dispersed phase) are tracked independently through the surrounding fluid by computing their trajectory.[17] The interactions between the phases and their impact on both the continuous and the discrete phases can be considered, but it requires a greater computational effort. Consequently, it can not be used to simulate bubble columns at the industrial scale.[8]

The Eulerian-Eulerian model considers each phase as interpenetrating continua. All the phases share a single pressure field, whereas continuity and momentum equations are solved for each phase. The coupling between the phases is achieved considering interfacial source terms.[8]

Governing equations

File:CFD simulation of a bubble column.ogg Considering an isothermal flow without mass transfer, the Unsteady Reynolds Average Navier-Stokes equations (URANS) are:[8]

[math]\displaystyle{ \frac{\partial}{\partial t}(\alpha_k\rho_k)+ \nabla\cdot(\alpha_k\rho_k\vec{u_k})=0 }[/math]

[math]\displaystyle{ \frac{\partial}{\partial t}(\alpha_k\rho_k\vec{u_k})+\nabla\cdot(\alpha_k\rho_k\vec{u_k} \vec{u_k})= -\alpha_k \nabla P+\nabla \cdot (\alpha_k \bar{\tau_k})+\alpha_k\rho_k\vec{g}+\vec{M}_{I,k} }[/math]

Where:

  • [math]\displaystyle{ \alpha_k }[/math] is the phasic volume fraction and it represents the space occupied by the k-phase.
  • [math]\displaystyle{ \rho_k }[/math] is [math]\displaystyle{ k }[/math]-phase density.
  • [math]\displaystyle{ \vec{u}_k }[/math] is the [math]\displaystyle{ k }[/math]-phase velocity.
  • P is the pressure field shared by all the phases.
  • [math]\displaystyle{ \bar{\tau}_k }[/math] is the [math]\displaystyle{ k }[/math]-phase strain stress tensor.
  • [math]\displaystyle{ g }[/math] is the acceleration due to gravity.
  • [math]\displaystyle{ \vec{M}_{I,k} }[/math] is the momentum source term.

Interfacial forces

To correctly solve the [math]\displaystyle{ k }[/math]-phase momentum equation, a feasible set of closure relations must be considered to include all the possible interactions between the phases, expressed as a momentum transfer per unit volume at the phase interface. Interfacial momentum forces are added as a source term in the momentum equation and can be divided into drag and non-drag forces. The drag force has a dominant role and can be considered as the most important contribution in bubbly flows.[18] It reflects the resistance opposing bubble motion relative to the surrounding fluid.

The non drag forces are the lift, turbulent dispersion, wall lubrication and virtual mass forces:[19]

  • Lift force: force perpendicular to bubble motion. It results from the pressure and stress acting on the bubble surface. Experimental and numerical studies show that the lift force change sign depending on the bubble diameter.[19] For small bubbles, the lift force acts in the direction of decreasing liquid velocity, which is, in the case of batch or co-current mode, toward the pipe wall. Conversely, when large bubbles are considered, the lift force pushes the bubbles toward the center of the column. The change in sign of the lift force occurs at a bubble diameter of approximately 5.8 mm.[20]
  • Turbulent dispersion: it accounts for the fluctuation in the liquid velocity that affects the dispersed phase by scattering it. The turbulent eddies redistribute the bubbles in the lateral direction from the high-concentration to the low-concentration bubble region. The turbulent dispersion force modulates the peaks of small bubbles near the wall pipes and spreads out large bubbles.[19]
  • Wall lubrication: force due to the surface tension. It prevents the bubbles from touching the walls, ensuring zero presence of bubbles near vertical walls (found experimentally).[19]
  • Virtual mass force: it arises from the relative acceleration of an immersed moving object to its surrounding fluid. Its effect is significant when the liquid phase density is much higher than the gas phase.[19]

All the interfacial forces can be added to the numerical model using suitable correlations derived from experimental studies.

Dispersed phase modelling

Depending on the regime under investigation, different approaches can be used to model the dispersed gas phase. The simplest is to use a fixed bubble size distribution. This approximation is suitable to simulate the homogeneous flow regime, where the interactions between the bubbles are negligible. In addition, this approach calls for the knowledge of the bubbles diameter since it is an input parameter for the simulations.[8]

However, in industrial practice, large-scale bubble columns are typically employed, equipped with gas distributors characterized by large openings, so a heterogeneous flow regime is commonly observed.[21] Bubble coalescence and breakup phenomena are relevant and can not be neglected. In this case, the CFD model can be coupled with a Population Balance Model (PBM) to account for the changes in bubbles size.

A Population Balance Model consists of a transport equation derived from the Boltzmann statistical transport equation, and it describes the particles entering or leaving a control volume via several mechanisms. The bubble number density transport equation is also known as Population Balance Equation (PBE):[22]

[math]\displaystyle{ \frac{\partial}{\partial t}n(\vec{x},V_b,t)+\frac{\partial}{\partial z}[n(\vec{x},V_b,t)u_b(\vec{x})] +\frac{\partial}{\partial V_b}[n(\vec{x},V_b,t)\frac{\partial}{\partial t}V_b(\vec{x},V_b)]=S(\vec{x},V_b,t) }[/math]

Where [math]\displaystyle{ n(\vec{x},V_b,t) }[/math] is the bubble number density function and represents the probable number density of bubbles at a given time [math]\displaystyle{ (t) }[/math], about a position [math]\displaystyle{ \vec{x} }[/math], with bubble volume between [math]\displaystyle{ V_b }[/math] and [math]\displaystyle{ V_b+d(V_b) }[/math], and [math]\displaystyle{ u_b }[/math] is the bubble velocity. The right and side term of the Population Balance Equation is the source/sink term due to bubbles coalescence, breakup, phase change, pressure change, mass transfer, and chemical reactions.[8]

See also

References

  1. ↑ 1.0 1.1 1.2 Leonard, C.; Ferrasse, J.-H.; Boutin, O.; Lefevre, S.; Viand, A. (August 2015). "Bubble column reactors for high pressures and high temperatures operation" (in en). Chemical Engineering Research and Design 100: 391–421. doi:10.1016/j.cherd.2015.05.013. https://linkinghub.elsevier.com/retrieve/pii/S0263876215001641. 
  2. ↑ 2.0 2.1 2.2 Kantarci, Nigar; Borak, Fahir; Ulgen, Kutlu O. (2005-06-01). "Bubble column reactors" (in en). Process Biochemistry 40 (7): 2263–2283. doi:10.1016/j.procbio.2004.10.004. ISSN 1359-5113. https://www.sciencedirect.com/science/article/pii/S0032959204004418. 
  3. ↑ 3.0 3.1 3.2 3.3 3.4 Besagni, Giorgio (2021-02-01). "Bubble column fluid dynamics: A novel perspective for flow regimes and comprehensive experimental investigations" (in en). International Journal of Multiphase Flow 135: 103510. doi:10.1016/j.ijmultiphaseflow.2020.103510. ISSN 0301-9322. https://www.sciencedirect.com/science/article/pii/S0301932220306212. 
  4. ↑ Krishna, Rajamani; De Swart, Jeroen W. A.; Ellenberger, Jürg; Martina, Gilbert B.; Maretto, Cristina (February 1997). "Gas holdup in slurry bubble columns: Effect of column diameter and slurry concentrations" (in en). AIChE Journal 43 (2): 311–316. doi:10.1002/aic.690430204. ISSN 0001-1541. https://onlinelibrary.wiley.com/doi/10.1002/aic.690430204. 
  5. ↑ Shaikh, Ashfaq; Al-Dahhan, Muthanna H. (2007-08-19). "A Review on Flow Regime Transition in Bubble Columns" (in en). International Journal of Chemical Reactor Engineering 5 (1). doi:10.2202/1542-6580.1368. ISSN 1542-6580. https://www.degruyter.com/document/doi/10.2202/1542-6580.1368/html. 
  6. ↑ Rollbusch, Philipp; Bothe, Melanie; Becker, Marc; Ludwig, Martina; Grünewald, Marcus; Schlüter, Michael; Franke, Robert (2015-04-14). "Bubble columns operated under industrially relevant conditions – Current understanding of design parameters" (in en). Chemical Engineering Science 126: 660–678. doi:10.1016/j.ces.2014.11.061. ISSN 0009-2509. Bibcode: 2015ChEnS.126..660R. https://www.sciencedirect.com/science/article/pii/S0009250914007362. 
  7. ↑ Degaleesan, S.; Dudukovic, M.; Pan, Y. (September 2001). "Experimental study of gas-induced liquid-flow structures in bubble columns" (in en). AIChE Journal 47 (9): 1913–1931. doi:10.1002/aic.690470904. https://onlinelibrary.wiley.com/doi/10.1002/aic.690470904. 
  8. ↑ 8.0 8.1 8.2 8.3 8.4 8.5 Besagni, Giorgio; Inzoli, Fabio; Ziegenhein, Thomas (June 2018). "Two-Phase Bubble Columns: A Comprehensive Review" (in en). ChemEngineering 2 (2): 13. doi:10.3390/chemengineering2020013. ISSN 2305-7084. 
  9. ↑ Crowe, Clayton T. (2006). Multiphase flow handbook. Taylor & Francis. pp. 1–3. ISBN 978-1-4200-4047-0. 
  10. ↑ Li, Tingwen; Grace, John; Shadle, Lawrence; Guenther, Chris (2011-11-15). "On the superficial gas velocity in deep gas–solids fluidized beds" (in en). Chemical Engineering Science 66 (22): 5735–5738. doi:10.1016/j.ces.2011.08.002. ISSN 0009-2509. Bibcode: 2011ChEnS..66.5735L. https://www.sciencedirect.com/science/article/pii/S0009250911005550. 
  11. ↑ 11.0 11.1 Krishna, R.; Ellenberger, J.; Maretto, C. (1999-05-01). "Flow regime transition in bubble columns" (in en). International Communications in Heat and Mass Transfer 26 (4): 467–475. doi:10.1016/S0735-1933(99)00032-9. ISSN 0735-1933. https://www.sciencedirect.com/science/article/pii/S0735193399000329. 
  12. ↑ Shaikh, Ashfaq; Al-Dahhan, Muthanna H. (2007-08-19). "A Review on Flow Regime Transition in Bubble Columns" (in en). International Journal of Chemical Reactor Engineering 5 (1). doi:10.2202/1542-6580.1368. ISSN 1542-6580. https://www.degruyter.com/document/doi/10.2202/1542-6580.1368/html. 
  13. ↑ Lucas, D.; Prasser, H. -M.; Manera, A. (2005-07-01). "Influence of the lift force on the stability of a bubble column" (in en). Chemical Engineering Science 60 (13): 3609–3619. doi:10.1016/j.ces.2005.02.032. ISSN 0009-2509. Bibcode: 2005ChEnS..60.3609L. https://www.sciencedirect.com/science/article/pii/S0009250905001326. 
  14. ↑ Didwania, Anjani K.; Homsy, G. M. (November 1981). "Rayleigh-Taylor instabilities in fluidized beds" (in en). Industrial & Engineering Chemistry Fundamentals 20 (4): 318–323. doi:10.1021/i100004a003. ISSN 0196-4313. https://pubs.acs.org/doi/abs/10.1021/i100004a003. 
  15. ↑ Kitscha, J.; Kocamustafaogullari, G. (1989-07-01). "Breakup criteria for fluid particles" (in en). International Journal of Multiphase Flow 15 (4): 573–588. doi:10.1016/0301-9322(89)90054-2. ISSN 0301-9322. https://dx.doi.org/10.1016/0301-9322%2889%2990054-2. 
  16. ↑ Jadhav, Ananda J.; Barigou, Mostafa (2022-10-01). "Eulerian-Lagrangian Modelling of Turbulent Two-Phase Particle-Liquid Flow in a Stirred Vessel: CFD and Experiments Compared" (in en). International Journal of Multiphase Flow 155: 104191. doi:10.1016/j.ijmultiphaseflow.2022.104191. ISSN 0301-9322. https://www.sciencedirect.com/science/article/pii/S0301932222001732. 
  17. ↑ Simonnet, M.; Gentric, C.; Olmos, E.; Midoux, N. (2008-09-01). "CFD simulation of the flow field in a bubble column reactor: Importance of the drag force formulation to describe regime transitions" (in en). Chemical Engineering and Processing: Process Intensification 47 (9): 1726–1737. doi:10.1016/j.cep.2007.08.015. ISSN 0255-2701. https://www.sciencedirect.com/science/article/pii/S025527010700308X. 
  18. ↑ Tabib, Mandar V.; Roy, Swarnendu A.; Joshi, Jyeshtharaj B. (2008-06-15). "CFD simulation of bubble column—An analysis of interphase forces and turbulence models" (in en). Chemical Engineering Journal 139 (3): 589–614. doi:10.1016/j.cej.2007.09.015. ISSN 1385-8947. https://www.sciencedirect.com/science/article/pii/S1385894707006201. 
  19. ↑ 19.0 19.1 19.2 19.3 19.4 Ziegenhein, T.; Rzehak, R.; Lucas, D. (2015-01-27). "Transient simulation for large scale flow in bubble columns" (in en). Chemical Engineering Science 122: 1–13. doi:10.1016/j.ces.2014.09.022. ISSN 0009-2509. Bibcode: 2015ChEnS.122....1Z. https://www.sciencedirect.com/science/article/pii/S0009250914005260. 
  20. ↑ Tomiyama, Akio; Tamai, Hidesada; Zun, Iztok; Hosokawa, Shigeo (2002-06-01). "Transverse migration of single bubbles in simple shear flows" (in en). Chemical Engineering Science 57 (11): 1849–1858. doi:10.1016/S0009-2509(02)00085-4. ISSN 0009-2509. Bibcode: 2002ChEnS..57.1849T. https://www.sciencedirect.com/science/article/pii/S0009250902000854. 
  21. ↑ Im, Hanjin; Park, Jeil; Lee, Jae W. (2019-01-31). "Prediction of Main Regime Transition with Variations of Gas and Liquid Phases in a Bubble Column" (in en). ACS Omega 4 (1): 1329–1343. doi:10.1021/acsomega.8b02657. ISSN 2470-1343. PMID 31459402. 
  22. ↑ Liao, Yixiang; Lucas, Dirk (2010-05-15). "A literature review on mechanisms and models for the coalescence process of fluid particles" (in en). Chemical Engineering Science 65 (10): 2851–2864. doi:10.1016/j.ces.2010.02.020. ISSN 0009-2509. https://www.sciencedirect.com/science/article/pii/S000925091000093X. 


External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Bubble_column_reactor&oldid=3417030"