Physics:Characteristic mode analysis

From HandWiki

Characteristic modes (CM) form a set of functions which, under specific boundary conditions, diagonalizes operator relating field and induced sources. Under certain conditions, the set of the CM is unique and complete (at least theoretically) and thereby capable of describing the behavior of a studied object in full. This article deals with characteristic mode decomposition in electromagnetics, a domain in which the CM theory has originally been proposed.

Background

CM decomposition was originally introduced as set of modes diagonalizing a scattering matrix.[1][2] The theory has, subsequently, been generalized by Harrington and Mautz for antennas.[3][4] Harrington, Mautz and their students also successively developed several other extensions of the theory.[5][6][7][8] Even though some precursors[9] were published back in the late 1940s, the full potential of CM has remained unrecognized for an additional 40 years. The capabilities of CM were revisited[10] in 2007 and, since then, interest in CM has dramatically increased. The subsequent boom of CM theory is reflected by the number of prominent publications and applications.

Definition

For simplicity, only the original form of the CM – formulated for perfectly electrically conducting (PEC) bodies in free space — will be treated in this article. The electromagnetic quantities will solely be represented as Fourier's images in frequency domain. Lorenz's gauge is used.

Example of a scatterer [math]\displaystyle{ \Omega }[/math] composed of a perfect electric conductor.

The scattering of an electromagnetic wave on a PEC body is represented via a boundary condition on the PEC body, namely

[math]\displaystyle{ \boldsymbol{\hat{n}} \times \boldsymbol{E}^\mathrm{i} = -\boldsymbol{\hat{n}} \times \boldsymbol{E}^\mathrm{s}, }[/math]

with [math]\displaystyle{ \boldsymbol{\hat{n}} }[/math] representing unitary normal to the PEC surface, [math]\displaystyle{ \boldsymbol{E}^\mathrm{i} }[/math] representing incident electric field intensity, and [math]\displaystyle{ \boldsymbol{E}^\mathrm{s} }[/math] representing scattered electric field intensity defined as

[math]\displaystyle{ \boldsymbol{E}^\mathrm{s} = -\mathrm{j}\omega\boldsymbol{A} - \nabla\varphi, }[/math]

with [math]\displaystyle{ \mathrm{j} }[/math] being imaginary unit, [math]\displaystyle{ \omega }[/math] being angular frequency, [math]\displaystyle{ \boldsymbol{A} }[/math] being vector potential

[math]\displaystyle{ \boldsymbol{A} \left(\boldsymbol{r}\right) = \mu_0 \int\limits_\Omega \boldsymbol{J} \left(\boldsymbol{r}'\right) G \left(\boldsymbol{r}, \boldsymbol{r}'\right) \, \mathrm{d}S, }[/math]

[math]\displaystyle{ \mu_0 }[/math] being vacuum permeability, [math]\displaystyle{ \varphi }[/math] being scalar potential

[math]\displaystyle{ \varphi \left(\boldsymbol{r}\right) = - \frac{1}{\mathrm{j}\omega\epsilon_0} \int\limits_\Omega \nabla\cdot\boldsymbol{J} \left(\boldsymbol{r}'\right) G \left(\boldsymbol{r}, \boldsymbol{r}'\right) \, \mathrm{d}S, }[/math]

[math]\displaystyle{ \epsilon_0 }[/math] being vacuum permittivity, [math]\displaystyle{ G \left(\boldsymbol{r},\boldsymbol{r}'\right) }[/math] being scalar Green's function

[math]\displaystyle{ G \left(\boldsymbol{r},\boldsymbol{r}'\right) = \frac{\mathrm{e}^{-\mathrm{j}k\left|\boldsymbol{r} - \boldsymbol{r}'\right|}}{4\pi \left|\boldsymbol{r} - \boldsymbol{r}'\right|} }[/math]

and [math]\displaystyle{ k }[/math] being wavenumber. The integro-differential operator [math]\displaystyle{ \boldsymbol{\hat{n}} \times \boldsymbol{E}^\mathrm{s} \left(\boldsymbol{J} \right) }[/math] is the one to be diagonalized via characteristic modes.

The governing equation of the CM decomposition is

[math]\displaystyle{ \mathcal{X} \left(\boldsymbol{J}_n\right) = \lambda_n \mathcal{R} \left(\boldsymbol{J}_n\right) \qquad\mathrm{(1)} }[/math]

with [math]\displaystyle{ \mathcal{R} }[/math] and [math]\displaystyle{ \mathcal{X} }[/math] being real and imaginary parts of impedance operator, respectively: [math]\displaystyle{ \mathcal{Z}(\cdot) = \mathcal{R}(\cdot) + \mathrm{j}\mathcal{X}(\cdot)\,. }[/math] The operator, [math]\displaystyle{ \mathcal{Z} }[/math] is defined by

[math]\displaystyle{ \mathcal{Z} \left(\boldsymbol{J}\right) = \boldsymbol{\hat{n}} \times \boldsymbol{\hat{n}} \times \boldsymbol{E}^\mathrm{s} \left(\boldsymbol{J}\right). \qquad\mathrm{(2)} }[/math]

The outcome of (1) is a set of characteristic modes [math]\displaystyle{ \left\{\boldsymbol{J}_n\right\} }[/math], [math]\displaystyle{ n\in \left\{1,2,\dots\right\} }[/math], accompanied by associated characteristic numbers [math]\displaystyle{ \left\{\lambda_n\right\} }[/math]. Clearly, (1) is a generalized eigenvalue problem, which, however, cannot be analytically solved (except for a few canonical bodies[11]). Therefore, the numerical solution described in the following paragraph is commonly employed.

Matrix formulation

Discretization [math]\displaystyle{ \mathcal{D} }[/math] of the body of the scatterer [math]\displaystyle{ \Omega }[/math] into [math]\displaystyle{ M }[/math] subdomains as [math]\displaystyle{ \Omega^M = \mathcal{D}\left(\Omega\right) }[/math] and using a set of linearly independent piece-wise continuous functions [math]\displaystyle{ \left\{\boldsymbol{\psi}_n\right\} }[/math], [math]\displaystyle{ n\in\left\{1,\dots,N\right\} }[/math], allows current density [math]\displaystyle{ \boldsymbol{J} }[/math] to be represented as

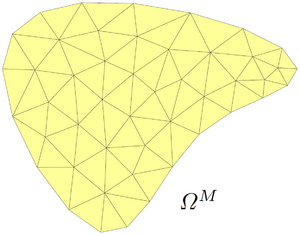
Example of a scatterer's triangular (Delaunay) discretization [math]\displaystyle{ \Omega^M }[/math].
[math]\displaystyle{ \boldsymbol{J} \left(\boldsymbol{r}\right) \approx \sum\limits_{n=1}^N I_n \boldsymbol{\psi}_n \left(\boldsymbol{r}\right) }[/math]

and by applying the Galerkin method, the impedance operator (2)

[math]\displaystyle{ \mathbf{Z} = \mathbf{R} + \mathrm{j} \mathbf{X} = \left[Z_{uv}\right] = \left[\,\int\limits_\Omega \boldsymbol{\psi}_u^\ast \cdot \mathcal{Z} \left(\boldsymbol{\psi}_v\right) \, \mathrm{d}S\right]. }[/math]

The eigenvalue problem (1) is then recast into its matrix form

[math]\displaystyle{ \mathbf{X} \mathbf{I}_n = \lambda_n \mathbf{R}\mathbf{I}_n, }[/math]

which can easily be solved using, e.g., the generalized Schur decomposition or the implicitly restarted Arnoldi method yielding a finite set of expansion coefficients [math]\displaystyle{ \left\{\mathbf{I}_n\right\} }[/math] and associated characteristic numbers [math]\displaystyle{ \left\{\lambda_n\right\} }[/math]. The properties of the CM decomposition are investigated below.

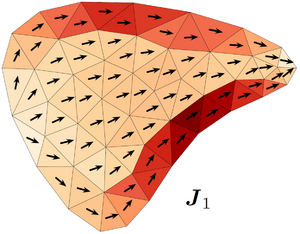
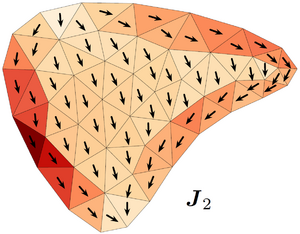
The first (dominant) characteristic mode of a shape [math]\displaystyle{ \Omega^M }[/math].
The second characteristic mode of a shape [math]\displaystyle{ \Omega^M }[/math].

Properties

The properties of CM decomposition are demonstrated in its matrix form.

First, recall that the bilinear forms

[math]\displaystyle{ P_\mathrm{r} \approx \frac{1}{2} \mathbf{I}^\mathrm{H} \mathbf{R} \mathbf{I} \geq 0 }[/math]

and

[math]\displaystyle{ 2\omega\left(W_\mathrm{m} - W_\mathrm{e}\right) \approx \frac{1}{2} \mathbf{I}^\mathrm{H} \mathbf{X} \mathbf{I}, }[/math]

where superscript [math]\displaystyle{ ^\mathrm{H} }[/math] denotes the Hermitian transpose and where [math]\displaystyle{ \mathbf{I} }[/math] represents an arbitrary surface current distribution, correspond to the radiated power and the reactive net power,[12] respectively. The following properties can then be easily distilled:

  • The weighting matrix [math]\displaystyle{ \mathbf{R} }[/math] is theoretically positive definite and [math]\displaystyle{ \mathbf{X} }[/math] is indefinite. The Rayleigh quotient
[math]\displaystyle{ \lambda_n \approx \frac{\mathbf{I}_n^\mathrm{H}\mathbf{X}\mathbf{I}_n}{\mathbf{I}_n^\mathrm{H}\mathbf{R}\mathbf{I}_n} }[/math]

then spans the range of [math]\displaystyle{ -\infty \leq \lambda_n \leq \infty }[/math] and indicates whether the characteristic mode is capacitive ([math]\displaystyle{ \lambda_n \lt 0 }[/math]), inductive ([math]\displaystyle{ \lambda_n \gt 0 }[/math]), or in resonance ([math]\displaystyle{ \lambda_n = 0 }[/math]). In reality, the Rayleigh quotient is limited by the numerical dynamics of the machine precision used and the number of correctly found modes is limited.

  • The characteristic numbers evolve with frequency, i.e., [math]\displaystyle{ \lambda_n = \lambda_n \left(\omega\right) }[/math], they can cross each other, or they can be the same (in case of degeneracies[13]). For this reason, the tracking of modes is often applied to get smooth curves [math]\displaystyle{ \lambda_n \left(\omega\right) }[/math].[14][15][16][17][18] Unfortunately, this process is partly heuristic and the tracking algorithms are still far from perfection.[11]
  • The characteristic modes can be chosen as real-valued functions, [math]\displaystyle{ \mathbf{I}_n \in \mathbb{R}^{N\times 1} }[/math]. In other words, characteristic modes form a set of equiphase currents.
  • The CM decomposition is invariant with respect to the amplitude of the characteristic modes. This fact is used to normalize the current so that they radiate unitary radiated power
[math]\displaystyle{ \frac{1}{2} \mathbf{I}_m^\mathrm{H} \mathbf{Z} \mathbf{I}_n \approx \left(1 + \mathrm{j} \lambda_n\right) \delta_{mn}. }[/math]

This last relation presents the ability of characteristic modes to diagonalize the impedance operator (2) and demonstrates far field orthogonality, i.e.,

[math]\displaystyle{ \frac{1}{2} \sqrt{\frac{\varepsilon_0}{\mu_0}} \int\limits_0^{2\pi} \int\limits_0^\pi \boldsymbol{F}_m^\ast \cdot \boldsymbol{F}_n \sin \vartheta \, \mathrm{d} \vartheta \, \mathrm{d} \varphi = \delta_{mn}. }[/math]

Modal quantities

The modal currents can be used to evaluate antenna parameters in their modal form, for example:

  • modal far-field [math]\displaystyle{ \boldsymbol{F}_n \left(\boldsymbol{\hat{e}}, \boldsymbol{\hat{r}}\right) }[/math] ([math]\displaystyle{ \boldsymbol{\hat{e}} }[/math] — polarization, [math]\displaystyle{ \boldsymbol{\hat{r}} }[/math] — direction),[3]
  • modal directivity [math]\displaystyle{ \boldsymbol{D}_n \left(\boldsymbol{\hat{e}}, \boldsymbol{\hat{r}}\right) }[/math],
  • modal radiation efficiency [math]\displaystyle{ \eta_n }[/math],[19]
  • modal quality factor [math]\displaystyle{ Q_n }[/math],[20]
  • modal impedance [math]\displaystyle{ Z_n }[/math].

These quantities can be used for analysis, feeding synthesis, radiator's shape optimization, or antenna characterization.

Applications and further development

The number of potential applications is enormous and still growing:

The prospective topics include

  • electrically large structures calculated using MLFMA,[38]
  • dielectrics,[7][39]
  • use of Combined Field Integral Equation,[40]
  • periodic structures,
  • formulation for arrays.[41]

Software

CM decomposition has recently been implemented in major electromagnetic simulators, namely in FEKO,[42] CST-MWS,[43] and WIPL-D.[44] Other packages are about to support it soon, for example HFSS[45] and CEM One.[46] In addition, there is a plethora of in-house and academic packages which are capable of evaluating CM and many associated parameters.

Alternative bases

CM are useful to understand radiator's operation better. They have been used with great success for many practical purposes. However, it is important to stress that they are not perfect and it is often better to use other formulations such as energy modes,[47] radiation modes,[47] stored energy modes[32] or radiation efficiency modes.[48]

References

  1. ↑ Garbacz, R.J. (1965). "Modal expansions for resonance scattering phenomena". Proceedings of the IEEE 53 (8): 856–864. doi:10.1109/proc.1965.4064. ISSN 0018-9219. 
  2. ↑ Garbacz, R. J., "A Generalized Expansion for Radiated and Scattered Fields," PhD thesis, Department of Electrical Engineering, The Ohio State Univ., 1968.
  3. ↑ 3.0 3.1 Harrington, R.; Mautz, J. (1971). "Theory of characteristic modes for conducting bodies". IEEE Transactions on Antennas and Propagation 19 (5): 622–628. doi:10.1109/tap.1971.1139999. ISSN 0096-1973. Bibcode: 1971ITAP...19..622H. 
  4. ↑ Harrington, R.; Mautz, J. (1971). "Computation of characteristic modes for conducting bodies". IEEE Transactions on Antennas and Propagation 19 (5): 629–639. doi:10.1109/tap.1971.1139990. ISSN 0096-1973. Bibcode: 1971ITAP...19..629H. 
  5. ↑ Chang, Y.; Harrington, R. (1977). "A surface formulation for characteristic modes of material bodies". IEEE Transactions on Antennas and Propagation 25 (6): 789–795. doi:10.1109/tap.1977.1141685. ISSN 0096-1973. Bibcode: 1977ITAP...25..789C. 
  6. ↑ Harrington, R.F.; Mautz, J.R. (1985). "Characteristic Modes for Aperture Problems". IEEE Transactions on Microwave Theory and Techniques 33 (6): 500–505. doi:10.1109/tmtt.1985.1133105. ISSN 0018-9480. Bibcode: 1985ITMTT..33..500H. 
  7. ↑ 7.0 7.1 Harrington, R. F.; Mautz, J.R.; Chang, Y. (March 1972). "Characteristic modes for dielectric and magnetic bodies". IEEE Transactions on Antennas and Propagation 20 (2): 194–198. doi:10.1109/TAP.1972.1140154. Bibcode: 1972ITAP...20..194H. 
  8. ↑ El-Hajj, A.; Kabalan, K.Y.; Harrington, R.F. (1993). "Characteristic mode analysis off electromagnetic coupling through multiple slots in a conducting plane". IEE Proceedings H - Microwaves, Antennas and Propagation 140 (6): 421. doi:10.1049/ip-h-2.1993.0069. ISSN 0950-107X. 
  9. ↑ Montgomery, C. G.; Dicke, R.H.; Purcell, E. M., Principles of Microwave Circuits, Section 9.24, New York, United States: McGraw-Hill, 1948.
  10. ↑ Cabedo-Fabres, Marta; Antonino-Daviu, Eva; Valero-Nogueira, Alejandro; Bataller, Miguel (2007). "The Theory of Characteristic Modes Revisited: A Contribution to the Design of Antennas for Modern Applications". IEEE Antennas and Propagation Magazine 49 (5): 52–68. doi:10.1109/map.2007.4395295. ISSN 1045-9243. Bibcode: 2007IAPM...49...52C. 
  11. ↑ 11.0 11.1 11.2 Capek, Miloslav; Losenicky, Vit; Jelinek, Lukas; Gustafsson, Mats (2017). "Validating the Characteristic Modes Solvers". IEEE Transactions on Antennas and Propagation 65 (8): 4134–4145. doi:10.1109/tap.2017.2708094. ISSN 0018-926X. Bibcode: 2017ITAP...65.4134C. 
  12. ↑ Harrington, R. F., Field Computation by Moment Methods, Wiley -- IEEE Press, 1993.
  13. ↑ Schab, K. R.; Bernhard, J. T. (2017). "A Group Theory Rule for Predicting Eigenvalue Crossings in Characteristic Mode Analyses". IEEE Antennas and Wireless Propagation Letters 16: 944–947. doi:10.1109/lawp.2016.2615041. ISSN 1536-1225. Bibcode: 2017IAWPL..16..944S. 
  14. ↑ Capek, Miloslav; Hazdra, Pavel; Hamouz, Pavel; Eichler, Jan (2011). "A method for tracking characteristic numbers and vectors". Progress in Electromagnetics Research B 33: 115–134. doi:10.2528/pierb11060209. ISSN 1937-6472. 
  15. ↑ Raines, Bryan D.; Rojas, Roberto G. (2012). "Wideband Characteristic Mode Tracking". IEEE Transactions on Antennas and Propagation 60 (7): 3537–3541. doi:10.1109/tap.2012.2196914. ISSN 0018-926X. Bibcode: 2012ITAP...60.3537R. 
  16. ↑ Ludick, D.J.; Jakobus, U.; Vogel, M. (2014). "A tracking algorithm for the eigenvectors calculated with characteristic mode analysis". Proceedings of the 8th European Conference on Antennas and Propagation. IEEE. pp. 569–572. doi:10.1109/eucap.2014.6901820. ISBN 978-88-907018-4-9. 
  17. ↑ Miers, Zachary; Lau, Buon Kiong (2015). "Wideband Characteristic Mode Tracking Utilizing Far-Field Patterns". IEEE Antennas and Wireless Propagation Letters 14: 1658–1661. doi:10.1109/lawp.2015.2417351. ISSN 1536-1225. Bibcode: 2015IAWPL..14.1658M. http://lup.lub.lu.se/record/5205508. 
  18. ↑ Safin, Eugen; Manteuffel, Dirk (2016). "Advanced Eigenvalue Tracking of Characteristic Modes". IEEE Transactions on Antennas and Propagation 64 (7): 2628–2636. doi:10.1109/tap.2016.2556698. ISSN 0018-926X. Bibcode: 2016ITAP...64.2628S. 
  19. ↑ Capek, Miloslav; Hazdra, Pavel; Eichler, Jan (9 January 2015). "Evaluating radiation efficiency from characteristic currents". IET Microwaves, Antennas & Propagation 9 (1): 10–15. doi:10.1049/iet-map.2013.0473. ISSN 1751-8725. 
  20. ↑ Capek, Miloslav; Hazdra, Pavel; Eichler, Jan (2012). "A Method for the Evaluation of Radiation Q Based on Modal Approach". IEEE Transactions on Antennas and Propagation 60 (10): 4556–4567. doi:10.1109/tap.2012.2207329. ISSN 0018-926X. Bibcode: 2012ITAP...60.4556C. 
  21. ↑ Wu, Qi; Su, Donglin (2013). "A Broadband Model of the Characteristic Currents for Rectangular Plates". IEEE Transactions on Electromagnetic Compatibility 55 (4): 725–732. doi:10.1109/temc.2012.2221718. ISSN 0018-9375. 
  22. ↑ Vogel, Martin; Gampala, Gopinath; Ludick, Danie; Reddy, C.J. (2015). "Characteristic Mode Analysis: Putting Physics back into Simulation". IEEE Antennas and Propagation Magazine 57 (2): 307–317. doi:10.1109/map.2015.2414670. ISSN 1045-9243. Bibcode: 2015IAPM...57..307V. 
  23. ↑ Yang, Binbin; Adams, Jacob J. (2016). "Computing and Visualizing the Input Parameters of Arbitrary Planar Antennas via Eigenfunctions". IEEE Transactions on Antennas and Propagation 64 (7): 2707–2718. doi:10.1109/tap.2016.2554604. ISSN 0018-926X. Bibcode: 2016ITAP...64.2707Y. 
  24. ↑ Li, Hui; Miers, Zachary Thomas; Lau, Buon Kiong (2014). "Design of Orthogonal MIMO Handset Antennas Based on Characteristic Mode Manipulation at Frequency Bands Below 1 GHz". IEEE Transactions on Antennas and Propagation 62 (5): 2756–2766. doi:10.1109/tap.2014.2308530. ISSN 0018-926X. Bibcode: 2014ITAP...62.2756L. http://portal.research.lu.se/ws/files/42807229/li_tap2014.pdf. 
  25. ↑ Deng, Changjiang; Feng, Zhenghe; Hum, Sean Victor (2016). "MIMO Mobile Handset Antenna Merging Characteristic Modes for Increased Bandwidth". IEEE Transactions on Antennas and Propagation 64 (7): 2660–2667. doi:10.1109/tap.2016.2537358. ISSN 0018-926X. Bibcode: 2016ITAP...64.2660D. 
  26. ↑ Yang, Binbin; Adams, Jacob J. (2016). "Systematic Shape Optimization of Symmetric MIMO Antennas Using Characteristic Modes". IEEE Transactions on Antennas and Propagation 64 (7): 2668–2678. doi:10.1109/tap.2015.2473703. ISSN 0018-926X. Bibcode: 2016ITAP...64.2668Y. 
  27. ↑ Eichler, J.; Hazdra, P.; Capek, M.; Korinek, T.; Hamouz, P. (2011). "Design of a Dual-Band Orthogonally Polarized L-Probe-Fed Fractal Patch Antenna Using Modal Methods". IEEE Antennas and Wireless Propagation Letters 10: 1389–1392. doi:10.1109/lawp.2011.2178811. ISSN 1536-1225. Bibcode: 2011IAWPL..10.1389E. 
  28. ↑ Rezaiesarlak, Reza; Manteghi, Majid (2015). "Design of Chipless RFID Tags Based on Characteristic Mode Theory (CMT)". IEEE Transactions on Antennas and Propagation 63 (2): 711–718. doi:10.1109/tap.2014.2382640. ISSN 0018-926X. Bibcode: 2015ITAP...63..711R. 
  29. ↑ Bohannon, Nicole L.; Bernhard, Jennifer T. (2015). "Design Guidelines Using Characteristic Mode Theory for Improving the Bandwidth of PIFAs". IEEE Transactions on Antennas and Propagation 63 (2): 459–465. doi:10.1109/tap.2014.2374213. ISSN 0018-926X. Bibcode: 2015ITAP...63..459B. 
  30. ↑ Chen, Yikai; Wang, Chao-Fu (2014). "Electrically Small UAV Antenna Design Using Characteristic Modes". IEEE Transactions on Antennas and Propagation 62 (2): 535–545. doi:10.1109/tap.2013.2289999. ISSN 0018-926X. Bibcode: 2014ITAP...62..535C. 
  31. ↑ Austin, B.A.; Murray, K.P. (1998). "The application of characteristic-mode techniques to vehicle-mounted NVIS antennas". IEEE Antennas and Propagation Magazine 40 (1): 7–21. doi:10.1109/74.667319. ISSN 1045-9243. Bibcode: 1998IAPM...40....7A. 
  32. ↑ 32.0 32.1 Gustafsson, M.; Tayli, D.; Ehrenborg, C.; Cismasu, M.; Norbedo, S. (May–June 2016). "Antenna current optimization using MATLAB and CVX". FERMAT 15: 1–29. https://www.e-fermat.org/articles/gustafsson-art-2016-vol15-may-jun-005/. 
  33. ↑ Adams, Jacob J.; Bernhard, Jennifer T. (2013). "Broadband Equivalent Circuit Models for Antenna Impedances and Fields Using Characteristic Modes". IEEE Transactions on Antennas and Propagation 61 (8): 3985–3994. doi:10.1109/tap.2013.2261852. ISSN 0018-926X. Bibcode: 2013ITAP...61.3985A. 
  34. ↑ Safin, Eugen; Manteuffel, Dirk (2015). "Manipulation of Characteristic Wave Modes by Impedance Loading". IEEE Transactions on Antennas and Propagation 63 (4): 1756–1764. doi:10.1109/tap.2015.2401586. ISSN 0018-926X. Bibcode: 2015ITAP...63.1756S. 
  35. ↑ Hassan, Ahmed M.; Vargas-Lara, Fernando; Douglas, Jack F.; Garboczi, Edward J. (2016). "Electromagnetic Resonances of Individual Single-Walled Carbon Nanotubes With Realistic Shapes: A Characteristic Modes Approach". IEEE Transactions on Antennas and Propagation 64 (7): 2743–2757. doi:10.1109/tap.2016.2526046. ISSN 0018-926X. Bibcode: 2016ITAP...64.2743H. 
  36. ↑ Rabah, M. Hassanein; Seetharamdoo, Divitha; Berbineau, Marion (2016). "Analysis of Miniature Metamaterial and Magnetodielectric Arbitrary-Shaped Patch Antennas Using Characteristic Modes: Evaluation of the $Q$ Factor". IEEE Transactions on Antennas and Propagation 64 (7): 2719–2731. doi:10.1109/tap.2016.2571723. ISSN 0018-926X. Bibcode: 2016ITAP...64.2719R. 
  37. ↑ Rabah, M. Hassanein; Seetharamdoo, Divitha; Berbineau, Marion; De Lustrac, Andre (2016). "New Metrics for Artificial Magnetism From Metal-Dielectric Metamaterial Based on the Theory of Characteristic Modes". IEEE Antennas and Wireless Propagation Letters 15: 460–463. doi:10.1109/lawp.2015.2452269. ISSN 1536-1225. Bibcode: 2016IAWPL..15..460R. 
  38. ↑ Dai, Qi I.; Wu, Junwei; Gan, Hui; Liu, Qin S.; Chew, Weng Cho; Sha, Wei E. I. (2016). "Large-Scale Characteristic Mode Analysis With Fast Multipole Algorithms". IEEE Transactions on Antennas and Propagation 64 (7): 2608–2616. doi:10.1109/tap.2016.2526083. ISSN 0018-926X. Bibcode: 2016ITAP...64.2608D. 
  39. ↑ Guo, Liwen; Chen, Yikai; Yang, Shiwen (2017). "Characteristic Mode Formulation for Dielectric Coated Conducting Bodies". IEEE Transactions on Antennas and Propagation 65 (3): 1248–1258. doi:10.1109/tap.2016.2647687. ISSN 0018-926X. Bibcode: 2017ITAP...65.1248G. 
  40. ↑ Dai, Qi I.; Liu, Qin S.; Gan, Hui U. I.; Chew, Weng Cho (2015). "Combined Field Integral Equation-Based Theory of Characteristic Mode". IEEE Transactions on Antennas and Propagation 63 (9): 3973–3981. doi:10.1109/tap.2015.2452938. ISSN 0018-926X. Bibcode: 2015ITAP...63.3973D. 
  41. ↑ Tzanidis, Ioannis; Sertel, Kubilay; Volakis, John L. (2012). "Characteristic Excitation Taper for Ultrawideband Tightly Coupled Antenna Arrays". IEEE Transactions on Antennas and Propagation 60 (4): 1777–1784. doi:10.1109/tap.2012.2186269. ISSN 0018-926X. Bibcode: 2012ITAP...60.1777T. 
  42. ↑ Altair, FEKO, 2017.
  43. ↑ Dassault Systemes, CST Computer Simulation Technology, [Online: CST-MWS, 2017.
  44. ↑ WIPL-D d.o.o., [Online: WIPL-D, 2017.
  45. ↑ ANSYS, [Online: HFSS, 2017.
  46. ↑ ESI Group, [Online: CEM One, 2017.
  47. ↑ 47.0 47.1 Schab, Kurt R.; Bernhard, Jennifer T. (2015). "Radiation and Energy Storage Current Modes on Conducting Structures". IEEE Transactions on Antennas and Propagation 63 (12): 5601–5611. doi:10.1109/tap.2015.2490664. ISSN 0018-926X. Bibcode: 2015ITAP...63.5601S. 
  48. ↑ Jelinek, Lukas; Capek, Miloslav (2017). "Optimal Currents on Arbitrarily Shaped Surfaces". IEEE Transactions on Antennas and Propagation 65 (1): 329–341. doi:10.1109/tap.2016.2624735. ISSN 0018-926X. Bibcode: 2017ITAP...65..329J. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Characteristic_mode_analysis&oldid=3280389"